I have two postscripts to my American Scientist column on memristors and the related posting here on bit-player.
First up is a charming preprint by Yuriy V. Pershin and Massimiliano Di Ventra on “Solving mazes with memristors: a massively-parallel approach.” The moment I saw the title, I guessed the basic idea behind this work—and I was half right.
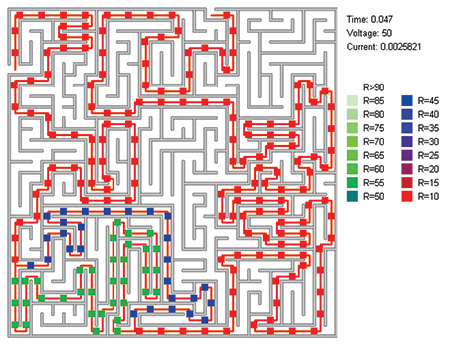
The part I got right is that you fill the maze with a network of memristors, wiring them together along the corridors but making no connections that cross walls; then you apply a voltage between the entrance and the exit nodes. Current flows only through those nodes that lie along the solution path; there’s no current in any of the dead-end branches. The current passing through the memristors along the path alters their resistance, creating a permanent record of the solution.
But there’s a complication I missed. A memristor is a polar device: In one direction, current decreases the resistance; but when current flows the other way, the resistance increases. This wouldn’t be a problem if you could just arrange the memristors so that all of them on the solution path are oriented the same way—but if you knew enough to do that, you’d already know a great deal about the solution. Pershin and Di Ventra found a way around this problem; for details, see their paper. (Hint: their strategy depends on the observation that any practical memristor has a maximum resistance, which can’t increase even when current flows the “wrong” way.)
The illustration above (reproduced courtesy of Pershin and Di Ventra) shows the path identified by a (simulated) grid of memristors for a maze that has two solutions. The red nodes, with the lowest resistance, are common to both paths; the blue and green sections differ in resistance because they differ in length.
I suppose you could also solve mazes with ordinary resistors. Just wire them up in the same way, run a healthy current from entrance to exit, and take a thermal infrared photograph.
• • •
My second postscript concerns an omission. A comment from Mark Myatt and a letter from James R. Biard both point out that I neglected to mention an important predecessor of the memristor. This was the memistor—note the ever-so-slightly different spelling—invented in 1960 by Bernard Widrow and Marcian E. Hoff at Stanford in connection with their Adaline system of neural networks. The memistor was the part of the artificial neuron that assigned a weight to each input signal. A Stanford tech report gives a detailed description.
The memistor is the only computational device I’ve ever heard about whose underlying technology is electroplating. In the prototype version, the core element was a carbon rod—specifically, a pencil lead. In its native state, this slender carbon cylinder has a resistance of about 5 ohms, but plating a thin layer of copper onto the surface reduces the resistance to about 0.5 ohm. The process is reversible and almost linear over a defined range: The conductivity is proportional to the total plating charge, which is the time integral of the plating current.
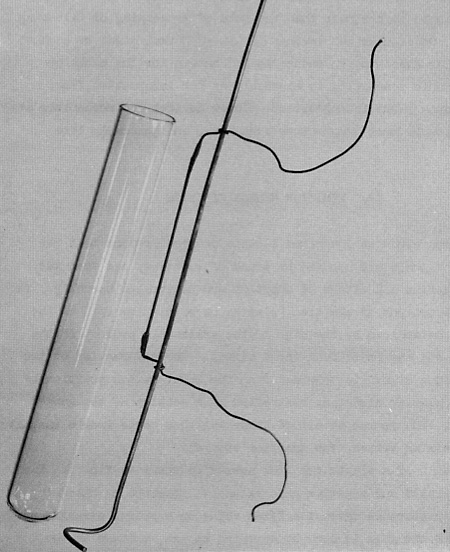
In the photo, the carbon rod is the thinner straight piece; it has insulated copper wires soldered to its ends, and those wires in turn are mounted to a heavier copper rod that both provides mechanical support and serves as the anode in the electroplating cell—the source and sink of deposited metal ions. In operation, the assembly fits inside the test tube, which is filled with a sulfuric acid–copper sulfate solution. In case you’d like to try building your own memistor, Widrow and Hoff offer some practical advice of the kind that’s all too scant in most recent computer engineering publications. They recommend a Fineline H (medium hard) pencil lead, and they suggest polishing it with steel wool. Adding a “brightener” agent to the plating bath eliminates hysteresis in the plating-deplating cycle.
The evolution of computer technology in the years after 1960 did not follow the path of electrochemistry. But it would be a big mistake to dismiss Widrow and Hoff as eccentrics off in the bushes exploring fringe ideas. At the time, Hoff was Widrow’s doctoral student. A decade later he was employee number 12 at Intel and one of the inventors of the first microprocessor.
So why didn’t I tell this wonderful story in my American Scientist article? Well, I can mumble various excuses. Only so much stuff will fit in any one article before it bursts at the seams. And the Widrow-Hoff memistor seemed marginal because it was a three-terminal device: Current through the carbon rod is controlled by a separate plating current between the copper anode and the carbon. The memristor devices invented later have only two terminals, which puts them in a different category of circuit elements. Roughly speaking, the memistor was a weird transistor, whereas the memristor is a weird resistor.
Anyway, that’s how I persuaded myself that it was okay to ignore the memistor. But the decision was a mistake, and I’m grateful to my readers for prodding me to correct it here.
Thanks for the link to the article. It’s particularly interesting that the layout of a memristor memory array mirrors that of magnetic core memory as used in the PDP-8/M on which I cut my teeth as a programmer. I well remember the rectangular grid of 49,152 little ferrite doughnuts (representing 4K of 12-bit words; the box in question had two of these), with wires running along the rows and columns and piercing each doughnut hole.
Cores, like memristors, also retained their memory after the power was off. You could literally halt the CPU, power down the system, power it up again minutes or a day later, toggle in the values of the accumulator and PC from the front panel, and push the CONT switch — and the current program would resume from where it left off.