Earlier this year Matt Welsh announced the end of programming. He wrote, in Communications of the ACM:
I believe the conventional idea of “writing a program” is headed for extinction, and indeed, for all but very specialized applications, most software, as we know it, will be replaced by AI systems that are trained rather than programmed. In situations where one needs a “simple” program (after all, not everything should require a model of hundreds of billions of parameters running on a cluster of GPUs), those programs will, themselves, be generated by an AI rather than coded by hand.
A few weeks later, in an online talk, Welsh broadened his deathwatch. It’s not only the art of programming that’s doddering toward the grave; all of computer science is “doomed.” (The image below is a screen capture from the talk.)
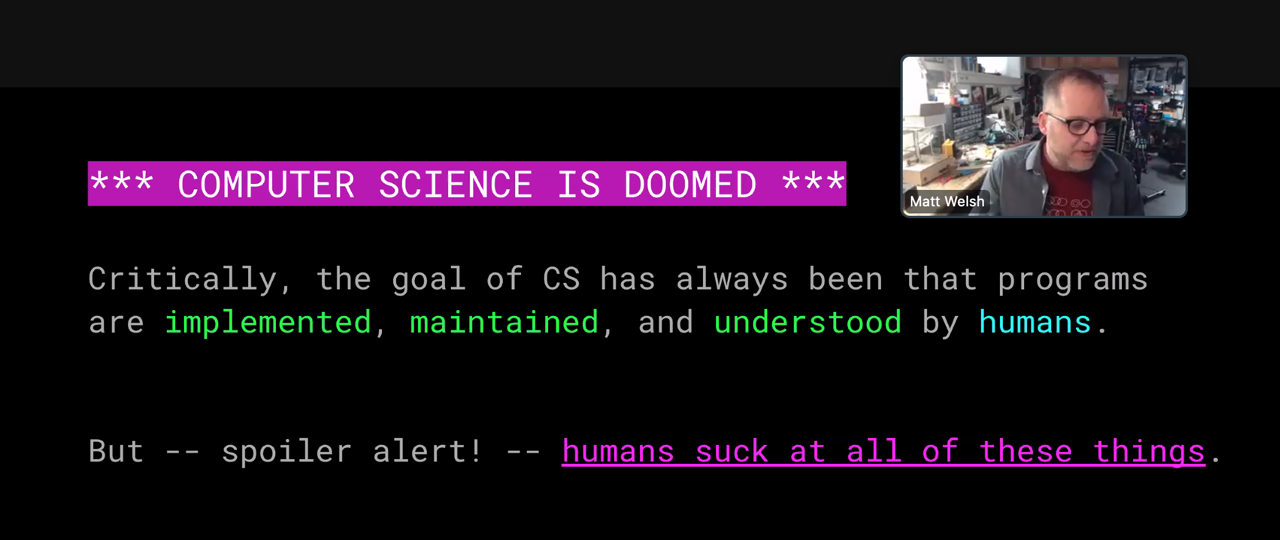
The bearer of these sad tidings does not appear to be grief-stricken over the loss. Although Welsh has made his career as a teacher and practitioner of computer science (at Harvard, Google, Apple, and elsewhere), he seems eager to move on to the next thing. “Writing code sucks anyway!” he declares.
My own reaction to the prospect of a post-programming future is not so cheery. In the first place, I’m skeptical. I don’t believe we have yet crossed the threshold where machines learn to solve interesting computational problems on their own. I don’t believe we’re even close to that point, or necessarily heading in the right direction. Furthermore, if it turns out I’m wrong about all this, my impulse is not to acquiesce but to resist. I, for one, do not welcome our new AI overlords. Even if they prove to be better programmers than I am, I’ll hang onto my code editor and compiler all the same, thank you. Programming sucks? For me it has long been a source of pleasure and enlightenment. I find it is also a valuable tool for making sense of the world. I’m never sure I understand an idea until I can reduce it to code. To get the benefit of that learning experience, I have to actually write the program, not just say some magic words and summon a genie from Aladdin’s AI lamp.
Large Language Models
The idea that a programmable machine might write its own programs has deep roots in the history of computing. Charles Babbage hinted at the possibility as early as 1836, in discussing plans for his Analytical Engine. When Fortran was introduced in 1957, it was officially styled “The FORTRAN Automatic Coding System.” Its stated goal was to allow a computer “to code problems for itself and produce as good programs as human coders (but without the errors).”
Fortran did not abolish the craft of programming (or the errors), but it made the process less tedious. Later languages and other tools brought further improvements. And the dream of fully automatic programming has never died. Machines seem better suited to programming than most people are. Computers are methodical, rule-bound, finicky, and literal-minded—all traits that we associate (rightly or wrongly) with ace programmers.
Ironically, though, the AI systems now poised to take on programming chores are strangely uncomputerlike. Their personality is more Deanna Troi than Commander Data. Logical consistency, cause-and-effect reasoning, and careful attention to detail are not among their strengths. They have moments of uncanny brilliance, when they seem to be thinking deep thoughts, but they are also capable of spectacular failures—blatant and brazen lapses of rationality. They bring to mind the old quip: To err is human, to really foul things up requires a computer.
The latest cohort of AI systems are known as large language models (LLMs). Like most other recent AI inventions, they are built atop an artificial neural network, a multilayer structure inspired by the architecture of the brain. The nodes of the network are analogous to biological neurons, and the connections between nodes play the role of synapses, the junctions where signals pass from one neuron to another. Training the network adjusts the strength, or weight, of the connections. In a language model, the training is done by force-feeding the network huge volumes of text. When the process is complete, the connection weights encode detailed statistics on linguistic features of the training text. In the largest models the number of weights is 100 billion or more.
The term model in this context can be misleading. The word is not used in the sense of a scale model, or miniature, like a model airplane. It refers instead to a predictive model, like the mathematical models common in the sciences. Just as a model of the atmosphere predicts tomorrow’s weather, a language model predicts the next word in a sentence.
The best known LLM is ChatGPT, which was released to the public last fall, to great fanfare. The initials GPT
ChatGPT elicits both admiration and alarm for its way with words, its gift of gab, its easy fluency in English and other languages. The chatbot can imitate famous authors, tell jokes, compose love letters, translate poetry, write junk mail, “help” students with their homework assignments, and fabricate misinformation for political mischief. For better or worse, these linguistic abilities represent a startling technical advance. Computers that once struggled to frame a single intelligible sentence have suddenly become glib wordsmiths. What GPT says may or may not be true, but it’s almost always well-phrased.
Soon after ChatGPT was announced, I was surprised to learn that its linguistic mastery extends to programming languages. It seems the training set for the model included not just multiple natural languages but also quantities of program source code from public repositories such as GitHub. Based on this resource, GPT was able to write new programs on command. I found this surprising because computers are so fussy and unforgiving about their inputs. A human raeder will strive to make sense of an utterance despite small errors such as misspellings, but a computer will barf if it’s given a program with even one stray comma or mismatched parenthesis. A language model, with its underlying statistical or probabilistic nature, seemed unlikely to sustain the required precision for more than a few lines.
I was wrong about this. A key innovation in the new LLMs, known as the attention mechanism, addresses this very issue. When I began my own experiments with ChatGPT, I soon found that it can indeed produce programs free of careless syntax errors.
But other problems cropped up.
Climbing the word ladder
When you sit down to chat with a machine, you immediately face the awkward question: “What shall we talk about?” I was looking for a subject that would serve as a fair measure of ChatGPT’s programming prowess. I wanted a problem that can be solved by computational means, but that doesn’t call for doing much arithmetic, which is known to be one of the weak points of LLMs. I settled on a word puzzle invented 150 years ago by Lewis Carroll and analyzed in depth by Donald E. Knuth in the 1990s.
In the transcript below, my side of each exchange is labeled BR; the rosette , which is an OpenAI logo, designates ChatGPT’s responses.
As I watched these sentences unfurl on the screen—the chatbot types them out letter by letter, somewhat erratically, as if pausing to gather its thoughts—I was immediately struck by the system’s facility with the English language. In plain, sturdy prose, GPT catalogs all the essential features of a word ladder: It’s a game or puzzle, you proceed from word to word by changing one letter at a time, each rung of the ladder must be an English word, the aim is to find the shortest possible sequence from the starting word to the target word. I couldn’t explain it better myself. Most helpful of all is the worked example of COLD -> WARM.
It’s not just the individual sentences that give an impression of linguistic competence. The sentences are organized in paragraphs, and the paragraphs are strung together to form a coherent discourse. Bravo!
Also remarkable is the bot’s ability to handle vague and slapdash inputs. My initial query was phrased as a yes-or-no question, but ChatGPT correctly interpreted it as a request: “Tell me what you know about word ladders.” My second instruction neglects to include any typographic hints showing that lead and gold are to be understood as words, not metals. The chatbot would have been within its rights to offer me an alchemical recipe, but instead it supplied the missing quotation marks.
Setting aside all this linguistic and rhetorical sophistication, however, what I really wanted to test was the program’s ability to solve word-ladder problems. The two examples in the transcript above can both be found on the web, and so they might well have appeared in ChatGPT’s training data. In other words, the LLM may have memorized the solutions rather than constructed them. So I submitted a tougher assignment:
At first glance, it seems ChatGPT has triumphed again, solving an instance of the puzzle that I’m pretty sure it has not seen previously. But look closer. MARSH -> MARIS requires two letter substitutions, and so does PARIL -> APRIL. The status of MARIS and PARIL as “valid words” might also be questioned. I lodged a complaint:
Whoa! The bot offers unctuous confessions and apologies, but the “corrected” word ladder is crazier than ever. It looks like we’re playing Scrabble with Humpty Dumpty, who declares “APRCHI is a word if I say it is!” and then scatters all the tiles.
This is not an isolated, one-of-a-kind failure. All of my attempts to solve word ladders with ChatGPT have gone off the rails, although not always in the same way. In one case I asked for a ladder from REACH to GRASP. The AI savant proposed this solution:
REACH -> TEACH -> PEACH -> PEACE -> PACES -> PARES -> PARSE ->
PARSE -> PARSE -> PARSE -> PARKS -> PARKS -> PARKS -> PARKS ->
PARES -> GRASP.
And there was this one:
SWORD -> SWARD -> REWARD -> REDRAW -> REDREW ->
REDREW -> REDREW -> REDREW -> REDRAW -> REPAID ->
REPAIR -> PEACE
Now we are babbling like a young child just learning to count: “One, two, three, four, three, four, four, four, seven, blue, ten!”
All of the results I have shown so far were recorded with version 3.5 of ChatGPT. I also tried the new-and-improved version 4.0, which was introduced in March. The updated bot exudes the same genial self-assurance, but I’m afraid it also has the same tendency to drift away into oblivious incoherence:
The ladder starts out well, with four steps that follow all the rules. But then the AI mind wanders. From PLAGE to PAGES requires four letter substitutions. Then comes PASES, which is not a word (as far as I know), and in any case is not needed here, since the sequence could go directly from PAGES to PARES. More goofiness ensues. Still, I do appreciate the informative note about PLAGE.
Recently I’ve also had a chance to try out Llama 2, an LLM published by Meta (the Facebook people). Although this model was developed independently of GPT, it seems to share some of the same mental quirks, such as laying down rules and then blithely ignoring them. When I asked for a ladder connecting REACH to GRASP, this is what Llama 2 proposed:
REACH -> TEACH -> DEACH -> LEACH -> SPEECH -> SEAT ->
FEET -> GRASP
What can I say? I guess a bot’s REACH should exceed its GRASP.
Oracles and code monkeys
Matt Welsh mentions two modes of operation for a computing system built atop a large language model. So far we’ve been working in what I’ll call oracle mode, where you ask a question and the computer returns an answer. You supply a pair of words, and the system finds a ladder connecting them, doing whatever computing is needed to get there. You deliver a shoebox full of financial records, and the computer fills out your Form 1040. You compile historical climate data, and the computer predicts the global average temperature in 2050.
The alternative to an AI oracle is an AI code monkey. In this second mode, the machine does not directly answer your question or perform your calculation; instead it creates a program that you can then run on a conventional computer. What you get back from the bot is not a word ladder but a program to generate word ladders, written in the programming language of your choice. Instead of a completed tax return you get tax-preparation software; instead of a temperature prediction, a climate model.
Let’s give it a try with ChatGPT 3.5:
Again, a cursory glance at the output suggests a successful performance. ChatGPT seems to be just as fluent in JavaScript as it is in English. It knows the syntax for if, while, and for statements, as well as all the finicky punctuation and bracketing rules. The machine-generated program appears to bring all these components together to accomplish the specified task. Also note the generous sprinkling of explanatory comments, which are surely meant for our benefit, not for its. Likewise the descriptive variable names (currentWord, newWord, ladder).
ChatGPT has also, on its own initiative, included instructions for running the program on a specific example (MARCH to APRIL), and it has printed out a result, which matches the answer it gave in our earlier exchange. Was that output generated by actually running the program? ChatGPT does not say so explicitly, but it does make the claim that if you run the program as instructed, you will get the result shown (in all its nonsensical glory).
We can test this claim by loading the program into a web browser or some other JavaScript execution environment. The verdict: Busted! The program does run, but it doesn’t yield the stated result. The program’s true output is: MARCH -> AARCH -> APRCH -> APRIH -> APRIL. This sequence is a little less bizarre, in that it abides by the rule of changing only one letter at a time, and all the “words” have exactly five letters. On the other hand, none of the intermediate “words” are to be found in an English dictionary.
There’s an easy algorithm for generating the sequence MARCH -> AARCH -> APRCH -> APRIH -> APRIL. Just step through the start word from left to right, changing the letter at each position so that it matches the corresponding letter in the goal word. Following this rule, any pair of five-letter words can be laddered in no more than five steps. MARCH -> APRIL takes only four steps because the R in the middle doesn’t need to be changed. I can’t imagine an easier way to make word ladders—assuming, of course, that you’re willing to let any and every mishmash of letters count as a word.
The program created by ChatGPT could use this quick-and-dirty routine, but instead it does something far more tedious: It constructs all possible ladders whose first rung is the start word, and continues extending those ladders until it stumbles on one that includes the target word. This is a brute-force algorithm of breathtaking wastefulness. Each letter of the start word can be altered in 25 ways. Thus a five-letter word has 125 possible successors. By the time you get to a five-rung ladder, there are 190 million possibilities. (The examples I have presented here, such as MARCH -> APRIL and REACH -> GRASP, have one unchanging letter, and so the solutions require only four steps. Trying to compute full five-step solutions exhausted my patience.)
Version 4 as code monkey
Let’s try the same code-writing exercise with ChatGPT 4. Given the identical prompt, here’s how the new bot responded:
The program has the same overall structure (a while loop with two nested for loops inside), and it adopts the same algorithmic strategy (generating all strings that differ from a given word at exactly one position). But there’s a big novelty in the GPT-4 version: acknowledgment that a word list is essential. And with this change we finally have some hope of generating a ladder made up of genuine words.
Although GPT-4 recognizes the need for a list, it supplies only a placeholder, namely the 10-word sequence it confected for the REACH -> GRASP example given above. This stub of a word list isn’t good for much—not even for regenerating the bogus REACH-to-GRASP ladder. If you try to do that, the program will report that no ladder exists. This outcome is not incorrect, since the 10 given words do not form a valid pathway that changes just one letter on each step.
Even if the words in the list were well-chosen, a vocabulary of size 10 is awfully puny. Producing a bigger list of words seems like a task that would be easy for a language model. After all, the LLM was trained on a vast corpus of text, in which nearly all English words are likely to appear at least once, and common words would turn up millions of times. Can’t the bot just extract a representative sample of those words? The answer, apparently, is no. Although GPT might be said to have “read” all that text, it has not stored the words in any readily accessible form. (The same is true of a human reader. Can you, by thinking back over a lifetime of reading, list the 10 most common five-letter words in your vocabulary?)
When I asked ChatGPT 4 to produce a word list, it demurred apologetically: “I’m sorry for the confusion, but as an AI developed by OpenAI, I don’t have direct access to a database of words or the ability to fetch data from external sources….” So I tried a bit of trickery, asking the bot to write a 1,000-word story and then sort the story’s words in order of frequency. This ruse worked, but the sample was too small to be of much use. With persistence, I could probably coax an acceptable list from GPT, but instead I took a shortcut. After all, I am not an AI developed by OpenAI, and I have access to external resources. I appropriated the list of 5,757 five-letter English words that Knuth compiled for his experiments with word ladders. Equipped with this list, the program written by GPT-4 finds the following nine-step ladder:
REACH -> PEACH -> PEACE -> PLACE -> PLANE ->
PLANS -> GLANS -> GLASS -> GRASS -> GRASP
This result exactly matches the output of Knuth’s own word-ladder program, which he published 30 years ago in The Stanford Graphbase.
At this point I must concede that ChatGPT, with a little outside help, has finally done what I asked of it. It has written a program that can construct a valid word ladder. But I still have reservations. Although the programs written by GPT-4 and by Knuth produce the same output, the programs themselves are not equivalent, or even similar.
Knuth approaches the problem from the opposite direction, starting not with the set of all possible five-letter strings—there are not quite 12 million of them—but with his much smaller list of 5,757 common English words. He then constructs a graph (or network) in which each word is a node, and two nodes are connected by an edge if and only if the corresponding words differ by a single letter. The diagram below shows a fragment of such a graph.
A fragment of a graph links 16 words according to the word-ladder rule: If one word can be converted into another word by changing a single letter, then those two words are connected by an edge in the graph. A word ladder is a path along the edges of the graph, such as leash -> leach -> reach -> retch. Donald E. Knuth’s graph for five-letter words has 5,757 nodes and 14,135 edges. The largest connected component of the graph includes 4,493 words.
In the graph, a word ladder is a sequence of edges leading from a start node to a goal node. The optimal ladder is the shortest such path, traversing the smallest number of edges. For example, the optimal path from leash to retch is leash -> leach -> reach -> retch, but there are also longer paths, such as leash -> leach -> beach -> peach -> reach -> retch. For finding shortest paths, Knuth adopts an algorithm devised in the 1950s by Edsger W. Dijkstra.
Knuth’s word-ladder program requires an up-front investment to convert a simple list of words into a graph. On the other hand, it avoids the wasteful generation of thousands or millions of five-letter strings that cannot possibly be elements of a word latter. In the course of solving the REACH -> GRASP problem, the GPT-4 program produces 219,180 such strings; only 2,792 of them (a little more than 1 percent) are real words.
If the various word-ladder programs I’ve been describing were student submissions, I would give a failing grade to the versions that have no word list. The GPT-4 program with a list would pass, but I’d give top marks only to the Knuth program, on grounds of both efficiency and elegance.
Why do the chatbots favor the inferior algorithm? You can get a clue just by googling “word-ladder program.” Almost all the results at the top of the list come from websites such as Leetcode, GeeksForGeeks and RosettaCode. These sites, which apparently cater to job applicants and competitors in programming contests, feature solutions that call for generating all 125 single-letter variants of each word, as in the GPT programs. Because sites like these are numerous—there seem to be hundreds of them—they outweigh other sources, such as Knuth’s book (if, indeed, such texts even appear in the training set). Does that mean we should blame the poor choice of algorithm not on GPT but on Leetcode? I would point instead to the unavoidable weakness of a protocol in which the most frequent answer is, by default, the right answer.
A further, related concern nags at me whenever I think about a world in which LLMs are writing all our software. Where will new algorithms come from? An LLM might get creative in remixing elements of existing programs, but I don’t see any way it would invent something wholly new and better.
Enough with the word ladders already!
I admit I’ve gone overboard, torturing ChatGPT with too many variations of one peculiar (and inconsequential) problem. Maybe the LLMs would perform better on other computational tasks. I have tried several, with mixed results. I want to discuss just one of them, where I find ChatGPT’s efforts rather poignant.
Working with ChatGPT 3.5, I ask for the value of the 100th Fibonacci number. Note that my question is phrased in oracle mode; I ask for the number, not for a program to calculate it. Nevertheless, ChatGPT volunteers to write a Fibonacci program, and then presents what purports to be the program’s output.
The algorithm implemented by this program is mathematically correct; it follows directly from the definition of a Fibonacci number as a member of the sequence beginning {0, 1}, with every subsequent element equal to the sum of the previous two terms. The answer given is also correct: 354224848179261915075 is indeed the 100th Fibonacci number. So what’s the problem? It’s the middle statement: “When you run this code, it will output the 100th Fibonacci number.” That’s not true. If you run the code, what you’ll get back is the incorrect value 354224848179262000000. BigInt data type that solves this problem, but BigInts must be specified explicitly, and the ChatGPT program does not do so.
Giving the same task to ChatGPT 4.0 takes us on an even stranger journey. In the following interaction I had activated Code Interpreter, a ChatGPT plugin that allows the system to test and run some of the code it writes. Apparently making use of this facility, the bot first proposes a program that fails for unknown reasons:
Here ChatGPT is writing in Python, which is the main programming language supported by Code Interpreter. The first attempt at writing a program is based on exponentiation of the Fibonacci matrix:
$$\mathrm{F}_1=\left[\begin{array}{ll}
1 & 1 \\
1 & 0
\end{array}\right].$$
This is a well-known and efficient method, and the program implements it correctly. For mysterious reasons, however, Code Interpreter fails to execute the program. (The code runs just fine in a standard Python environment, and returns correct answers.)
At this point the bot pivots and takes off in a wholly new direction, proposing to calculate the desired Fibonacci value via the mathematical identity known as Binet’s formula. It gets as far as writing out the mathematical expression, but then has another change of mind. It correctly foresees problems with numerical precision: The formula would yield an exact result if it were given an exact value for the square root of 5, but that’s not feasible.
And so now ChatGPT takes yet another tack, resorting to the same iterative algorithm used by version 3.5. This time we get a correct answer, because Python (unlike JavaScript) has no trouble coping with large integers.
I’m impressed by this performance, not just by the correct answer but also by the system’s courageous perseverance. ChatGPT soldiers on even as it flails about, puzzled by unexpected difficulties but refusing to give up. “Hmm, that matrix method should have worked. But, no matter, we’ll try Binet’s formula instead… Oh, wait, I forgot… Anyway, there’s no need to be so fancy-pants about this. Let’s just do it the obvious, plodding way.” This strikes me as a very human approach to problem-solving. It’s weird to see such behavior in a machine.
Scoring successes and failures
My little experiments have left me skeptical of claims that AI oracles and AI code monkeys are about to elbow aside human programmers. I’ve seen some successes, but more failures. And this dismal record was compiled on relatively simple computational tasks for which solutions are well known and widely published.
Others have conducted much broader and deeper evaluations of LLM code generation. In the bibliography at the end of this article I’ve listed five such studies. I’d like to briefly summarize a few of the results they report.
Two years ago, Mark Chen and a roster of 50+ colleagues at OpenAI devoted much effort to measuring the accuracy of Codex, an offshoot of ChatGPT 3 specialized for writing program code. (Codex has since become the engine driving GitHub Copilot, a “programmer’s assistant.”) Chen et al. created a suite of 164 tasks to be accomplished by writing Python programs. The tasks were mainly of the sort found in textbook exercises, programming contests, and the (strangely voluminous) literature on how to ace an interview for a coding job. Most of the tasks can be accomplished with just a few lines of code. Examples: Count the vowels in a given word, determine whether an integer is prime or composite.
The Chen group also gave some thought to defining criteria of success and failure. Because the LLM process is nondeterministic—word choices are based on probabilities—the model might generate a defective program on the first try but eventually come up with a correct response if it’s allowed to keep trying. A parameter called temperature controls the amount of nondeterminism. At zero temperature the model invariably chooses the most probable word at every step; as the temperature rises, randomness is introduced, allowing less probable words to be selected. Chen et al. took account of this potential for variation by adopting three benchmarks of success:
| pass@1: | the LLM generates a correct program on the first try |
| pass@10: | at least one of 10 generated programs is correct |
| pass@100: | at least one of 100 generated programs is correct |
Pass@1 tests were conducted at zero temperature, so that the model would always give its best-guess result. The pass@10 and pass@100 trials were done at higher temperatures, allowing the system to explore a wider variety of potential solutions.
The authors evaluated several versions of Codex on all 164 tasks. For the largest and most capable version of Codex, the pass@1 rate was about 29 percent, the pass@10 rate 47 percent, and pass@100 reached 72 percent. Looking at these numbers, should we be impressed or appalled? Is it cause for celebration that Codex gets it right on the first try almost a third of the time (when the temperature is set to zero)? Or that the success ratio climbs to almost three-fourths if you’re willing to sift through 100 proposed programs looking for one that’s correct? My personal view is this: If you view the current generation of LLMs as pioneering efforts in a long-term research program, then the results are encouraging. But if you consider this technology as an immediate replacement for hand-coded software, it’s quite hopeless. We’re nowhere near the necessary level of reliability.
Other studies have yielded broadly similar results. Federico Cassano et al. assess the performance of several LLMs generating code in a variety of programming languages; they report a wide range of pass@1 rates, but only two exceed 50 percent. Alessio Buscemi tested ChatGPT 3.5 on 40 coding tasks, asking for programs written in 10 languages, and repeating each query 10 times. Of the 4,000 trials, 1,833 resulted in code that could be compiled and executed. Zhijie Liu et al. based their evaluation of ChatGPT on problems published on the Leetcode website. The results were judged by submitting the generated code to the automated Leetcode grading process. The acceptance rate, averaged across all problems, ranged from 31 percent for programs written in C to 50 percent for Python programs. Liu et al. make another interesting observation: ChatGPT scores much worse on problems published after September 2021, which was the cutoff date for the GPT training set. They conjecture that the bot may do better with the earlier problems because it already saw the solutions during training.
A very recent paper by Li Zhong and Zilong Wang goes beyond the basic question of program correctness to consider robustness and reliability. Can the generated program respond appropriately to malformed input or to external errors, as when trying to open a file that doesn’t exist? Even when the prompt to the LLM included an example showing how to handle such issues correctly, Zhong and Wang found that the generated code failed to do so in 30 to 50 percent of cases.
Beyond these discouraging results, I have further misgivings of my own. Almost all the tests were conducted with short code snippets. An LLM that stumbles when writing a 10-line program is likely to have much greater difficulty with 100 lines or 1,000. Also, simple pass/fail grading is a very crude measure of code quality. Consider the primality test that was part of the Chen group’s benchmarking suite. Here is one of the Codex-written programs:
def is_prime(n):
prime = True
if n==1:
return False
for i in range(2, n):
if n % i == 0:
prime = False
return prime
This code is scored as correct—as it should be, since it will never misclassify a prime as composite, or vice versa. However, you may not have the patience—or the lifespan—to wait for a verdict when \(n\) is large. The algorithm attempts to divide \(n\) by every integer from 2 to \(n-1\).
The unreasonable effectiveness of LLMs
It’s still early days for large language models. ChatGPT was published less than a year ago; the underlying technology is only about six years old. Although I feel pretty sure of myself declaring that LLMs are not yet ready to conquer the world of coding, I can’t be quite so confident predicting that they never will be. The models will surely improve, and we’ll get better at using them. Already there is a budding industry offering guidance on “prompt engineering” as a way to get the most out of every query.
Another way to bolster the performance of an LLM might be to form a hybrid with another computational system, one equipped with tools for logic and reasoning rather than purely verbal analysis. Doug Lenat, just before his recent death, proposed combining an LLM with Cyc, a huge database of common knowledge that he had labored to build over four decades. And Stephen Wolfram is working to integrate ChatGPT into Wolfram|Alpha, an online collection of curated data and algorithms.
Still, some of the obstacles that trip up LLM program generators look difficult to overcome.
Language models work their magic through simple means: In the course of composing a sentence or a paragraph, the LLM chooses its next word based on the words that have come before. It’s like writing a text message on your phone: You type “I’ll see you…” and the software suggests a few alternative continuations: “tomorrow,” “soon,” “later.” In the LLM each candidate is assigned a probability, calculated from an analysis of all the text in the model’s training set.
The idea of text generation through this kind of statistical analysis was first explored more than a century ago by the Russian mathematician A. A. Markov. His procedure is now known as an n-gram model, where n is the number of words (or characters, or other symbols) to be considered in choosing the next element of the sequence. I have long been fascinated by the n-gram process, though mostly for its comedic possibilities. (In an essay published 40 years ago, I referred to it as “the fine art of turning literature into drivel.”)
Of course ChatGPT and the other recent LLMs are not merely n-gram models. Their neural networks capture statistical features of language that go well beyond a sequence of n contiguous symbols. Of particular importance is the attention mechanism, which is capable of tracking dependencies between selected symbols at arbitrary distances. In natural languages this device is useful for maintaining agreement of subject and verb, or for associating a pronoun with its referent. In a programming language, the attention mechanism ensures the integrity of multipart syntactic constructs such as if... then... else, and it keeps brackets properly paired and nested.
ChatGPT and other LLMs also benefit from reinforcement learning supervised by human readers. When a reader rates the quality and accuracy of the model’s output, the positive or negative feedback helps shape future responses.
Even with these refinements, however, an LLM remains, at bottom, a device for constructing a new text based on probabilities of word occurrence in existing texts. To my way of thinking, that’s not thinking. It’s something shallower, focused on words rather than ideas. Given this crude mechanism, I am both amazed and perplexed at how much the LLMs can accomplish.
For decades, architects of AI believed that true intelligence (whether natural or artificial) requires a mental model of the world. To make sense of what’s going on around you (and inside you), you need intuition about how things work, how they fit together, what happens next, cause and effect. Lenat insisted that the most important kinds of knowledge are those you acquire long before you start reading books. You learn about gravity by falling down. You learn about entropy when you find that a tower of blocks is easy to knock over but harder to rebuild. You learn about pain and fear and hunger and love—all this in infancy, before language begins to take root. Experiences of this kind are unavailable to a brain in a box, with no direct access to the physical or the social universe.
LLMs appear to be the refutation of these ideas. After all, they are models of language, not models of the world. They have no embodiment, no physical presence that would allow them to learn via the school of hard knocks. Ignorant of everything but mere words, how do they manage to sound so smart, so worldly?
On this point opinions differ. Critics of the technology say it’s all fakery and illusion. A celebrated (or notorious?) paper by Emily Bender, Timnit Gebru, and others dubs the models “stochastic parrots.” Although an LLM may speak clearly and fluently, the critics say, it has no idea what it’s talking about. Unlike a child, who learns mappings between words and things—Look! a cow, a cat, a car—the LLM can only associate words with other words. During the training process it observes that umbrella often appears in the same context as rain, but it has no experience of getting wet. The model’s modus operandi is akin to the formalist approach in mathematics, where you push symbols around on the page, moving them from one side of the equation to the other, without ever asking what the symbols symbolize. To paraphrase Saul Gorn: A formalist can’t understand a theory unless it’s meaningless.

Proponents of LLMs see it differently. One of their stronger arguments is that language models learn syntax, or grammar,
Ilya Sutskever, the chief scientist at OpenAI, made this point forcefully in a conversation with Jensen Huang of Nvidia:
When we train a large neural network to accurately predict the next word, in lots of different texts from the internet, what we are doing is that we are learning a world model… It may look on the surface that we are just learning statistical correlations in text, but it turns out that to just learn the statistical correlations in text, to compress them really well, what the neural network learns is some representation of the process that produced the text. This text is actually a projection of the world. There is a world out there, and it has a projection on this text. And so what the neural network is learning is more and more aspects of the world, of people, of the human conditions, their hopes, dreams and motivations, their interactions and situations that we are in, and the neural network learns a compressed, abstract, usable representation of that.
Am I going to tell you which of these contrasting theories of LLM mentality is correct? I am not. Neither alternative appeals to me. If Bender et al. are right, then we must face the fact that a gadget with no capacity to reason or feel, no experience of the material universe or social interactions, no sense of self, can do a passable job of writing college essays, composing rap songs, and giving advice to the lovelorn. Knowledge and logic and emotion count for nothing; glibness is all. It’s a subversive proposition. If ChatGPT can fool us with this mindless showmanship, perhaps we too are impostors whose sound and fury signifies nothing.
On the other hand, if Sutskever is right, then much of what we prize as the human experience—the sense of personhood that slowly evolves as we grow up and make our way through life—can be acquired just by reading gobs of text scraped from the internet. If that’s true, then I didn’t actually have to endure the unspeakable agony that is junior high school; I didn’t have to make all those idiotic blunders that caused such heartache and hardship; there was no need to bruise my ego bumping up against the world. I could have just read about all those things, in the comfort of my armchair; mere words would have brought me to a state of clear-eyed maturity without all the stumbling and suffering through the vale of soul-making.
Both the critics and the defenders of LLMs tend to focus on natural-language communication between the machine and a human conversational partner—the chatty part of ChatGPT. In trying to figure out what’s happening inside the neural network, it might be helpful to pay more attention to the LLM in the role of programmer, where both parties to the conversation are computers. I can offer three arguments in support of this suggestion. First, people are too easy to fool. We make allowances, fill in blanks, silently correct mistakes, supply missing context, and generally bend over backwards to make sense of an utterance, even when it makes no sense. Computers, in contrast, are stern judges, with no tolerance for bullshit.
Second, if we are searching for evidence of a mental model inside the machine, it’s worth noting that a model of a digital computer ought to be simpler than a model of the whole universe. Because a computer is an artifact we design and build to our our own specifications, there’s not much controversy about how it works. Mental models of the universe, in contrast, are all over the map. Some of them begin with a big bang followed by cosmic inflation; some are ruled by deities and demons; some feature an epic battle between east and west, Jedi and Sith, red and blue, us and them. Which of these models should we expect to find imprinted on the great matrix of weights inside GPT? They could all be there, mixed up willy-nilly.
Third, programming languages have an unusual linguistic property that binds them tightly to actions inside the computer. The British philosopher J. L. Austin called attention to a special class of words he designated performatives. These are words that don’t just declare or describe or request; they actually do something when uttered. Austin’s canonical example is the statement “I do,” which, when spoken in the right context, changes your marital status. In natural language, performative words are very rare, but in computer programs they are the norm. Writing x = x + 1, in the right context, actually causes the value of x to be incremented. That direct connection between words and actions might be helpful when you’re testing whether a conceptual model matches reality.
I remain of two minds (or maybe more than two!) about the status and the implications of large language models for computer science. The AI enthusiasts could be right. The models may take over programming, along with many other kinds of working and learning. Or they may fizzle, as other promising AI innovations have done. I don’t think we’ll have too long to wait before answers begin to emerge.
Further Reading
Transformers and Large Language Models
Vaswani, Ashish, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, ?ukasz Kaiser, and Illia Polosukhin. Attention is all you need. In 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA. https://arxiv.org/abs/1706.03762.
Amatriain, Xavier. 2023. Transformer models: an introduction and catalog. https://arxiv.org/abs/2302.07730.
Goldberg,Yoav. 2015. A Primer on neural network models for natural language processing. https://arxiv.org/abs/1510.00726.
Word ladders
Carroll, Lewis. 1879. Doublets: A Word-Puzzle. London: Macmillan and Co. (Available online at Google Books.)
Dewdney, A. K. 1987. Computer Recreations: Word ladders and a tower of Babel lead to computational heights defying assault. Scientific American 257(2):108–111.
Gardner, Martin. 1994. Word Ladders: Lewis Carroll’s Doublets. Math Horizons, November, 1994, pp. 18–19.
Knox, John. 1927. Word-Change Puzzles. Chicago: Laird and Lee. (Available online at archive.org.)
Knuth, Donald E. 1993. The Stanford Graphbase: A Platform for Combinatorial Computing. New York: ACM Press (Addison-Wesley Publishing).
Nabokov, Vladimir. 1962. Pale Fire. New York: G. P. Putnam’s Sons. [See the index under "word golf."]
LLMs for Programming
Dowdell, Thomas, and Hongyu Zhang. 2020. Language modelling for source code with Transformer-XL. https://arxiv.org/abs/2007.15813.
Karpathy, Andrej. 2017. Software 2.0 Medium.
Zhang, Shun, Zhenfang Chen, Yikang Shen, Mingyu Ding, Joshua B. Tenenbaum, and Chuang Gan. 2023. Planning with large language models for code generation. https://arxiv.org/abs/2303.05510.
Evaluations of LLMs as program generators
Buscemi, Alessio. 2023. A comparative study of code generation using ChatGPT 3.5 across 10 programming languages. https://arxiv.org/abs/2308.04477.
Cassano, Federico, John Gouwar, Daniel Nguyen, Sydney Nguyen, Luna Phipps-Costin, Donald Pinckney, Ming-Ho Yee, Yangtian Zi, Carolyn Jane Anderson, Molly Q Feldman, Arjun Guha, Michael Greenberg, Abhinav Jangda. 2022. MultiPL-E: A scalable and extensible approach to benchmarking neural code generation. https://arxiv.org/abs/2208.08227
Chen, Mark, Jerry Tworek, Heewoo Jun, Qiming Yuan, Henrique Ponde de Oliveira Pinto, Jared Kaplan, Harri Edwards, Yuri Burda, Nicholas Joseph, Greg Brockman, Alex Ray, Raul Puri, Gretchen Krueger, Michael Petrov, Heidy Khlaaf, Girish Sastry, Pamela Mishkin, Brooke Chan, Scott Gray, Nick Ryder, Mikhail Pavlov, Alethea Power, Lukasz Kaiser, Mohammad Bavarian, Clemens Winter, Philippe Tillet, Felipe Petroski Such, Dave Cummings, Matthias Plappert, Fotios Chantzis, Elizabeth Barnes, Ariel Herbert-Voss, William Hebgen Guss, Alex Nichol, Alex Paino, Nikolas Tezak, Jie Tang, Igor Babuschkin, Suchir Balaji, Shantanu Jain, William Saunders, Christopher Hesse, Andrew N. Carr, Jan Leike, Josh Achiam, Vedant Misra, Evan Morikawa, Alec Radford, Matthew Knight, Miles Brundage, Mira Murati, Katie Mayer, Peter Welinder, Bob McGrew, Dario Amodei, Sam McCandlish, Ilya Sutskever, Wojciech Zaremba. 2021. Evaluating large language models trained on code. https://arxiv.org/abs/2107.03374.
Liu, Zhijie, Yutian Tang, Xiapu Luo, Yuming Zhou, and Liang Feng Zhang. 2023. No need to lift a finger anymore? Assessing the quality of code generation by ChatGPT. https://arxiv.org/abs/2308.04838.
Zhong, Li, and Zilong Wang. 2023. A study on robustness and reliability of large language model code generation. https://arxiv.org/abs/2308.10335.
Do They Know and Think?
Bubeck, Sébastien, Varun Chandrasekaran, Ronen Eldan, Johannes Gehrke, Eric Horvitz, Ece Kamar, Peter Lee, Yin Tat Lee, Yuanzhi Li, Scott Lundberg, Harsha Nori, Hamid Palangi, Marco Tulio Ribeiro, and Yi Zhang. 2023. Sparks of artificial general intelligence: early experiments with GPT-4. https://arxiv.org/abs/2303.12712.
Bayless, Jacob. 2023. It’s not just statistics: GPT does reason. https://jbconsulting.substack.com/p/its-not-just-statistics-gpt-4-does
Arkoudas, Konstantine. 2023. GPT-4 can’t reason. https://arxiv.org/abs/2308.03762.
Yiu, Eunice, Eliza Kosoy, and Alison Gopnik. 2023. Imitation versus innovation: What children can do that large language and language-and-vision models cannot (yet)? https://arxiv.org/abs/2305.07666.
Piantadosi, Steven T., and Felix Hill. 2022. Meaning without reference in large language models. https://arxiv.org/abs/2208.02957.
From word models to world models: Translating from natural language to the probabilistic language of thought. 2023. Wong, Lionel, Gabriel Grand, Alexander K. Lew, Noah D. Goodman, Vikash K. Mansinghka, Jacob Andreas, and Joshua B. Tenenbaum. https://arxiv.org/abs/2306.12672.
Other Topics
Lenat, Doug. 2008. The voice of the turtle: Whatever happened to AI? AI Magazine 29(2):11–22.
Lenat, Doug, and Gary Marcus. 2023. Getting from generative AI to trustworthy AI: What LLMs might learn from Cyc. https://arxiv.org/abs/2308.04445
Wolfram, Stephen. 2023. Wolfram|Alpha as the way to bring computational knowledge superpowers to ChatGPT. Stephen Wolfram Writings. See also Introducing chat notebooks: Integrating LLMs into the notebook paradigm.
Austin, J. L. 1962. How to Do Things with Words. Second edition, 1975. Edited by J. O. Urmson and Marina Sbisà. Cambridge, MA: Harvard University Press.