Here in New Orleans there’s nothing to make a snowball out of—not even a semisnowball—but I did hear several talks on snow and balls during the Joint Math Meetings.
An invited address by Yuval Peres was followed by a session of six talks related in one way or another to the theme of diffusion-limited aggregation. This is a subject dear to me; the graphic in the bit-player heading is a product of a DLA simulation (see my old column on the topic).
The snowiest of the DLA talks was by Janko Gravner, whose work on snowfakes I have discussed before. I won’t say more here except to mention one illuminating offhand remark. In discussing Norman Packard’s cellular automaton for modeling snowflakes, Gravner quoted Steven Levy’s book Artificial Life:
An elementary schoolchild could look at any of the gorgeous pictures of computer screens in Packard’s collection and instantly identify it as a snowflake.
What the schoolchild would actually recognize, Gravner pointed out, is not a snowflake but “Christmas iconography.” And surely it’s true: We’ve all seen so many of those lacy doily patterns with hexagonal symmetry that we believe snowflakes really look like that. Some do, but many others are plates or needles or even wheel-and-axle assemblies.
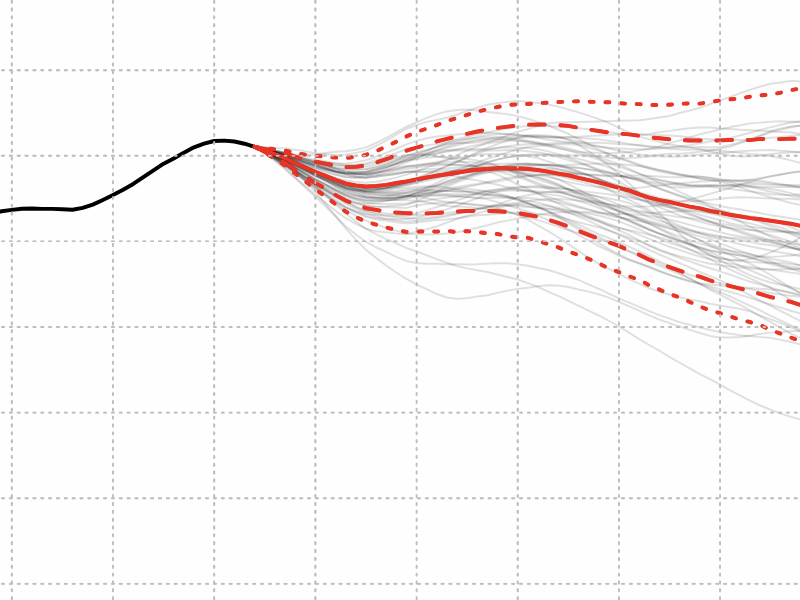
DLA is one way of modeling snowflake growth: Water-vapor molecules drift in from some distant source, wander randomly, and stick fast when they touch any part of the solid snowflake. The feathery patterns in the bit-player header were created by such an algorithm. But most of the talks in the JMM session concerned an inside-out version of this process: Particles (or “chips”) are released at the center and wander across the structure formed by the deposition of earlier chips, stopping as soon as they find a vacant site. What’s intriguing about this “interior” DLA is that the resulting shapes are not at all feathery or lacy. They are compact “blobs.” And if you let the process run long enough, the blob evolves into a ball, with a boundary approximating a circle.
Jim Propp invented a derandomized version of interior DLA called the rotor-router model. Each site in the lattice is equipped with an arrow, and when a chip reaches the site, it exits in the direction indicated by the arrow; then the arrow rotates by some fixed rule, such as turning 90 degrees clockwise. This scheme has many properties of a random walk—the chips are sent in all directions with equal probability—but it is fully deterministic. (Propp was one of the speakers in the DLA session. He promises to put his slides online, presumably here, but when I checked this morning they weren’t yet up.)
The rotor-router patterns are also round blobs, but in addition they have an intricate internal structure that becomes visible when the sites are colored according to the rotor-arrow direction. Tobias Friedrich, who gave another of the talks, has some spectacular examples on his web site. Using the technology of the Google Maps API, Friedrich’s site allows you to zoom into images of billion-pixel DLA patterns.
The big question is: Why so round? It’s not really surprising that the forms created in this was are generally compact, without the voids or branched structures seen in “external” DLA experiments. But the pure circular shape remains unexplained. In these models all the action takes place on a lattice—usually square, but triangular and hexagonal lattices have been tried as well—and you might expect some remnant of the lattice symmetry to show through in the deposited pattern. There’s no sign of it.
On the other hand, Matthew Cook, in the final talk of the session, revealed that although the blobs are very round indeed (within about a third of a pixel, on average), they are apparently not perfect circles. There are persistent bulges, not quite aligned with the lattice axes, that don’t seem to be smoothed away as the number of chips increases.
This is posted from the New Orleans airport, on my way back to the land of real snowflakes.