BP has finally stoppered the Macondo well with a plug of mud and cement, but the gusher of spam continues to pollute inboxes everywhere. Maybe we need a relief well?
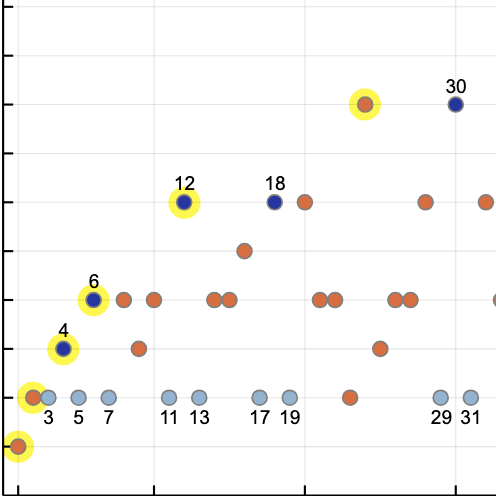
It’s been six months since my last spam update. The good news, I suppose, is that last summer’s huge spurt of spam has subsided. But I’m still getting 2,000 inanities a month. That’s six or seven times the rate I was seeing when I first started monitoring my spam intake in 2003. For the two years covered by the graph above, the cumulative total is 111,945 unwanted emails received.
Needless to say, most of those messages are utterly unremarkable. But as I reviewed the most recent batch of dreck, one series of emails caught my eye. In the past 24 hours I’ve received five copies of a spam with the subject line: “Solve this if you could…!!!!”:
For all Math’s champs, Accounting Experts & Number Numbssss… (including future champs too)
Find the 6th Number
1, 2, 6, 42, 1806, ____?
6th number is the password of the attachment.
The attachment mentioned in the last line is a zip archive that unpacks to reveal an .exe file, which I would not run even if I could. But I confess that I did stop to solve the little puzzle sequence. It’s not difficult, although it is a little harder than any of the series I use in the spambot filter on the bit-player comment form. Maybe I should add it to my repertory.
3263442
Normally, I get brain freeze on questions like this unless they’re pretty easy. I got this one in just a few seconds, so…?
3270666
The OEIS thinks different.
It would take us an average of 25 seconds longer to post comments :)
Time to try this on some Accounting Experts and Number Numbs, whoever those are.
Dave: same experience here, usually I have to try several things to get an answer but I spotted the pattern almost immediately.
Pattern recognition is so mysterious to me, I think I’ve found what I’m going to read about for the rest of the afternoon.
Okay, the math gene clearly skipped a generation. I have no idea what the answer to this problem is despite spending 15 minutes trying to figure it out. My only comfort is that two of the commenters came up with different responses.
The typical vanity of mathematicians - never apologise, never explain. I’m going to help out the lady by expanding on Dave of Tucson’s answer: 1×2, 2×3, 6×7, 42×43, 1806×1807 = 3263442. Now if only Mr and Mrs OEIS will be so good as to explain theirs. Of course a pattern can be completed in more than one way - it’s all a question of taste. Discrimination precedes measurement. And communication is a wonderful thing.
Fred Merk writes:
Obviously the correct response to this comment is enigmatic silence. But since I’m not actually a mathematician, I’m not required to observe all the usual vanities.
By way of explanation, if not apology, I would note that when someone has taken the initiative to go to work on a problem and has run into difficulties, simply giving away the answer is not often the most helpful response. Isn’t the process of finding the answer more important and more enjoyable than the answer itself? (In this case I happen to know through private back-channel communication that Amy Hayes did indeed solve the problem on her own shortly after posting her comment.)
As for the alternative solution offered by Mr and Mrs. OEIS, those who simply want to know the answer can run off to consult the OEIS. For those who would rather puzzle it out, I’ll offer one more term of the sequence as a hint:
1, 2, 6, 42, 1806, 3270666, 10697259354222,…
There is no ONE right answer to such questions, although there may be one, which seems most plausible to most people.
Any sequence of n numbers can be thought to be the values of polynome of degree below n with the independant variable x running from 0 (zero) to n-1. As such a next number can be developed as
p(n) — by the way without any multiplication, just additions and subtractions, unless one were interested in a closed form of the polynome.
By the same token one could choose ANY next number and have these n+1 numbers be generated by a polynome q of degree not above n — and upon being challenged for an algorithm by which this next number was got at, exhibit this polynome q.
What is the next number in the sequence 0,1,0,1, … ?
Of course it must be 8.
Or whatever you fancy.