It’s the nature of triangles that no one side can be longer than the sum of the other two sides: For triangle ABC, AC ≤ AB + BC. This is the triangle inequality. Euclid proved it (Book I, Proposition 20). With appropriate definitions it holds for triangles on the surface of a sphere as well as on a plane. And the everyday human experience of moving around in the universe amply confirms it. Unless you are booking a flight from Boston to Philadelphia.
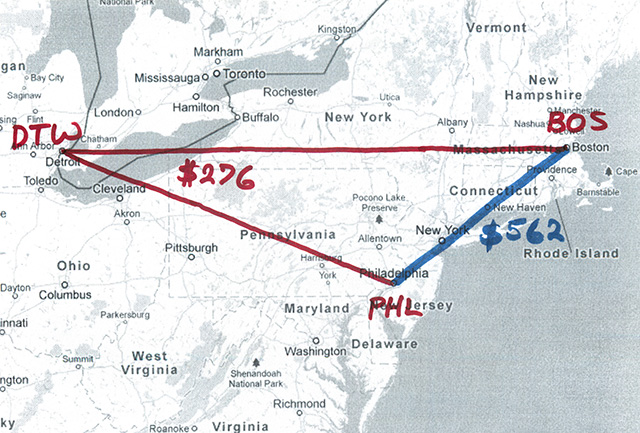
Yesterday I had to arrange such a trip on short notice. I was offered a choice of several direct flights, with the cheapest round-trip ticket priced at $562. But I could get there and back for just $276 if I went via Detroit.
I am fascinated and appalled by the economics of this situation. From one point of view it makes perfect sense: A direct flight is faster and more convenient, so of course it should command a premium price. But when you look at the cost side of the equation, it seems crazy: The Detroit detour quadruples the mileage and adds an extra takeoff and landing. Shouldn’t those flyers who long for a view of Lake Erie and a stopover in the Motor City be asked to pay extra for the privilege?
The usual explanation of this paradox is the marginal-cost argument. If the BOS-PHL route is saturated, but there are empty seats on the BOS-DTW and DTW-PHL legs, the airline is better off filling the vacant seats at any price above the marginal cost of adding a single passenger. If the price is too attractive, however, customers will defect from the premium flight. No doubt the observed price differential was determined by some optimization program running in the airline’s back office, nudging the system toward an equilibrium point.
Sound sensible? Suppose I had wanted to go to Detroit instead of Philadelphia. When I looked up the fares this morning, I found that the cheapest nonstop BOS-DTW ticket is $1,224. But I could pay as little as $578 if I were willing to make a detour through—guess where—Philadelphia. Now it appears the load factors are reversed: It’s the Beantown–Motown corridor where demand is strong, while the City of Brotherly Love takes up the slack.
If that program in the back office were trying to optimize overall system efficiency—perhaps aiming to minimize aggregate passenger travel time as well as fuel consumption, pollution, labor inputs and other resources—I have a hard time believing it would come up with a solution anything like the itinerary I’m following today.
By the way, I’m not going to Detroit. I’m making a stop in Queens instead. At least the triangle is skinnier.
Update: Totally triangular. On the first leg of the trip, we pushed away from the gate at Logan airport and the pilot immediate announced that we’d be waiting an hour or more before takeoff because of air traffic congestion at JFK. What could cause such congestion? You don’t suppose the problem might possibly be caused or exacerbated by pricing policies that encourage people flying from Boston to Philadelphia to stop in New York?
As it turned out, the delay was only 10 or 15 minutes rather than an hour, and I made my connection to the Philadelphia flight.
On the return trip, I was getting emails and phone messages from the airline as I waited barefoot in the security queue at PHL. My departure time had been pushed back by 30 minutes, again because of JFK congestion. When I got to the gate, a weary but helpful agent told me: “If you want to get home tonight, go to Cincinnati.” So I took the fat triangle, flying 1,244 miles to go just 268 (a worse ratio than the Detroit route).
Is all this just the whining of an unhappy traveler? Maybe, but I there’s an economic puzzle that I’m wanting to solve. What rational business strategy rewards a customer or a company for wasting 1,000 miles worth of fuel?