In an American Scientist column published last November, I discussed efforts by groups at Harvard and Yale to identify arrangements of n equal-size spheres that maximize the number of pairwise contacts between spheres. The Harvard collaboration (Natalie Arkus, Vinothan N. Manoharan and Michael P. Brenner) solved this problem for clusters of up to n = 10 spheres. The Yale group (Robert S. Hoy, Jared Harwayne-Gidansky and Corey S. O’Hern) extended the result to n = 11.
In describing some algorithmic refinements by the Yale researchers I wrote the following sentence:
For example, they took advantage of a curious fact proved by Therese Biedl, Erik Demaine and others: Any valid packing of spheres has a continuous, unbranched path that threads from one sphere to the next throughout the structure, like a long polymer chain.
A few weeks ago Robert Connelly of Cornell wrote me to point out that this statement is erroneous in two ways. First, Biedl and Demaine and their colleagues did not prove (or even attempt to prove) the “curious fact” I mentioned. Second, the fact is not a fact. It’s simply not true that all “valid packings” have a continuous unbranched path from sphere to sphere—known as a Hamiltonian path, after William Rowan Hamilton.
What’s a “valid packing”? The Harvard and Yale groups focused on arrangements of spheres that meet two criteria: A cluster must have at least 3n – 6 sphere-to-sphere contacts overall, and every sphere must touch at least three other spheres. Clusters that satisfy these conditions are termed “minimally rigid.” Connelly showed that not all such clusters have a Hamiltonian path. The demonstration is direct. Working with Erik Demaine and Martin Demaine, he produced a counterexample—a 16-sphere minimally rigid cluster that can be proved to have no Hamiltonian path. It later emerged there is a smaller example, with just 14 spheres.
The concept of a Hamiltonian path comes from graph theory rather than geometry, but it’s easy to translate between the two realms. The spheres of a geometric cluster correspond to the vertices of a graph; two vertices in the graph are connected by an edge if and only if the corresponding spheres are in contact. A Hamiltonian path through the graph is a route along some subset of the edges that visits each vertex exactly once. A graph that has such a path is said to be traceable, since you can follow the route through a diagram without ever lifting the pencil. The Hamiltonian path is not required to traverse all the edges. Nor does it have to return to its starting point. (A path that does form a closed loop is a called a Hamiltonian circuit.)
Connelly’s 16-sphere counterexample is shown in the photographs below as a skeleton built with the Geomags construction kit. At right is the corresponding graph, with edge colors that match those in the photos.


A 16-sphere cluster that has no Hamiltonian path is shown in equatorial and polar views. In this Geomags model, the sphere centers are represented by the shiny steel balls; spheres in contact are connected by a colored magnetic strut. All the struts are the same length. The graph at right preserves the pattern of connectivity of the cluster but not the geometry.
The core of this structure (yellow) is a pentagonal dipyramid with 10 triangular faces. Nine of the faces are decorated with tetrahedral caps (red); the tenth face is left unadorned. Counting the balls and struts in the model or the vertices and edges in the graph shows that the structure satisfies the criteria for minimal rigidity: The 16 spheres are linked by 3 × 16 – 6 = 42 bonds, and every sphere touches at least three others.
How do we know that the graph has no Hamiltonian path? In general, answering this question is a difficult task (indeed, it’s NP-complete). But this particular graph was designed specifically to make the problem easy. Connelly explains why there can be no unbranched path that threads through all the vertices:
The reason is a simple counting argument. Suppose there is a Hamiltonian path. Since there are 16 vertices in all, the Hamiltonian path must have 15 edges. Each of the 9 additional vertices is adjacent to 2 edges in the Hamiltonian path, except possibly for the 2 end points of the path, which each correspond to 1 edge of the path. This is a disjoint set of at least 2 × 9 – 2 = 16 edges, one more than there are in the path, a contradiction.
The smaller, 14-sphere counterexample is constructed in the same way, but instead of a pentagonal dipyramid the core of the structure is a square dipyramid—an object better known as an octahedron. All eight faces are capped with tetrahedra, making a stellate octahedron.
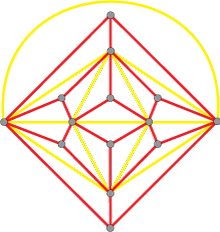

The argument for the impossibility of a Hamiltonian path takes exactly the same form as in Connelly’s example. Any path that reaches all eight of the stellate vertices must include at least 2 × 8 – 2 = 14 edges, but a Hamiltonian path in this graph has only 13 edges.

The illustration at left is another representation of the stellate octahedron, this time as a packing of equal-size spheres. (If you hover your mouse over the image, it might spin.)
The procedure for creating these non-Hamiltonian structures was devised by the geometer Victor Klee; the resulting figures are now called Kleetopes. The 14-node octahedral example, which Klee mentions in Branko Grünbaum’s book Convex Polytopes, is the smallest of an infinite series. You might think you could produce an even smaller example by starting with a triangular dipyramid, which has five vertices and six triangular faces. Adding six tetrahedral caps yields a cluster with 11 vertices in all. However, this structure does have Hamiltonian paths. (On the other hand, it has no Hamiltonian circuit.)
When we give up the erroneous assumption that all minimally rigid arrangements have Hamiltonian paths, what is the status of the two searches for high-contact-number sphere packings? The following assessment is based on conversations and correspondence with several of the participants, but the wording and the conclusions are mine; others might well see it differently.
First of all, the Harvard group did not rely on any assumptions about Hamiltonian paths, so their enumeration of clusters up to n = 10 is entirely unaffected.
The Yale group adopted the Hamiltonian-path assumption as a way of containing the combinatorial explosion when they extended the search to n = 11. The computational burden can be measured in terms of the number of graph adjacency matrices, \(\bar{A}\), that need to be examined. Hoy, Harwayne-Gidansky and O’Hern wrote:
All macrostates can be found with greatly reduced computational effort through appropriate selection of “topological” constraints on the elements of \(\bar{A}\). Biedl et al. . . . proved that all connected sphere packings admit linear polymeric paths, that is, for any valid packing, one can always permute particle indices so that the packing is fully traversed by a “polymeric” \(\bar{A}\) with \(A_{i,i+1} = 1\) for all \(i\).
This assumption that all entries on the superdiagonal of the matrix can be set equal to 1 brings a huge reduction in computational cost. For n = 11, the number of matrices to be considered is slashed by more than three orders of magnitude. But of course that means 99.9 percent of all the candidate matrices are passed over without examination. If any of those ignored matrices were valid minimally rigid packings of 11 spheres, the Yale survey would have missed them.
How much should we worry about this potential omission? It depends on your point of view. If you look upon the result as a mathematical proof classifying all minimally rigid sphere clusters, then the proof has a big gap. But, as I noted in my American Scientist column, mathematical rigor was not the highest priority in this work and was already jeopardized by the use of a numerical algorithm (Newton’s method) that is not guaranteed to converge in all cases. The original motivation for both the Harvard and Yale projects came from chemistry and physics, not from geometry and graph theory. The idea was to identify the kinds of clusters that might form nuclei of condensing crystals or aggregations of colloidal particles. The physical significance of the findings is not much compromised by doubts about mathematical rigor.
In any case, the Yale results will require revision only if there exists at least one minimally rigid cluster of 11 or fewer spheres without a Hamiltonian path—and that now seems unlikely. Any such cluster with n ≤ 10 would have been found by the Harvard survey (which, again, did not exclude untraceable graphs). Meanwhile, recent work by Miranda Holmes-Cerfon of NYU has produced a new enumeration of sphere packings up to n = 12. The full results are still unpublished but she reports no sign of clusters that were missed because of the incorrect Hamiltonian-path assumption.
The Holmes-Cerfon survey is based on a different methodology. Instead of generating vast numbers of adjacency matrices and testing them to see which ones correspond to valid packings, she begins with a known cluster and tries to transform it into all other valid packings with the same number of spheres. The transformations consist of all possible movements of a single bond that maintain the conditions for minimal rigidity. This process is computationally less arduous, although it does rely on the assumption that all valid configurations can be reached by some series of single-bond moves.
When I first heard about the search for clusters that maximize contact number, I was surprised to learn that such simple questions remain unanswered. How could it be that we know so little about clusters of just a dozen spheres? I’m still intrigued, and now I have another question to noodle over: How come we know so little about Hamiltonian paths in small graphs? Is Klee’s 14-vertex example the smallest for minimally rigid structures? There can’t be any efficient way of answering this question (unless P = NP), but is it beyond our ability to close the gap between n = 11 and n = 14?
Acknowledgments: I’m grateful to Bob Connelly both for bring this matter to my attention and for helping me understand the issue. I have also benefitted from very helpful conversations and emails with Natalie Arkus, Michael P. Brenner, Karoly Bezdek, Miranda Holmes-Cerfon, Robert Hoy, David Wales and Zorana Zeravcic. (But if I still don’t have the story straight, it’s not their fault!)