When the Wordle wave washed over the world some months ago, I played along like everybody else, once a day collecting my rows of gray and gold and green letters. But my main interest was not in testing my linguistic intuitions; I wanted to write a computer program to solve the puzzle. Could I create something that would play a stronger game than I do? It’s now clear the answer to that question is yes, but I can’t say whether it’s because I’m such a hotshot programmer or such a mediocre Wordler.
I hasten to add that my motivation in this project is not to cheat. Josh Wardle, the creator of Wordle, took all the fun out of cheating by making it way too easy. Anybody can post impressive results like this one:

That lonely row of green squares indicates that you’ve solved the puzzle with a single brilliant guess. The Wordle app calls that performance an act of “Genius,” but if it happens more than once every few years, your friends may suspect another explanation.
The software I’ve written will not solve today’s puzzle for you. You can’t run the program unless you already know the answer. Thus the program won’t tell you, in advance, how to play; but it may tell you, retrospectively, how you should have played.
The aim in Wordle is to identify a hidden five-letter word. When you make a guess, the Wordle app gives you feedback by coloring the letter tiles. A green tile indicates that you have put the right letter in the right place.
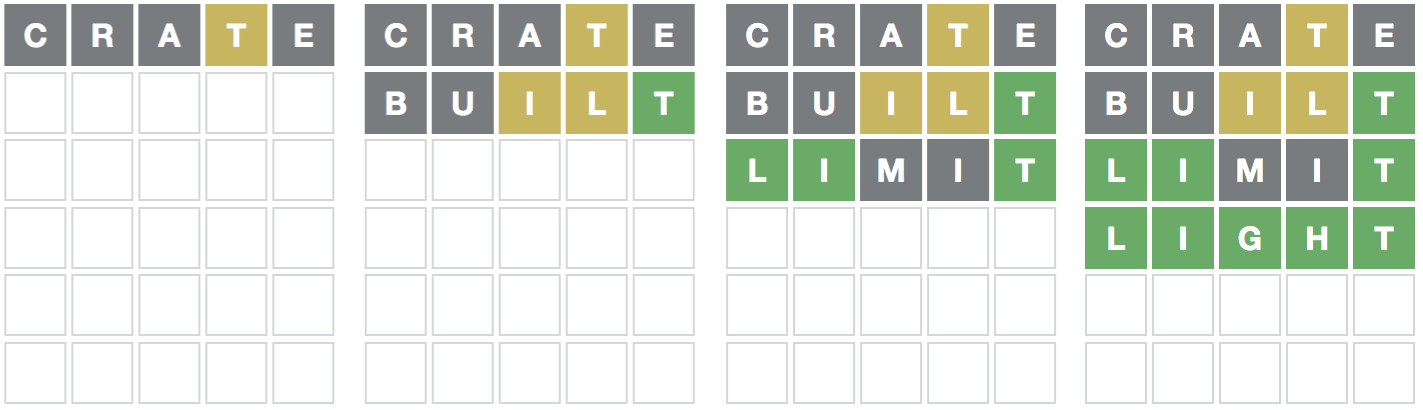
The sequence of grids above records the progress of a game I played several weeks ago. The initial state of the puzzle is a blank grid with space for six words of five letters each. My first guess, CRATE (far left), revealed that the letter T is present in the target word, but not in the fourth position; the other letters, CRAE, are absent. I then played BUILT and learned where the T goes, and that the letters I and L are also present. The third guess, LIMIT, got three letters in their correct positions, which was enough information to rule out all but one possibility. The four green tiles in row four confirm that LIGHT is the target word.
The official Wordle app gives you six chances to guess the Wordle-of-the-day. If you fill the grid with six wrong answers, the game ends and the app reveals the word you failed to find.
It’s important to bear in mind that Wordle is played in a closed universe.
Both of the word lists are downloaded to your web browser whenever you play the game, and you can examine or copy them by peeking at the JavaScript source code with your browser’s developer tools.
Conceptually, a Wordle-playing program conducts a dialogue between two computational agents: the Umpire and the Player. The Umpire knows the target word, and responds to submitted guess words in much the same way the Wordle app does. It marks each of the five letters in the guess as either correct, present, or absent, corresponding to the Wordle color codes of green, gold, and gray.
The Player component of the program does not know the target word, but it has access to the lists of common and arcane words. On each turn, the Player selects a word from one of these lists, submits it to the Umpire, and receives feedback classifying each of the letters as correct, present, or absent. This information can then be used to help choose the next guess word. The guessing process continues until the Player identifies the target word or exhausts its six turns.
Here’s a version of such a program. Type in a start word and a target word, then press Go. Briefly displayed in gray letters are the words the program evaluates as possible next guesses. The most promising candidate is then submitted to the Umpire and displayed with the green-gold-gray color code.
Feel free to play with the buttons below the grid. The “?” button will pop up a brief explanation. If you’d like to peek behind the curtain, the source code for the project is available on GitHub. Also, a standalone version of the program may be more convenient if you’re reading on a small screen.
This program is surely not the best possible Wordler, but it’s pretty good. Most puzzle instances are solved in three or four guesses. Failures to finish within six guesses are uncommon if you choose a sensible starting word. The algorithms behind Program 1 will be the main subject of this essay, but before diving into them I would like to consider some simpler approaches to playing the game.
When I first set out to write a Wordler program, I chose the easiest scheme I could think of. At the start of a new game, the Player chooses a word at random from the list of 2,315 potential target words. (The arcana will not be needed in this program.) After submitting this randomly chosen word as a first guess, the Player takes the Umpire’s feedback report and uses it to sift through the list of potential targets, retaining those words that are still viable candidates and setting aside all those that conflict in some way with the feedback. The Player then selects another word at random from among the surviving candidates, and repeats the process. On each round, the list of candidates shrinks further.
The winnowing of the candidate list is the heart of the algorithm. Suppose the first guess word is COULD, and the Umpire’s evaluation is equivalent to this Wordle markup: ![]() . You can now go through the list of candidate words and discard all those that have a letter other than L in the fourth position. You can also eliminate all words that include any instance of the letters C, U, or D. The gold letter O rules out all words in two disjoint classes: those that don’t have an O anywhere in their spelling, and those that do have an O in the second position. After this winnowing process, only seven words remain as viable candidates.
. You can now go through the list of candidate words and discard all those that have a letter other than L in the fourth position. You can also eliminate all words that include any instance of the letters C, U, or D. The gold letter O rules out all words in two disjoint classes: those that don’t have an O anywhere in their spelling, and those that do have an O in the second position. After this winnowing process, only seven words remain as viable candidates.
One aspect of these rules often trips me up when I’m playing. Wordle is not Wheel of Fortune: The response to a guess word might reveal that the target word has an L, but it doesn’t necessarily show you all the Ls. If you play COULD and get the feedback displayed above, you should not assume that the green L in the fourth position is the only L. The target word could be ATOLL, HELLO, KNOLL, or TROLL. (When both the guess and the target words have multiple copies of the same letter, the rules get even trickier. If you want to know the gory details, see Note 2.)
The list-winnowing process is highly effective. Even with a randomly chosen starter word, the first guess typically eliminates more than 90 percent of the target words, leaving only about 220 viable candidates, on average. In subsequent rounds the shrinkage is not as rapid, but it’s usually enough to identify a unique solution within the allotted six guesses.
I wrote the random Wordler as a kind of warmup exercise, and I didn’t expect much in the way of performance. Plucking words willy-nilly from the set of all viable candidates doesn’t sound like the shrewdest strategy. However, it works surprisingly well. The graph below shows the result of running the program on each of the 2,315 target words, with the experiment repeated 10,000 times to reduce statistical noise.
Guess pool: remaining target words
Start word: randomly chosen
The average number of guesses needed to find the solution is 4.11, and only 2 percent of the trials end in failure (requiring seven or more guesses).
Incidentally, this result is quite robust, in the sense that the outcome doesn’t depend at all on the composition of the words on the target list. If you replace the official Wordle list with 2,315 strings of random letters, the graph looks the same.
The surprising strength of a random player might be taken as a sign that Wordle isn’t really a very hard game. If you are guided by a single, simple rule—play any word that hasn’t already been excluded by feedback from prior guesses—you will win most games. From another point of view the news is not so cheering: If a totally mindless strategy can often solve the puzzle in four moves, you may have to work really hard to do substantially better.
Still another lesson might be drawn from the success of the random player: The computer’s complete ignorance of English word patterns is not a major handicap and might even be an advantage. A human player’s judgment is biased by ingrained knowledge of differences in word frequency. If I see the partial solution BE _ _ _, I’m likely to think first of common words such as BEGIN and BENCH, rather than the rarer BELLE and BEZEL. In the Wordle list of potential targets, however, each of these words occurs with exactly the same frequency, namely 1/2315. A policy favoring common words over rare ones is not helpful in this game.
But a case can be made for a slightly different strategy, based on a preference not for common words but for common letters. A guess word made up of high-frequency letters should elicit more information than a guess consisting of rare letters. By definition, the high-frequency letters are more likely to be present in the target word. Even when they are absent, that fact becomes valuable knowledge. If you make JIFFY your first guess and thereby learn that the target word does not contain a J, you eliminate 27 candidates out of 2,315. Playing EDICT and learning that the target has no E rules out 1,056 words.
The table below records the number of occurrences of each letter from A to Z in all the Wordle target words, broken down according to position within the word. For example, A is the first letter of 141 target words, and Z is the last letter of four words.
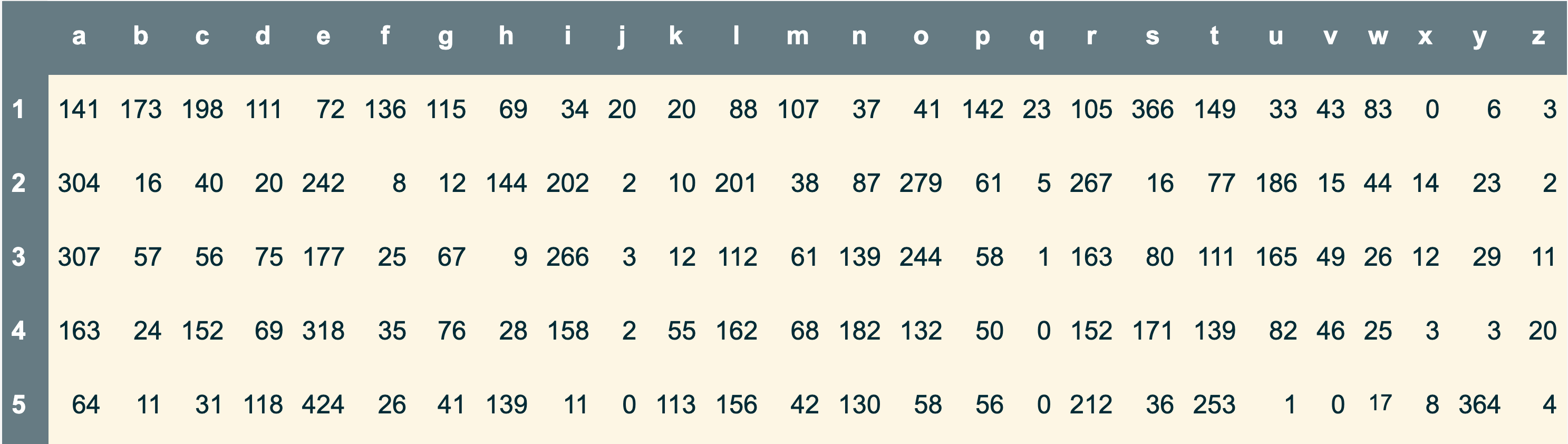
The same information is conveyed in the heatmap below, where lighter colors indicate more common letters.
These data form the basis of another Wordle-playing algorithm. Given a list of candidate words, we compute the sum of each candidate’s letter frequencies, and select the word with the highest score. For example, the word SKUNK gets 366 points for the initial S, then 10 points for the K in the second position, and so on through the rest of the letters for an aggregate score of 366 + 10 + 165 + 182 + 113 = 836. SKUNK would win over KOALA, which has a score of 832, but lose to PIGGY (851).
Testing the letter-frequency algorithm against all 2,315 target words yields this distribution of results:
Guess pool: remaining target words
Start word: determined by algorithm (SLATE)
The mean number of guesses is 3.83, noticeably better than the random-choice average of 4.11. The failure rate—words that aren’t guessed within six turns—is pushed down to 1.1 percent (28 out of 2,315).
There’s surely room for improvement in the letter-frequency algorithm. One weakness is that it treats the five positions in each word as independent variables, whereas in reality there are strong correlations between each letter and its neighbors. For example, the groups CH, SH, TH, and WH are common in English words, and Q is constantly clinging to U. Other pairs such as FH and LH are almost never seen. These attractions and repulsions between letters play a major role in human approaches to solving the Wordle puzzle (or at least they do in my approach). The letter-frequency program could be revised to take advantage of such knowledge, perhaps by tabulating the frequencies of bigrams (two-letter combinations). I have not attempted anything along these lines. Other ideas hijacked my attention.
Like other guessing games, such as Bulls and Cows, Mastermind, and Twenty Questions, Wordle is all about acquiring the information needed to unmask a hidden answer. Thus if you’re looking for guidance on playing the game, an obvious place to turn is the body of knowledge known as information theory, formulated 75 years ago by Claude Shannon.
Shannon’s most important contribution (in my opinion) was to establish that information is a quantifiable, measurable substance. The unit of measure is the bit, defined as the amount of information needed to distinguish between two equally likely outcomes. If you flip a fair coin and learn that it came up heads, you have acquired one bit of information.
This scheme is easy to apply to the game of Twenty Questions, where the questions are required to have just two possible answers—yes or no. If each answer conveys one bit of information, 20 questions yield 20 bits, which is enough to distinguish one item among \(2^{20} \approx 1\) million equally likely possibilties. In general, if a collection of things has \(N\) members, then the quantity of information needed to distinguish one of its members is the base-2 logarithm of \(N\), written \(\log_2 N\).
In Wordle we ask no more than six questions, but answers are not just yes or no. Each guess word is a query submitted to the Umpire, who answers by coloring the letter tiles. There are more than two possible answers; in fact, there are 243 of them. As a result, a Wordle guess has the potential to yield much more than one bit of information. But there’s also the possibility of getting less than one bit.
Where does that curious number 243 come from? In the Umpire’s response to a guess, each letter is assigned one of three colors, and there are five letters in all. Hence the set of all possible responses has \(3^5 = 243\) members. Here they are, in all their polychrome glory:
These color codes represent every feedback message you could ever possibly receive when playing Wordle. (And then some! The five codes outlined in pink can never occur. Note 2 explains why.) Each color pattern can be represented as a five-digit numeral in ternary (base-3) notation, with the digit 0 signifying gray or absent, 1 indicating gold or present, and 2 corresponding to green or correct. Because these are five-digit numbers, I’ve taken to calling them Zip codes. The all-gray 00000 code at the upper left appears in the Wordle grid when your guess has no letters in common with the target word. A solid-green 22222, at the bottom right, marks the successful conclusion of a game. In the middle of the grid is the all-gold 11111, which is reserved for “deranged anagrams”:
When you play a guess word in Wordle, you can’t know in advance which of the 243 Zip codes you’ll receive as feedback, but you can know the spectrum of possibilities for that particular word. Program 2,
Each of the slender bars that grow from the baseline of the chart represents a single Zip-code, from all-gray at the far left, through all-gold in the middle, and on to all-green at the extreme right. ![]() and
and ![]() get the same color in the bar chart.
get the same color in the bar chart.
The pattern of short and tall bars in Program 2 is something like an atomic spectrum for Wordle queries. Each guess word generates a unique pattern. A word like MOMMY or JIFFY yields a sparse distribution, with a few very tall bars and wide empty spaces between them. The sparsest of all is QAJAQ (a word on the arcane list that seems to be a variant spelling of KAYAK): All but 18 of the 243 Zip codes are empty. Words such as SLATE, CRANE, TRACE, and RAISE, on the other hand, produce a dense array of shorter bars, like a lush carpet of grass, where most of the categories are occupied by at least one target word.
Can these spectra help us solve Wordle puzzles? Indeed they can! The guiding principle is simple: Choose a guess word that has a “flat” spectrum, distributing the target words uniformly across the 243 Zip codes. The ideal is to divide the set of candidate words into 243 equal-size subsets. Then, when the Umpire’s feedback singles out one of these categories for further attention, the selected Zip code is sure to have relatively few occupants, making it easier to determine which of those occupants is the target word. In this way we maximize the expected information gain from each guess.
This advice to spread the target words broadly and thinly across the space of Zip codes may seem obvious and in no need of further justification. If you feel that way, read on. Those who need persuading (as I did) should consult Note 3.
The ideal of distributing words with perfect uniformity across the Wordle spectrum is, lamentably, unattainable. None of the 12,972 available query words achieves this goal. The spectra all have lumps and bumps and bare spots. The best we can do is choose the guess that comes closest to the ideal. But how are we to gauge this kind of closeness? What mathematical criterion should we adopt to compare those thousands of spiky spectra?
Information theory again waves its hand to volunteer an answer, promising to measure the number of bits of information one can expect to gain from any given Wordle spectrum. The tool for this task is an equation that appeared in Shannon’s 1948 paper “A Mathematical Theory of Communication.” I have taken some liberties with the form of the equation, adapting it to the peculiarities of the Wordle problem and also trying to make its meaning more transparent. For the mathematical details see Note 4.
Here’s the equation in my preferred format:
\[H_w = \sum_{\substack{i = 1\\n_i \ne 0}}^{242} \frac{n_i}{m} (\log_2 m - \log_2 n_i) .\]
\(H_w\), the quantity we are computing, is the amount of information we can expect to acquire by playing word \(w\) as our next guess.
On the righthand side of the equation we sum contributions from all the occupied Zip codes in \(w\)’s Wordle spectrum. The index \(i\) on the summation symbol \(\Sigma\) runs from 0 to 242 (which is 00000 to 22222 in ternary notation), enumerating all the Zip codes in the spectrum. The variable \(n_i\) is the number of target words assigned to Zip code \(i\), and \(m\) is the total number of target words included in the spectrum. At the start of the game, \(m = 2{,}315\), but after each guess it gets smaller.
Now let’s turn to the expression in parentheses. Here \(\log_2 m\) is the amount of information—the number of bits—needed to distinguish the target word among all \(m\) candidates. Likewise \(\log_2 n_i\) is the number of bits needed to pick out a single word from among the \(n_i\) words in Zip code \(i\). The difference between these quantities, \(\log_2 m - \log_2 n_i\), is the amount of information we gain if Zip code \(i\) turns out to be the correct choice—if it harbors the target word and is therefore selected by the Umpire.
Perhaps a numerical example will help make all this clearer. If \(m = 64\), we have \(\log_2 m = 6\): It would take 6 bits of information to single out the target among all 64 candidates. If the target is found in Zip code \(i\) and \(n_i = 4\), we still need \(\log_2 4 = 2\) bits of information to pin down its identity. Thus in going from \(m = 64\) to \(n_i = 4\) we have gained \(6 - 2 = 4\) bits of information.
So much for what we stand to gain if the target turns out to live in Zip code \(i\). We also have to consider the probability of that event. Intuitively, if there are more words allocated to a Zip code, the target word is more likely to be among them. The probability is simply \(n_i / m\), the fraction of all \(m\) words that land in code \(i\). Hence \(n_i / m\) and \(\log_2 m - \log_2 n_i\) act in opposition. Piling more words into Zip code \(i\) increases the probability of finding the target there, but it also increases the difficulty of isolating the target among the \(n_i\) candidates.
Each Zip code makes a contribution to the total expected information gain; the contribution of Zip code \(i\) is equal to the product of \(n_i / m\) and \(\log_2 m - \log_2 n_i\). Summing the contributions coming from all 243 categories yields \(H_w\), the amount of information we can expect to gain from playing word \(w\).
In case you find programming code more digestible than either equations or words, here is a JavaScript function for computing \(H_w\). The argument spectrum is an array of 243 numbers representing counts of words assigned to all the Zip codes.
function entropy(spectrum) {
const nzspectrum = spectrum.filter(x => x > 0);
const m = sum(spectrum);
let H = 0;
for (let n of spectrum) {
H += n/m * (log2(m) - log2(n));
}
return H;
}
In Program 2, this code calculates the entropy value labeled \(H\) in the Statistics panel. The same function is invoked in Program 1 when the “Maximize entropy” algorithm is selected.
Before leaving this topic behind, it’s worth pausing to consider a few special cases. If \(n_i = 1\) (i.e., there’s just a single word in Zip code \(i\)), then \(\log_2 n_i = 0\), and the information gain is simply \(\log_2 m\); we have acquired all the information we need to solve the puzzle. This result makes sense: If we have narrowed the choice down to a single word, it has to be the target. Now suppose \(n_i = m\), meaning that all the candidate words have congregated in a single Zip code. Then we have \(\log_2 m - \log_2 n_i = 0\), and we gain nothing by choosing word \(w\). We had \(m\) candidates before the guess, and we still have \(m\) candidates afterward.
What if \(n_i = 0\)—that is, Zip code \(i\) is empty? spectrum.filter(x => x > 0) does the same thing. This exclusion does no harm because if \(n_i\) is zero, then \(n_i / m\) is also zero, meaning there’s no chance that category \(i\) holds the winner. (If a Zip code has no words at all, it can’t have the winning word.)
\(H_w\) attains its maximum value when all the \(n_i\) are equal. As mentioned above, there’s no word \(w\) that achieves this ideal, but we can certainly calculate how many bits such a word would produce if it did exist. In the case of a first guess, each \(n_i\) must equal \(2315 / 243 \approx 9.5\), and the total information gain is \(\log_2 2315 - \log_2 9.5 \approx 7.9\) bits. This is an upper bound for a Wordle first guess; it’s the most we could possibly get out of the process, even if we were allowed to play any arbitrary string of five letters as a guess. As we’ll see below, no real guess gains as much as six bits.
These mathematical tools of information theory suggest a simple recipe for a Wordle-playing computer program. At any stage of the game the word to play is the one that elicits the most information about the target. We can estimate the information yield of each potential guess by computing its Wordle spectrum and applying the \(H_w\) equation to the resulting sequence of numbers. That’s what the JavaScript code below does.
function maxentropy(guesswordlist, targetwordlist) {
maxH = 0
bestguessword = ""
for (g in guesswordlist) { // outer loop
spectrum = []
for t in targetwordlist { // inner loop
zipcode = score(g, t)
spectrum(zipcode) += 1
}
H = entropy(spectrum)
if (H > maxH) {
maxH = H
bestguessword = g
}
}
return bestguessword
}In this function the outer loop visits all the guess words; then for each of these words the inner loop sifts through all the potential target words, constructing a spectrum. When the spectrum for guess word g is complete, the entropy procedure computes the information H to be gained by playing word w. The maxH and bestguessword variables keep track of the best results seen so far, and ultimately bestguessword is returned as the result of the function.
This procedure can be applied at any stage of the Wordling process, from the first guess to the last. When choosing the first guess—the word to be entered in the blank grid at the start of the game—all 2,315 common words are equally likely potential targets. We also have 12,972 guess words to consider, drawn from both the common and arcane lists. Calculating the information gain for each such starter word reveals that the highest score goes to SOARE, at 5.886 bits. (SOARE is apparently either a variant spelling of SORREL, a reddish-brown color, or an obsolete British term for a young hawk.) ROATE, a variant of ROTE, and RAISE are not far behind. At the bottom of the list is the notorious QAJAQ, providing just 1.892 bits of information.
Adopting SOARE as a starter word, we can then play complete games of Wordle with this algorithm, recording the number of guesses required to find all 2,315 target words. The result is a substantial improvement over the random and the letter-frequency methods.
Guess pool: common and arcane
Start word: SOARE
The average number of guesses per game is down to about 3.5, and almost 96 percent of all games are won in either three or four guesses. Only one target word requires six guesses, and there are no lost games, requiring seven or more guesses. As a device for Wordling, Shannon’s information theory is quite a success!
Shannon’s entropy equation was explicitly designed for the function it performs here—finding the distribution with maximum entropy. But if we consider the task more broadly as looking for the most widely dispersed and most nearly uniform distribution, other approaches come to mind. For example, a statistician might suggest variance or standard deviation as an alternative to Shannon entropy. The standard deviation is defined as:
\[\sigma = \sqrt{\frac{\Sigma_i (n_i - \mu)^2}{N}},\]
where \(\mu\) is the average of the \(n_i\) values and \(N\) is the number of values. In other words, we are measuring how far the individual elements of the spectrum differ from the average value. If the target words were distributed uniformly across all the Zip codes, every \(n_i\) would be equal to \(\mu\), and the standard deviation \(\sigma\) would be zero. A large \(\sigma\) indicates that many \(n_i\) differ greatly from the mean; some Zip codes must be densely populated and others empty or nearly so. Our goal is to find the guess word whose spectrum has the smallest possible standard deviation.
In the Wordling program, it’s an easy matter to substitute minimum standard deviation for maximum entropy as the criterion for choosing guess words. The JavaScript code looks like this:
function stddev(spectrum) {
const mu = sum(spectrum) / 243;
const diffs = spectrum.map(x => x - mu);
const variance = sum(diffs.map(x => x * x)) / 243;
return Math.sqrt(variance);
}In Program 1, you can see the standard deviation algorithm in action by selecting the button labeled “Minimum std dev.” In Program 2, standard deviation values are labeled \(\sigma\) in the Statistics panel.
Testing the algorithm with all possible combinations of a starting word and a target word reveals that the smallest standard deviation is 22.02, and this figure is attained only by the spectrum of the word ROATE. Not far behind are RAISE, RAILE, and SOARE. At the bottom of the list, the worst choice by this criterion is IMMIX, with \(\sigma = 95.5\).
Using ROATE as the steady starter word, I ran a full set of complete games, surveying the standard-deviation program’s performance across all 2,315 target words. I was surprised at the outcome. Although the chart looks somewhat different—more 4s, fewer 3s—the average number of guesses came within a whisker of equalling the max-entropy result: 3.54 vs. 3.53. Of particular note, there are fewer words requiring five guesses, and a few more are solved with just two guesses.
Guess pool: common and arcane
Start word: ROATE
Why was I surprised by the strength of the standard-deviation algorithm? Well, as I said, Shannon’s \(H\) equation is a tool designed specifically for this job. Its mathematical underpinnings assert that no other rule can extract information with greater efficiency. That property seems like it ought to promise superior performance in Wordle. Standard deviation, on the other hand, is adapted to problems that take a different form. In particular, it is meant to measure dispersion in distributions with a normal or Gaussian shape. There’s no obvious reason to expect Wordle spectra to follow the normal law. Nevertheless, the \(\sigma\) rule is just as successful in choosing winners.
Following up on this hint that the max-entropy algorithm is not the only Wordle wiz, I was inspired to try a rule even simpler than standard deviation. In this algorithm, which I call “max scatter,” we choose the guess word whose spectrum has the largest number of occupied Zip codes. In other words, we count the bars that sprout up in Program 2, but we ignore their height. In the Statistics panel of Program 2, the max-scatter results are designated by the letter \(\chi\) (Greek chi), which I chose by analogy with the indicator function of set theory. In Program 1, choose “Maximize scatter” to Wordle this way.
If we adopt the \(\chi\) standard, the best first guess in Wordle is TRACE, which scatters target words over 150 of the 243 Zip codes. Other strong choices are CRATE and SALET (148 codes each) and SLATE and REAST (147). The bottom of the heap is good ole QAJAQ, with 18.
Using TRACE as the start word and averaging over all target words, the performance of the scatter algorithm actually exceeds that of the max-entropy program. The mean number of guesses is 3.49. There are no failures requiring 7+ guesses, and only one target word requires six guesses.
Guess pool: common and arcane
Start word: TRACE
What I find most noteworthy about these results is how closely the programs are matched, as measured by the average number of guesses needed to finish a game. It really looks as if the three criteria are all equally good, and it’s a matter of indifference which one you choose. This (tentative) conclusion is supported by another series of experiments. Instead of starting every game with the word that appears best for each algorithm, I tried generating random pairs of start words and target words, and measured each program’s performance for 10,000 such pairings. Having traded good start words for randomly selected ones, it’s no surprise that performance is somewhat weaker across the board, with the average number of guesses hovering near 3.7 instead of 3.5. But all three algorithms continue to be closely aligned, with figures for average outcome within 1 percent. And in this case it’s not just the averages that line up; the three graphs look very similar, with a tall peak at four guesses per game.
As I looked at these results, it occurred to me that the programs might be so nearly interchangeable for a trivial reason: because they are playing identical games most of the time. Perhaps the three criteria are similar enough that they often settle on the same sequence of guess words to solve a given puzzle. This does happen: There are word pairs that elicit exactly the same response from all three programs. It’s not a rare occurrence. But there are also plenty of examples like the trio of game grids in Figure 11, where each program discovered a unique pathway from FALSE to VOWEL.
A few further experiments show that the three programs arrive at three distinct solutions in about 35 percent of random games; in the other 65 percent, at least two of the three solutions are identical. In 20 percent of the cases all three are alike. Figure 12 shows the relevant statistics for a sample of 5,000 games with random pairings of start and target words. (The notation \(H =\sigma =\chi\) refers to outcomes in which all programs yield the same result. In \(H \ne\sigma \ne\chi\) the three solutions are all distinct. The other three bars count individual pairwise matches.) The result for \(\sigma = \chi\) is a curiosity I don’t understand. It seems those two programs almost never agree unless \(H\) also concurs.
I puzzled over these observations for some time. If the algorithms discover wholly different paths through the maze of words, why are those paths so often the same length? I now have a clue to an answer, but it may not be whole story, and I would welcome alternative explanations.
My mental model of what goes on inside a Wordling program runs like this: The program computes the spectrum of each word to be considered as a potential guess, then computes some function—\(H\), \(\sigma\), or \(\chi\)—that reduces the spectrum to a single number. The number estimates the expected quality or efficiency of the word if it is taken as the next guess in the game. Finally we choose the word that either maximizes or minimizes this figure of merit (the word with largest value of \(H\) or \(\chi\), or the smallest value of \(\sigma\)).
So far so good, but there’s an unstated assumption in that scheme: I take it for granted that evaluating the spectra will always yield a single, unique extreme value of \(H\), \(\sigma\), or \(\chi\). What happens if two words are tied for first place? One could argue, of course, that if the words earn the same score, they must be equally good choices, and we should pick one of them at random or by some arbitrary rule. Even if there are three or four or a dozen co-leaders, the same reasoning should apply. But when there are two thousand words all tied for first place, I’m not so sure.
Can such massive traffic jams at the finish line actually happen in a real game of Wordle? At first I didn’t even consider the possibility. When I rated all possible starting words for the Shannon max-entropy algorithm, the ranking turned out to be a total order: In the list of 12,792 words there were no ties—no pairs of words whose spectra have the same \(H\) value. Hence there’s no ambiguity about which word is best, as measured by this criterion.
But this analysis applies only to the opening play—the choice of a first guess, when all the common words are equally likely to be the target. In the endgame the situation is totally different. Suppose the list of 2,315 common words has been whittled down to just five viable candidates for Wordle-of-the-day. When the five target words are sorted into Zip-code categories and the entropy of these patterns is calculated (excluding empty Zip codes), there are only seven possible outcomes, as shown in Figure 13. The patterns correspond to the seven ways of partitioning the number 5 (namely 5, 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, and 1+1+1+1+1).
In this circumstance, the 12,972 guess words cannot all have unique values of \(H\). On the contrary, with only seven distinct values to go around, there must be thousands of tie scores in the ranking of the words. Thus the max-entropy algorithm cannot pick a unique winner; instead it assembles a large class of words that, from the program’s point of view, are all equally good choices. Which of those words ultimately becomes the next guess is more or less arbitrary. For the most part, my programs pick the one that comes first in alphabetical order.
The same arguments apply to the minimum-standard-deviation algorithm. As for the max-scatter function, that has numerous tied scores even when the number of candidates is large. Because the variable \(\chi\) takes on integer values in the range from 1 to 243 (and in practice never strays outside the narrower range 18 to 150), there’s no avoiding an abundance of ties.
The presence of all these co-leaders offers an innocent explanation of how the three algorithms might arrive at solutions that are different in detail but generally equal in quality. Although the programs pick different words, those words come from the same equivalence class, and so they yield equally good outcomes.
But a doubt persists. Can it really be true that hundreds or thousands of words are all equally good guesses in some Wordle positions? Can you choose any one of those words and expect to finish the game in the same number of plays?
Let’s go back to Figure 11, where the maximum-entropy program follows the opening play of FALSE with DETER and then BINGO. Some digging through the entrails of the program reveals that BINGO is not the uniquely favored guess at this point in the progress of the game; VENOM, VINYL, and VIXEN are tied with BINGO at \(H = 3.122\) bits. The program chooses BINGO simply because it comes first alphabetically. As it happens, the choice is an unfortunate one. Any of the other three words would have concluded the game more quickly, in four guesses rather than five.
Does that mean we now have unequivocal evidence that the program is suboptimal? Not really. At the stage of the game where BINGO was chosen, there were still 10 viable possibilities for the target word. The true target might have been LIBEL, for example, in which case BINGO would have been superior to VENOM or VIXEN.
Human players see Wordle as a word game. What else could it be? To solve the puzzle you scour the dusty corners of your vocabulary, searching for words that satisfy certain constraints or fit a given template. You look for patterns of vowels and consonants and other curious aspects of English orthography.
For the algorithmic player, on the other hand, Wordle is a numbers game. What counts is maximizing or minimizing some mathematical function, such as entropy or standard deviation. The words and letters all but disappear.
The link between words and numbers is the Umpire’s scoring rule, with the spectrum of Zip codes that comes out of it. Every possible combination of a guess word and a target word gets reduced to a five-digit ternary number. Instead of computing each of these numbers as the need arises, we can precompute the entire set of Zip codes and store it in a matrix. The content of the matrix is determined by the letters of the words we began with, but once all the numbers have been filled in, we can dispense with the words themselves. Operations on the matrix depend only on the numeric indices of the columns and rows. We can retrieve any Zip code by a simple table lookup, without having to think about the coloring of letter tiles.
In exploring this matrix, let’s set aside the arcana for the time being and work only with common words. With 2,315 possible guesses and the same number of possible targets, we have \(2{,}315^2 \approx 5.4\) million pairings of a guess and a target. Each such pairing gets a Zip code, which can be represented by a decimal integer in the range from 0 to 242. Because these small numbers fit in a single byte of computer memory, the full matrix occupies about five-and-a-half megabytes.
Figure 14 is a graphic representation of the matrix. Each column corresponds to a guess word, and each row to a target word. The words are arranged in alphabetical order from left to right and top to bottom. The matrix element where a column intersects a row holds the Zip code for that combination. The color scheme is the same as in Program 2. The main diagonal (upper left to lower right) is a bright green stripe because each word when played against itself gets a score of 22222, equivalent to five green tiles. The blocks of lighter green all along the diagonal mark regions where guess words and target words share the same first letter and hence have scores with at least one green tile. The largest of these blocks is for words beginning with the letter S. A few other blocks are quite tiny, reflecting the scarcity of words beginning with J, K, Q, Y, and Z. A box for X is lacking entirely; the Wordle common list has no words beginning with X.

Gazing deeply into the tweedy texture of Figure 14 reveals other curious structures, but some features are misleading. The matrix appears to be symmetric across the main diagonal: The point at (a, b) always has the same color as the point at (b, a). But the symmetry is an artifact of the graphic presentation, where colors are assigned based only on the number of gray, gold, and green tiles, ignoring their positions within a word. The underlying mathematical matrix is not symmetric.
I first built this matrix as a mere optimization, a way to avoid continually recomputing the same Zip codes in the course of a long series of Wordle games. But I soon realized that the matrix is more than a technical speed boost. It encapsulates pretty much everything one might want to know about the entire game of Wordle.
Figure 15 presents a step-by-step account of how matrix methods lead to a Wordle solution. In the first stage (upper left) the player submits an initial guess of SLATE, which singles out column 1778 in the matrix (1778 being the position of SLATE in the alphabetized list of common words). The second stage (upper right) reveal’s the Umpire’s feedback, coloring the tiles as follows: ![]() . To the human solver this message would mean: “Look for words that have an S (but not in front) and a T (but not in fourth position).” To the computer program the message says: “Look for rows in the matrix whose 1778th entry is equal to 10010 (base 3) or 84 (base 10). It turns out there are 24 rows meeting this condition, which are highlighted in blue. (Some lines are too closely spaced to be distinguished.) I have labeled the highlighted rows with the words they represent, but the labels are for human consumption only; the program has no need of them.
. To the human solver this message would mean: “Look for words that have an S (but not in front) and a T (but not in fourth position).” To the computer program the message says: “Look for rows in the matrix whose 1778th entry is equal to 10010 (base 3) or 84 (base 10). It turns out there are 24 rows meeting this condition, which are highlighted in blue. (Some lines are too closely spaced to be distinguished.) I have labeled the highlighted rows with the words they represent, but the labels are for human consumption only; the program has no need of them.
In the third panel (lower left), the program has chosen a second guess word, TROUT, which earns the feedback ![]() . I should mention that this is not a word I would have considered playing at this point in the game. The O and U make sense, because the first guess eliminated A and E and left us in need of a vowel; but the presence of two Ts seems wasteful. We already know the target word has a T, and pinning down where it is seems less important than identifying the target word’s other constituent letters. I might have tried PROUD here. Yet TROUT is a brilliant move! It eliminates 7 words that start with T, 12 words that don’t have an R, 17 words that have either an O or a U or both, and 4 words that don’t end in T. In the end only one word remains in contention: FIRST.
. I should mention that this is not a word I would have considered playing at this point in the game. The O and U make sense, because the first guess eliminated A and E and left us in need of a vowel; but the presence of two Ts seems wasteful. We already know the target word has a T, and pinning down where it is seems less important than identifying the target word’s other constituent letters. I might have tried PROUD here. Yet TROUT is a brilliant move! It eliminates 7 words that start with T, 12 words that don’t have an R, 17 words that have either an O or a U or both, and 4 words that don’t end in T. In the end only one word remains in contention: FIRST.
All this analysis of letter positions goes on only in my mind, not in the algorithm. The computational process is simpler. The guess TROUT designates column 2118 of the matrix. Among the 24 rows identified by the first guess, SLATE, only row 743 has the Zip code value 01002 (or 29 decimal) at its intersection with column 2118. Row 743 is the row for FIRST. Because it is the only remaining viable candidate, it must be the target word, and this is confirmed when it is played as the third guess (lower right).
There’s something disconcerting—maybe even uncanny—about a program that so featly wins a word game while ignoring the words. Indeed, you can replace all the words in Wordle with utter gibberish—with random five-letter strings like SCVMI, AHKZB, and BOZPA—and the algorithm will go on working just the same. It has to work a little harder—the average number of guesses is near 4—but a human solver would find the task almost impossible.
The square matrix of Figure 14 includes only the common words that serve as both guesses and targets in Wordle. Including the arcane words expands the matrix to 12,972 columns, with a little more than 30 million elements. At low resolution this wide matrix looks like this:

If you’d like to see all 30 million pixels up close and personal, download the 90-megabyte TIFF image.
Commentators on Wordle have given much attention to the choice of a first guess: the start word, the sequence of letters you type when facing a blank grid. At this point in the game you have no clues of any kind about the composition of the target word; all you know is that it’s one of 2,315 candidates. Because this list of candidates is the same in every game, it seems there might be one universal best starter word—an opening play that will lead to the smallest average number of guesses, when the average is taken over all the target words. Furthermore, because 2,315 isn’t a terrifyingly large number, a brute-force search for that word might be within the capacity of a less-than-super computer.
Start-word suggestions from players and pundits are a mixed lot. A website called Polygon offers some whimsical ideas, such as FARTS and OUIJA. GameRant also has oddball options, including JUMBO and ZAXES. Tyler Glaiel offers better advice, reaching deep into the arcana to come up with SOARE and ROATE. Grant Sanderson skillfully deduces that CRANE is the best starter, then takes it all back.
For each of the algorithms I have mentioned above (except the random one) the algorithm itself can be pressed into service to suggest a starter. For example, if we apply the max-entropy algorithm to the entire set of potential guess words, it picks out the one whose spectrum has the highest \(H\) value. As I’ve already noted, that word is SOARE, with \(H = 5.886\). Table 1 gives the 15 highest-scoring choices, based on this kind of analysis, for the max-entropy, min–standard deviation and max-scatter algorithms.
First-Move Starter-Word Rankings
| Max Entropy | |
|---|---|
| SOARE | 5.886 |
| ROATE | 5.883 |
| RAISE | 5.878 |
| RAILE | 5.866 |
| REAST | 5.865 |
| SLATE | 5.858 |
| CRATE | 5.835 |
| SALET | 5.835 |
| IRATE | 5.831 |
| TRACE | 5.831 |
| ARISE | 5.821 |
| ORATE | 5.817 |
| STARE | 5.807 |
| CARTE | 5.795 |
| RAINE | 5.787 |
| Min Std Dev | |
|---|---|
| ROATE | 22.02 |
| RAISE | 22.14 |
| RAILE | 22.22 |
| SOARE | 22.42 |
| ARISE | 22.72 |
| IRATE | 22.73 |
| ORATE | 22.76 |
| ARIEL | 23.05 |
| AROSE | 23.20 |
| RAINE | 23.41 |
| ARTEL | 23.50 |
| TALER | 23.55 |
| RATEL | 23.97 |
| AESIR | 23.98 |
| ARLES | 23.98 |
| Max Scatter | |
|---|---|
| TRACE | 150 |
| CRATE | 148 |
| SALET | 148 |
| SLATE | 147 |
| REAST | 147 |
| PARSE | 146 |
| CARTE | 146 |
| CARET | 145 |
| PEART | 145 |
| CARLE | 144 |
| CRANE | 142 |
| STALE | 142 |
| EARST | 142 |
| HEART | 141 |
| REIST | 141 |
Perusing these lists reveals that they all differ in detail, but many of the same words appear on two or more lists, and certains patterns turn up everywhere. A disproportionate share of the words have the letters A, E, R, S, and T; and half the alphabet never appears in any of the lists.
Figure 17 looks at the distribution of starter quality ratings across the entire range of potential guess words, both common and arcane. The 12,972 starters have been sorted from best to worst, as measured by the max-entropy algorithm. The plot gives the number of bits of information gained by playing each of the words as the initial guess, in each case averaging over all 2,315 target words.
The peculiar shape of the curve tells us something important about Wordling strategies. A small subset of words in the upper left corner of the graph make exceptionally good starters. In the first round of play they elicit almost six bits of information, which is half of what’s needed to finish the game. At the other end of the curve, a slightly larger cohort of words produce really awful results as starters, plunging down to the 1.8 bits of QAJAQ. In between these extremes, the slope of the curve is gradual, and there are roughly 10,000 words that don’t differ greatly in their performance.
These results might be taken as the last word on first words, but I would be a cautious about that. The methodology makes an implicit “greedy” assumption: that the strongest first move will always lead to the best outcome in the full game. It’s rather like assuming that the tennis player with the best serve will always win the match. Experience suggests otherwise. Although a strong start is usually an advantage, it’s no guarantee of victory.
We can test the greedy assumption in a straightforward if somewhat laborious way: For each proposed starter word, we run a complete set of 2,315 full games—one for each of the target words—and we keep track of the average number of guesses needed to complete a game. Playing 2,315 games takes a few minutes for each algorithm; doing that for 12,792 starter words exceeds the limits of my patience. But I have compiled full-game results for 30 starter words, all of them drawn from near the top of the first-round rankings.
Table 2 gives the top-15 results for each of the algorithms. Comparing these lists with those of Table 1 reveals that first-round supremacy is not in fact a good predictor of full-game excellence. None of the words leading the pack in the first-move results remain at the head of the list when we measure the outcomes of complete games.
Full-Game Starter-Word Rankings
| Max Entropy | |
|---|---|
| REAST | 3.487 |
| SALET | 3.492 |
| TRACE | 3.494 |
| SLATE | 3.495 |
| CRANE | 3.495 |
| CRATE | 3.499 |
| SLANE | 3.499 |
| CARTE | 3.502 |
| CARLE | 3.503 |
| STARE | 3.504 |
| CARET | 3.505 |
| EARST | 3.511 |
| SNARE | 3.511 |
| STALE | 3.512 |
| TASER | 3.514 |
| Min Std Dev | |
|---|---|
| TRACE | 3.498 |
| CRATE | 3.503 |
| REAST | 3.503 |
| SALET | 3.508 |
| SLATE | 3.508 |
| SLANE | 3.511 |
| CARTE | 3.512 |
| CARLE | 3.516 |
| CRANE | 3.517 |
| CARSE | 3.523 |
| STALE | 3.524 |
| CARET | 3.524 |
| STARE | 3.525 |
| EARST | 3.527 |
| SOREL | 3.528 |
| Max Scatter | |
|---|---|
| SALET | 3.428 |
| REAST | 3.434 |
| CRANE | 3.434 |
| SLATE | 3.434 |
| CRATE | 3.435 |
| TRACE | 3.435 |
| CARLE | 3.437 |
| SLANE | 3.438 |
| CARTE | 3.444 |
| STALE | 3.450 |
| TASER | 3.450 |
| CARET | 3.451 |
| EARST | 3.452 |
| CARSE | 3.453 |
| STARE | 3.454 |
What’s the lesson here? Do I recommend that when you get up in the morning to face your daily Wordle, you always start the game with REAST or TRACE or SALET or one of the other words near the top of these lists? That’s not bad advice, but I’m not sure it’s the best advice. One problem is that each of these algorithms has its own favored list of starting words. Your own personal Wordling algorithm—whatever it may be—might respond best to some other, idiosyncratic, set of starters.
Moreover, my spouse, who Wordles and Quordles and Octordles and Absurdles, reminds me gently that it’s all a game, meant to be fun, and some people may find that playing the same word day after day gets boring.
Figure 18 presents the various algorithms at their shiny best, each one using the starter word that brings out its best performance. For comparison I’ve also included my own Wordling record, based on 126 games I’ve played since January. I’m proud to say that I Wordle better than a random number generator.
I turn now from the opening move to the endgame, which I find the most interesting part of Wordle—but also, often, the most frustrating. It seems reasonable to say that the endgame begins when the list of viable targets has been narrowed down to a handful, or when most of the letters in the target are known, and only one or two letters remain to be filled in.
Occasonally you might find yourself entering the endgame on the very first move. There’s the happy day when your first guess comes up all green—an event I have yet to experience. Or you might have a close call, such as playing the starter word EIGHT and getting this feedback: ![]() . Having scored four green letters, it looks like you’ve got an easy win. With high hopes, you enter a second guess of FIGHT, but again you get the same four greens and one gray. So you type out LIGHT next, and then MIGHT. After two more attempts, you are left with this disappointing game board:
. Having scored four green letters, it looks like you’ve got an easy win. With high hopes, you enter a second guess of FIGHT, but again you get the same four greens and one gray. So you type out LIGHT next, and then MIGHT. After two more attempts, you are left with this disappointing game board:

What seemed like a sure win has turned into a wretched loss. You have used up your six turns, but you’ve not found the Wordle-of-the-day. Indeed, there are still three candidate targets yet to be tried: SIGHT, TIGHT, and WIGHT.
The _ IGHT words are by no means the only troublemakers. Similar families of words match the patterns _ ATCH, _ OUGH, _ OUND, _ ASTE and _ AUNT. You can get into even deeper endgame woes when an initial guess yields three green tiles. For example, 12 words share the template S_ _ ER, 25 match _ O_ ER, and 29 are consistent with _ A_ ER.
These sets of words are challenging not only for the human solver but also, under some circumstances, for Wordling algorithms. In Program 1, choose the word list “Candidates only” and then try solving the puzzle for target words such as FOYER, WASTE, or VAUNT. Depending on your starter word, you are likely to see the program struggle through several guesses, and it may fail to find the answer within six tries.
The “Candidates only” setting requires the program to choose each guess from the set of words that have not yet been excluded from consideration as the possible target. For example, if feedback from an earlier guess has revealed that the target ends in T and has an I, then every subsequent guess must end in T and have an I. (Restricting guesses to candidates only is similar to the Wordle app’s “hard mode” setting, but a little stricter.)
Compelling the player to choose guesses that might be winners doesn’t seem like much of a hardship or handicap. However, trying to score a goal with every play is seldom the best policy. Other guesses, although they can’t possibly be winners, may yield more information.
An experienced and wordly-wise human Wordler, on seeing the feedback ![]() , would know better than to play for an immediate win. The prudent strategy is play a word that promises to reveal the identity of the one missing letter. Here’s an example of how that works.
, would know better than to play for an immediate win. The prudent strategy is play a word that promises to reveal the identity of the one missing letter. Here’s an example of how that works.



At left the second-guess FLOWN detects the presence of a W, which means the target can only be WIGHT. In the middle, FLOWN reveals only absences, but the further guess MARSH finds an S, which implies the target must be SIGHT. At right, the second and third guesses have managed to eliminate F, L, W, N, M, R, and S as initial letters, and all that’s left is the T of TIGHT.
This virtuoso performance is not the work of some International Grandmaster of Wordling. It is produced by the max-entropy algorithm, when the program is allowed a wider choice of potential guesses. The standard-deviation and max-scatter algorithms yield identical results. There is no special logic built into any of these programs for deciding when to play to win and when to hunker down and gather more information. It all comes out of the Zip code spectrum: FLOWN and MARSH are the words that maximize \(H\) and \(\chi\), and that minimize \(\sigma\). And yet, when you watch the game unfold, it looks mysterious or magical.
The cautious strategy of accumulating intelligence before committing to a line of play yields better results on average, but it comes with a price. All of the best algorithms achieve their strong scores by reducing the number of games that linger for five or six rounds of guessing. However, those algorithms also reduce the number of two-guess games, an effect that has to be counted as collateral damage. Two-guess triumphs make up less than 3 percent of the games played by the Zip code–based programs. Contrast that with the letter-frequency algorithm: In most respects it is quite mediocre, but it wins more than 6 percent of its games in two guesses. And among my personal games, 7 percent are two-guess victories. (I don’t say this to brag; what it suggests is that my style of play is a tad reckless.)
The Zip code–based programs would have even fewer two-guess wins without a heuristic that improves performance in a small fraction of cases. Whenever the list of candidate target words has dwindled down to a length of two, there’s no point in seeking more information to distinguish between the two remaining words. Suppose that after the first guess you’re left with the words SWEAT and SWEPT as the only candidates. For your second guess you could play a word such as ADEPT, where either the A or the P would light up to indicate which candidate is the target. You would then have a guaranteed win in three rounds. But if you simply played one of the candidate words as your second guess, you would have a 50 percent chance of winning in two rounds, and otherwise would finish in three, for an average score of 2.5.
This heuristic is already implemented in the programs discussed above. It makes a noticeable difference. Removing it from the max-entropy program drops the number of two-guess games from 51 down to 35 (out of 2,315).
Can we go further with this idea? Suppose there are three candidates left as you’re preparing for the second round of guessing. The cautious, information-gathering strategy would bring consistent victory on the third guess. Playing one of the candidates leads to a game that lasts for two, three, or four turns, each with probability one-third, so the average is again three guesses. The choice appears to be neutral. In practice, playing one of the candidates brings a tiny improvement in average score—too tiny to be worth the bother.
Another optimization says you should always pick one of the remaining candidates for your sixth guess. Gathering additional information is pointless in this circumstance, because you’ll never have a chance to use it. However, the better algorithms almost never reach the sixth guess, so this measure has no payoff in practice.
Apart from minor tricks and tweaks like these, is there any prospect of building significantly better Wordling programs? I have no doubt that improvement is possible, even though all my own attempts to get better results have failed miserably.
Getting to an average performance of 3.5 guesses per game seems fairly easy; getting much beyond that level may require new ideas. My impression is that existing methods work well for choosing the first guess and perhaps the second, but are less effective in closing out the endgame. When the number of candidates is small, the Zip code–based algorithms cannot identify a single best next guess; they merely divide the possibilities into a few large classes of better and worse guesses. We need finer means of discrimination. We need tiebreakers.
I’ll briefly mention two of my failed experiments. I thought I would try going beyond the Zip code analysis and computing for each combination of a guess word and a potential target word how much the choice would shrink the list of candidates. After all, the point of the game is to shrink that list down to a single word. But the plague of multitudinous ties afflicts this algorithm too. Besides, it’s computationally costly.
Another idea was to bias the ranking of the Zip code spectra, favoring codes that have more gold and green letter tiles, on the hypothesis that we learn more when a letter is present or correct. The hypothesis is disproved! Even tiny amounts of bias are detrimental.
My focus has been on reducing the average number of guesses, but maybe there are other goals worth pursuing. For example, can we devise an algorithm that will solve every Wordle with no more than four guesses? It’s not such a distant prospect. Already there are algorithms that exceed four guesses only in about 2 percent of the cases.
Perhaps progress will come from another quarter. I’ve been expecting someone to put one of the big machine-learning systems to work on Wordle. All I’ve seen so far is a small-scale study, based on the technique of reinforcement learning, done by Benton J. Anderson and Jesse G. Meyer. Their results are not impressive, and I am led to wonder if there’s something about the problem that thwarts learning techniques just as it does other algorithmic approaches.
Wordle falls into the class of combinatorial word games. All you need to know is how letters go together to make a word; meaning is beside the point. Most games of this kind are highly susceptible to computational force majeure. A few lines of code and a big word list will find exhaustive solutions in milliseconds. For example, another New York Times game called Spelling Bee asks you to make words out of seven given letters, with one special letter required to appear in every word. I’m not very good at Spelling Bee, but my computer is an ace. The same code would solve the Jumble puzzles on the back pages of the newspaper. With a little more effort the program could handle Lewis Carroll’s Word Links (better known today as Don Knuth’s Word Ladders). And it’s a spiffy tool for cheating at Scrabble.
In this respect Wordle is different. One can easily write a program that plays a competent game. Even a program that chooses words at random can turn in a respectable score. But this level of proficiency is nothing like the situation with Spelling Bee or Jumble, where the program utterly annihilates all competition, leaving no shred of the game where the human player could cling to claims of supremacy. In Wordle, every now and then I beat my own program. How can that happen, in this day and age?
The answer might be as simple and boring as computational complexity. If I want my program to win, I’ll have to invest more CPU cycles. Or there might be a super-clever Wordle-wrangling algorithm, and I’ve just been too dumb to find it. Then again, there might be something about Wordle that sets it apart from other combinatorial word games. That would be interesting.
Notes
Note 1. History of the game and of the word lists.
The charming story of Wordle’s creation was told last January in the New York Times. “Wordle Is a Love Story” read the headline. Josh Wardle, a software developer formerly at Reddit, created the game as a gift to his partner, Palak Shah, a fan of word games. The Times story, written by Daniel Victor, marvelled at the noncommercial purity of the website: “There are no ads or flashing banners; no windows pop up or ask for money.” Three weeks later the Times bought the game, commenting in its own pages, “The purchase . . . reflects the growing importance of games, like crosswords and Spelling Bee, in the company’s quest to increase digital subscriptions to 10 million by 2025.” So much for love stories.
As far as I can tell, the new owners have not fiddled with the rules of the game, but there have been a few revisions to the word lists. Here’s a summary based on changes observed between February and May.
Six words were removed from the list of common words (a.k.a. target words), later added to the list of arcane words, then later still removed from that list as well, so that they are no longer valid as either a guess or a target:
AGORA, PUPAL, LYNCH, FIBRE, SLAVE, WENCH
Twenty-two words were moved from various positions in the common words list to the end of that list (effectively delaying their appearance as Wordle-of-the-day until sometime in 2027):
BOBBY, ECLAT, FELLA, GAILY, HARRY, HASTY, HYDRO,
LIEGE, OCTAL, OMBRE, PAYER, SOOTH, UNSET, UNLIT,
VOMIT, FANNY, FETUS, BUTCH, STALK, FLACK, WIDOW,
AUGUR
Two words were moved forward from near the end of the common list to a higher position where they replaced FETUS and BUTCH:
SHINE, GECKO
Two words were removed from the arcane list and not replaced:
KORAN, QURAN
Almost all the changes to the common list affect words that would have been played at some point in 2022 if they had been left in place. I expect further purges when the editors get around to vetting the rest of the list.
Note 2. The Umpire’s scoring rule.
When I first started playing Wordle, I had a simple notion of what the tile colors meant. If a tile was colored green, then that letter of the guess word appeared in the same position in the target word. A gold tile meant the letter would be found elsewhere in the target word. A gray tile indicated the letter was entirely absent from the target word. For my first Wordler program I wrote a procedure implementing this scheme, although its output consisted of numbers rather than colors: green = 2, gold = 1, gray = 0.
function scoreGuess(guess, target)
score = [0, 0, 0, 0, 0]
for i in 1:5
if guess[i] == target[i]
score[i] = 2
elseif occursin(guess[i], target)
score[i] = 1
end
end
return score
endThis rule and its computer implementation work correctly as long as we never apply them to words with repeated letters. But suppose the target word is MODEM and you play the guess MUDDY. Following the rule above, the Umpire would offer this feedback: ![]() . Note the gold coloring of the second D. It’s the correct marking according to the stated rule, because the target word has a D not in the fourth position. But that D in MODEM is already “spoken for”; it is matched with the green D in the middle of MUDDY. The gold coloring of the second D could be misleading, suggesting that there’s another D in the target word.
. Note the gold coloring of the second D. It’s the correct marking according to the stated rule, because the target word has a D not in the fourth position. But that D in MODEM is already “spoken for”; it is matched with the green D in the middle of MUDDY. The gold coloring of the second D could be misleading, suggesting that there’s another D in the target word.
The Wordle app would color the second D gray, not gold: ![]() . The rule, apparently, is that each letter in the target word can be matched with only one letter in the guess word. Green matches take precedence.
. The rule, apparently, is that each letter in the target word can be matched with only one letter in the guess word. Green matches take precedence.
There remains some uncertainty about which letter gets a gold score when there are multiple options. If MUDDY is the target word and ADDED is the guess word, we know that middle D will be colored green, but which of the other two Ds in ADDED gets a gold tile? I have not been able to verify how the Wordle app handles this situation, but my program assigns priority from left to right: ![]() .
.
This minor amendment to the rules brings a considerable cost in complexity to the code. We need an extra data structure (the array tagged) and an extra loop. The first loop (with index i) finds and marks all the green matches; the second loop (indices j and k) identifies gold tiles that have not been preempted by earlier green or gold matches.
function scoreGuess(guess, target)
score = [0, 0, 0, 0, 0]
tagged = [0, 0, 0, 0, 0]
for i in 1:5
if guess[i] == target[i]
score[i] = 2
tagged[i] = 2
end
end
for j in 1:5
for k in 1:5
if guess[j] == target[k] && score[j] == 0 && tagged[k] == 0
score[j] = 1
tagged[k] = 1
end
end
end
return score
endIt is this element of the scoring rules that forbids Zip codes such as ![]() and its permutations in Figure 6. Under the naive rules, the guess STALL played against the target STALE would have been scored
and its permutations in Figure 6. Under the naive rules, the guess STALL played against the target STALE would have been scored ![]() . The refined rule renders it as
. The refined rule renders it as ![]() .
.
Note 3. The virtues of a uniform distribution.
Let’s think about a game that’s simpler than Wordle, though doubtless less fun to play. You are given a deck of 64 index cards, each with a single word written on it; one of the words, known only to the Umpire, is the target. Your instructions are to “cut” the deck, dividing it into two heaps. Then the all-seeing Umpire will tell you which heap includes the target word. For the next round of play, you set aside the losing heap, and divide the winning heap into two parts; again the Umpire indicates which pile holds the winning word. The process continues until the heap approved by the Umpire consists of a single card, which must necessarily be the target. The question is: How many rounds of play will it take to reach this decisive state?
If you always divide the remaining stack of cards into two equal heaps, this question is easy to answer. On each turn, the number of cards and words remaining in contention is cut in half: from 64 to 32, then on down to 16, 8, 4, 2, 1. It takes six halvings to resolve all uncertainty about the identity of the target. This bisection algorithm is a central element of information theory, where the fundamental unit of measure, the bit, is defined as the amount of information needed to choose between two equally likely alternatives. Here the choices are the two heaps of equal size, which have the same probability of holding the target word. When the Umpire points to one heap or the other, that signal provides exactly one bit of information. To go all the way from 64 equally likely candidates to one identified target takes six rounds of guessing, and six bits of information.
Bisection is known to be an optimal strategy for many problem-solving tasks, but the source of its strength is sometimes misunderstood. What matters most is not that we split the deck into two parts but that we divide it into equal subsets. Suppose we cut a pack of 64 cards into four equal heaps rather than two. When the Umpire points to the pile that includes the target, we get twice as much information. The search space has been reduced by a factor of four, from 64 cards to 16. We still need to acquire a total of six bits to solve the problem, but because we are getting two bits per round, we can do it in three splittings rather than six. In other words, we have a tradeoff between more simple decisions and fewer complex decisions.
Figure 21 illustrates the nature of this tradeoff by viewing a decision process as traversing a tree from the root node (at the top) to one of 16 leaf nodes (at the bottom). For the binary tree on the left, finding your way from the root to a leaf requires making four decisions, in each case choosing one of two paths. In the quaternary tree on the right, only two decisions are needed, but there are four options at each level. Assuming a four-way choice “costs” twice as much as a two-way choice, the information content is the same in both cases: four bits.
But what if we decide to split the deck unevenly, producing a larger and a smaller heap? For example, a one-quarter/three-quarter division would yield a pile of 16 cards on the left and 48 cards on the right. If the target happens to lie in the smaller heap, we are better off than we would be with an even split: We’ve gained two bits of information instead of one, since the search space has shrunk from 64 cards to 16. However, the probability of this outcome is only 1/4 rather than 1/2, and so our expected gain is only one bit. When the target card is in the larger pile, we acquire less than one bit of information, since the search space has fallen from 64 cards only as far as 48, and the probability of this event is 3/4. Averaging across the two possible outcomes, the loss outweighs the gain.
Figure 22 shows the information budget for every possible cut point in a deck of 64 cards. The red curves labeled left and right show the number of bits obtained from each of the two piles as their size varies. (The x axis labels the size of the left pile; wherever the left pile has \(n\) cards, the right pile has \(64 - n\).) The overarching green curve is the sum of the left and right values. Note that the green curve has its peak in the center, where the deck has been split into two equal subsets of 32 cards each. This is the optimum strategy.
I have made this game go smoothly by choosing 64 as the number of cards in the deck. Because 64 is a power of 2, you can keep dividing by 2 and never hit an odd number until you come to 1. With decks of other sizes the situation gets messy; you can’t always split the deck into two equal parts. Nevertheless, the same principles apply, with some compromises and approximations. Suppose we have a deck of 2,315 cards, each inscribed with one of the Wordle common words. (The deck would be about two feet high.) We repeatedly split it as close to the middle as possible, allowing an extra card in one pile or the other when necessary. Eleven bisections would be enough to distinguish one card out of \(2^{11} = 2{,}048\), which falls a little short of the goal. With 12 bisections we could find the target among \(2^{12} = 4{,}096\) cards, which is more than we need. There’s a mathematical function that interpolates between these fenceposts: the base-2 logarithm. Specifically, \(\log_2 2{,}315\) is about 11.18, which means the amount of information we need to solve a Wordle puzzle is 11.18 bits. (Note that \(2^{11.18} \approx 2315\). Of the 2,315 positions where the target card might lie within the deck, 1,783 are resolved in 11 bisections, and 532 require a 12th cut.)
Note 4. Understanding the Shannon entropy equation.
The foundational document of information theory, Claude Shannon’s 1948 paper “A Mathematical Theory of Communication,” gives the entropy equation is this form:
\[H = -\sum_{i} p_i \log_2 p_i .\]
The equation’s pedigree goes back further, to Josiah Willard Gibbs and Ludwig Boltzmann, who introduced it in a different context, the branch of physics called statistical mechanics.
Over the years I’ve run into this equation many times, but I do not count it among my close friends. Whenever I come upon it, I have to stop and think carefully about what the equation means and how it works. The variable \(p_i\) represents a probability. We are asked to multiply each \(p_i\) by the logarithm of \(p_i\), then sum up the products and negate the result. Why would one want to do such a thing? What does it accomplish? How do these operations reveal something about entropy and information?
When I look at the righthand side of the equation, I see an expression of the general form \(n \log n\), which is a familiar trope in several areas of mathematics and computer science. It generally denotes a function that grows faster than linear but slower than quadratic. For example, sorting \(n\) items might require \(n \log n\) comparison operations. (For any \(n\) greater than 2, \(n \log_2 n\) lies between \(n\) and \(n^2\).)
That’s not what’s going on here. Because \(p\) represents a probability, it must lie in the range \(0 \le p \le 1\). The logarithm of a number in this range is negative or at most zero. This gives \(p \log p\) a different complexion. It also draws attention to that weird minus sign hanging out in front of the summation symbol.
I believe another form of the equation is easier to understand, even though the transformation introduces more bristly mathematical notation. Let’s begin by moving the minus sign from outside to inside the summation, attaching it to the logarithmic factor:
\[H = \sum_{i} p_i (-\log_2 p_i) .\]
The rules for logarithms and exponents tell us that \(-\log x = \log x^{-1}\), and that \(x^{-1} = 1/x\). We can therefore rewrite the equation again as
\[H = \sum_{i} p_i \log_2 \frac{1}{p_i} .\]
Now the nature of the beast becomes a little clearer. The factors \(p\) and \(\log (1/p)\) pull in opposite directions. If you make \(p\) larger, you make \(\log (1/p)\) smaller, and vice versa. At both extremes of the allowed range, near \(p = 0\) and \(p = 1\), the value of \(p \log (1/p)\) approaches 0. In between these limits, \(p \log (1/p)\) is always positive, and should have a maximum for some value of \(p\). Figure 23 shows that this is true. It’s no coincidence that the curve has the same form as one of those in Figure 22. (If you’re curious about the location of the peak, I’ll give you a hint: It lies where \(p\) is equal to the reciprocal of a famous number.)
We can now bring in some of the particulars of the Wordle problem. The probability \(p_i\) is in fact the probability that the target word is found in Zip code \(i\).
\[H = \sum_{i} \frac{n_i}{m} \log_2 \frac{m}{n_i} .\]
And now for the final transformation. The laws of logarithms state that \(\log x/y\) is equal to \(\log x - \log y\), so we can rewrite the Shannon equation as
\[H = \sum_{i} \frac{n_i}{m} (\log_2 m - \log_2 n_i) .\]
In this form the equation is easy to relate to the problem of solving a Wordle puzzle. The quantity \(\log_2 m\) is the total amount of information (measured in bits) that we need to acquire in order to identify the target word; \(\log_2 n_i\) is the amount of information we will still need to ferret out if Zip code \(i\) turns out the hold the target word. The difference of these two quantities is what we gain if the target is in Zip code \(i\). The coefficient \(n_i / m\) is the probability of this event.
One further emendation is needed. The logarithm function is undefined at 0, as \(\log x\) diverges toward negative infinity as \(x\) approaches 0 from above. Thus we have to exclude from the summation all terms with \(n_i = 0\). We can also fill in the limits of the index \(i\).
\[H = \sum_{\substack{i = 1\\n_i \ne 0}}^{242} \frac{n_i}{m} (\log_2 m - \log_2 n_i) \]
Shannon’s discussion of the entropy equation is oddly diffident. He introduces it by listing a few assumptions that the \(H\) function should satisfy, and then asserting as a theorem that \(H = -\Sigma p \log p\) is the only equation meeting these requirements. In an appendix to the 1948 paper he proves the theorem. But he also goes on to write, “This theorem, and the assumptions required for its proof, are in no way necessary for the present theory [i.e., information theory]. It is given chiefly to lend a certain plausibility to some of our later definitions.” I’m not sure what to make of Shannon’s cavalier dismissal of his own theorem, but in the case of Wordle analysis he seems to be right. Other measures of dispersion work just as well as the entropy function.