Reviewing this month’s batch of incoming junk mail, I stumbled upon the following message:
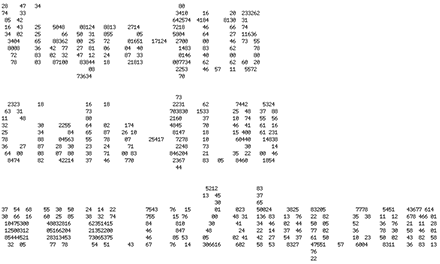
In case that image is too tiny to read, here is the first word in source-code form:
28 47 34
74 33
85 42
16 43 25 5048 08124 8813 2714
34 02 25 66 50 31 855 05
3404 65 88362 00 25 72 01651
8008 36 42 77 27 81 06 04 40
72 83 02 32 47 12 24 87 33
78 03 87100 83844 18 21813
08
73634
The basic technique is anything but novel. I can remember green-and-white-striped printouts that had my name emblazoned in the same kind of two-inch-high characters. But why are the characters here formed entirely out of numbers, rather than other ASCII glyphs? And do the numbers themselves mean anything?
I think I know the answer to the first question: The spammer thought a message composed of nothing but numerals might slip through the spam filters. (In my case, at least, it didn’t work. I fished this message out of the garbage pail.)
As for the second question, my immediate guess was that the digits are the output of some simple pseudo-random number generator. That would be an easy way to produce them, and it would also allow the spammer to make each individual message unique. On taking a closer look, however, I realized there was something quite nonrandom about the numbers in the message.
Here is the full list of digits. There are exactly 900 of them. Do you see what’s missing?
284734807433341016202332628542642574418481303116432550480812488 132714721846667434022566503185505580464271163634046588362002572 016511712427000046735580083642772781060440148383627872830232471 224873301464000807803871008384418218130077346262602008225346571 155727363470732323181618223162744253246331737038301533254837881 148802160371074555632302255640217448457046416116253484658726108 147181540061231788804563557807254177278106044014838362787283023 247122487330146400080780387100838462042135220046847482422143746 770236783058460185444521283134537306537546855305024142275437615 010235002438258320577785451436776143066166025853832747551576004 831136831376228235381112678466011047530048032816623514158481030 413446024450055236762111281250031205166204213522004684748242214 374677023678305846018544452128313453730653754685530502414227543 761501023500243825832057778545143677614306616602585383274755157 600483113683137622
There’s nary a 9 in the bunch. And in other respects too the digit distribution looks slightly off-kilter:
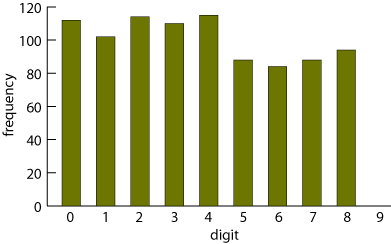
When I tabulated all the correlations between successive digits, that too looked a little fishy, although the sample is too small for any reliable conclusions.
s e c o n d
0 1 2 3 4 5 6 7 8 9
0 23 12 20 9 17 9 7 7 8 0
1 11 13 11 12 16 8 13 5 10 0
f 2 11 11 13 15 14 15 6 14 9 0
i 3 18 13 15 7 11 8 13 13 12 0
r 4 8 9 12 13 12 10 22 11 18 0
s 5 11 7 5 14 12 14 4 10 11 0
t 6 12 10 15 6 8 7 10 10 6 0
7 6 10 9 10 12 7 9 11 14 0
8 12 14 8 24 13 10 0 7 6 0
9 0 0 0 0 0 0 0 0 0 0
So what’s going on here? I think the pseudo-random generator is still a leading candidate, though it would have to be a badly implemented RNG. The absence of 9s isn’t hard to explain: We only have to suppose that the spammer was working in C and wrote the plausible-looking expression random(9), thinking that would generate integers between 0 and 9.
On the other hand, maybe it isn’t random. Maybe there’s a secret message-within-the-message. Anybody see a pattern?
While I’m talking spam, I’ll update my ongoing tally of my inbox contents. I can report that September was a good, strong month for spam, with further steady growth continuing the summer-long trend. The stock market is in retreat and credit is tight, but the purveyors of replica watches are undeterred. My receipts have crossed the 5,000-per-month threshold for the first time:
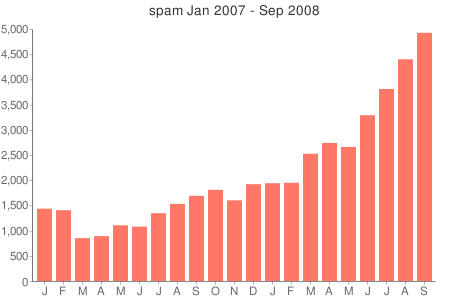
And another threshold has also been left behind: For the first time this month, more than half of my spam is written in Russian. (Based on character-set declarations, 2,858 messages out of 5,021 were in Cyrllic scripts, or about 57 percent.)
Update 2008-10-12: In response to a request in the comments, I’ve uploaded the full text (including headers) of the original email. The file is here. Incidentally, I’ve searched my spam archive for other messages like this one, without success. That in itself makes this a peculiar spam. Usually, if I get a spam once, I see dozens of copies or variants within a few days.

Well, I see a pattern, but I don’t know what it means.
Every now and then, you see that the same digit repeats consecutively three times. The first occurrence is 333 after the ten first digits. This “phenomena” occurs roughly every 64 digits:
2847348074
3334101620233262854264257441848130311643255048081248813271472184
6667434022566503185505580464271163634046588362002572016511712427
000046735580083642772781060440148383627872830232471224873301464
0008078038710083844182181300773462626020082253465711557273634707
32323181618223162744253246331737038301533254837881148802160371074
5556323022556402174484570464161162534846587261081471815400612317
888045635578072541772781060440148383627872830232471224873301464
00080780387100838462042135220046847482422143746770236783058460185
4445212831345373065375468553050241422754376150102350024382583205
7778545143677614306616602585383274755157600483113683137622823538
1112678466011047530048032816623514158481030413446024450055236762
1112812500312051662042135220046847482422143746770236783058460185
4445212831345373065375468553050241422754376150102350024382583205
7778545143677614306616602585383274755157600483113683137622
Maybe this is the spam version of a numbers station (http://en.wikipedia.org/wiki/Numbers_station), a way for spy agencies to send coded messages out to the field. Spam, like shortwave signals, is part of the ether and can be received anonymously. As an added bonus, the spy agency could raise funds by selling pharmaceuticals to silly people!
Here is a plot of the ordered pairs. The x axis is the index and the y axis is the pair. Some patterns are evident. I can’t imagine that they are an artifact of the rng, but its possible.
http://www.cs.indiana.edu/~bscastle/t2.pdf
One particular pattern
http://www.cs.indiana.edu/~bscastle/t2-zoom.pdf
This zoom highlighted a huge copied section. Maybe it was an rng + copy & paste!
284734807433341016202332628542642574418481303116432550480812488
132714721846667434022566503185505580464271163634046588362002572
016511712427000046735580083642772781060440148383627872830232471
224873301464000807803871008384418218130077346262602008225346571
155727363470732323181618223162744253246331737038301533254837881
148802160371074555632302255640217448457046416116253484658726108
147181540061231788804563557807254177278106044014838362787283023
2471224873301464000807803871008384
620421352200468474824221437467702367830584601854445212831345373
065375468553050241422754376150102350024382583205777854514367761
4306616602585383274755157600483113683137622
823538111267846601104753004803281662351415848103041344602445005
523676211128125003120516
620421352200468474824221437467702367830584601854445212831345373
065375468553050241422754376150102350024382583205777854514367761
4306616602585383274755157600483113683137622
how could I miss the copy&paste?
hmm, another pattern - look for example at the beginning of the following two lines
5556323022556402174484570464161162534846587261081471815400612317
888045635578072541772781060440148383627872830232471224873301464
note that many times, to go from a digit in the first line (x), to the digit right below it (y) you would do y=(x+3) mod 9 (remember that 9 is not playing). For example 5->8, 6->0, 2->5 and so on.
If that’s an RNG, it’s broken :)
Check out FIGlet if you are nostalgic for ASCII art. It’s free, there are lots of fonts (though not a randomish-number one), and it even does Unicode.
I’m not sure why you think the histogram that you’ve plotted looks “off-kilter”. It looks entirely typical of 900 uniform draws from the integers 0 to 8. Remember the error bars are going to be roughly sqrt(size of bar).
@ rouli and Brent Castle: Truly bizarre! I certainly didn’t see those patterns, I didn’t expect them, and I have no idea what (if anything) they might mean.
@ Iain: What caught my eye was not the variance in the digit counts as the suggestion of a systematic bias in favor of smaller numbers, or against larger ones. But you’re right. The null hypothesis is certainly not excluded.
This reminds me of the Arizona Lottery’s “Pick 3″ incident in 1998. In the Pick 3 game, players select a number from 000 to 999. But a programming error made it impossible for the digit 9 ever to be part of a winning number. See, for example, “The Case of the Missing Lottery Number” by Bill Kaigh in the January 2001 issue of the College Mathematics Journal.
Since the digit 9 is not being used, maybe this is actually some number in base 9. Perhaps if you convert it to base 10 you’ll recognize it as the expansion of pi or square root 2 or some other well-known number.
In the Pick 3 incident about 27% of the numbers had no chance of winning. I guess you couldn’t make money by buying all of the remaining numbers, but it sure would improve your odds!
http://www.jstor.org/sici?sici=0746-8342(200101)32:1%3C15:TCOTML%3E2.0.CO;2-J
@Gerry: Interpreted as a base-9 integer and converted to base-10:
21557800711710455255538736971189067184979311434258865
78308480799809889243093913713456201939041957299038496
92522829906262673817030272601845718722434818441532642
01186145590928387458644335520433398067558904370544869
11763390110513489405480553393465278460216602842071182
94392819007365124083927531356467573730341367712464596
73578972318488741099211613469405646022394034975370695
44070083245988659360516848783052576414226520984015498
00910118635540135328878932494424012743673769177999175
93166457665919619691025965877917697701459299617821176
22721203343916785719267300656350767183003001234021350
68030470193474610044996388880003812710061908728188339
09815344925956620857123514756375124734531814289772807
43939311204666991296542066037159080414685309686457513
27221078741358518055477983355859939062169804166807729
47288413808548687516349613282353013379229827161902064
95365179005
I’m not seeing pi or root 2, but who knows?
and of course, even in base 9, pi should not have a repeated pattern within it.
Let the n’th digit be d(n).
If you’ll do an histogram of d(n)-d(n-64) (mod 9) you’ll find that 3 is by far the most probable outcome, and there are no occurrences of 7 or 8 (if I recall correctly).
Any chance of uploading the original spam mail?