I’ve received the following note from Barry Cipra, bit-player’s Bureau Chief in Northfield, Minnesota, (where all hail broke loose yesterday):
Your latest postings [here and here] have motivated me to idle away some time with a variant of the problem(s) you discussed. To wit, I got to wondering what happens if you restrict yourself to taking sums of distinct pairs and positive differences of numbers from a (finite) set S — i.e., x+y and x–y with x > y in S.
It was easy, after a while, to see that the sum set is usually larger than the difference set. In particular, for the set {0, 1, 2, …, m}, the sum set is {1, 2, …, 2m–1}, while the difference set is {1, 2, …, m–1}. It seems, or at least seemed, obvious that the sum set is never smaller than the difference set, but a proof keeps slipping through my (fumbling) fingers, which suggests that either it isn’t true, or the proof is complicated, or the slow decline of my mathematical abilities has steepened and accelerated. Intuitively, each duplicate sum is associated with two duplicate differences: If a+d = b+c with a < b < c < d, then d–b = c–a and d–c = b–a. The problem, of course, is that you can have duplicate duplicates.
It seemed worth looking at how the sum/difference ratio tends toward 2 as one “grows” a set S by randomly adding numbers between 1 and some large upper bound, say m = 10,000. I wrote, ran, debugged, ran, debugged,…., and finally ran successfully a little (Basic) program to do this, and tried it with various values of m, printing out the ratio as each new (random) element got added. The number of elements required to reach any given ratio r (less than 2) seems to be proportional to sqrt(m). In particular, the number of elements to reach r=1.5 seems to be 2*sqrt(m). It would be most gratifying if this turned out to be asymptotically exact.
Barry also points out a connection with the birthday “paradox.” Here on Earth, any gathering of 23 or more people has a better-than-even chance of including at least two people with the same birthday. On Mars, where the year has 687 days, you need to assemble 32 people to have a fifty-fifty chance of such a coincidence. On Saturn, where people can have any of 1,055 birthdays, the minimum size of the group is 39. (I would add that on Pluto, with a year of 14,158 Plutonian days, the minimum likely size for a double-birthday party is 141 people. However, there can’t be that many people on Pluto, since it’s only a dwarf planet.) Anyway, the point of all this is that the number of people needed for a birthday coincidence grows in proportion to the square root of the number of possible birthdays. The calculation is similar when it comes to the number of elements in a set drawn at random from {0, 1, 2, …, m}, except that the probability we’re interested in is not that of finding two identical elements but rather that of having two pairs of elements with the same sum or difference.
Barry’s version of the problem has a satisfying symmetry. For both sums and differences, we’re looking at the upper triangle of a matrix, excluding the diagonal and everything below it. If there are no duplicates, or coincidences, then the sum set and the difference set are necessarily of the same size.
Inspired by Barry’s example, I have idled away a few of my own declining hours, and gone off on a bit of a tangent.
In an arbitrary finite set of non-negative integers, suppose there are n elements, and the largest element is m. If m is much larger than n, coincidences are unlikely among both the sums and the differences; in the limiting case, they have probability zero. If m = n–1, then the set must be the arithmetic progression {0, 1, 2, …, m}, and the number of coincidences is maximized. Barry’s algorithm for adding randomly chosen numbers to a set, one at a time, can be viewed as a way of exploring the transition between these two extremes. We can ask, at each stage of the process: What is the probability that a randomly chosen number, distinct from all the existing elements of the set, can be adjoined to the set without generating a coincidence?
Here is a somewhat different question. Instead of choosing numbers at random to add to the set, suppose we always insert the smallest number that can be adjoined to the set without creating a coincidence. In other words, we build the set from the bottom up. What does the resulting set look like?
First consider just the constraints imposed by the sum set, ignoring coincidences among differences. Starting from the empty set {}, we can obviously go on to {0} and then to {0, 1}. Next we can insert 2, because the three sums 0+1 = 1, 0+2 = 2 and 1+2 = 3 are all distinct. But we cannot add 3 to the set, because that would introduce the coincidence 0+3 = 1+2. The next permissible element is 4; the set {0, 1, 2, 4} produces the sum set {1, 2, 3, 4, 5, 6} without coincidences. Going on from there, both 5 and 6 are excluded, but 7 is okay. Working with pencil and paper, I extended this set as far as {0, 1, 2, 4, 7, 12, 20, 29}. This gave me enough to go consult the Oracle of AT&T. I found the sequence listed as No. A010067 in Neil Sloane’s Encyclopedia of Integer Sequences. The sequence is described as follows: “A B2 sequence: a(n) = least value such that sequence increases and pairwise sums of distinct elements are all distinct.” This was just what I had been looking for, and the success boosted my confidence that at least I had done the arithmetic right.
Now I tried the same method with the differences. Again the first few sets that yield no coincidences are {}, {0} and {0, 1}, but in the subtractive case {0, 1, 2} fails, because 2–1 = 1–0. On the other hand, {0, 1, 3} is without conflicts. The series continues {0, 1, 3, 7, 12, 20, 30}. It was time to visit the Oracle again. This sequence is No. A025582, but the identifying tag line is not quite what I was expecting: “A B2 sequence: a(n) = least value such that sequence increases and pairwise sums of elements are all distinct.” I had generated the series by looking at differences of distinct elements, but it turns out that sums of not-necessarily-distinct elements yield the same series. Curious.
Let’s consider the element-by-element differences between these two sequences, which I’m going to call S(n) for the sums of distinct pairs and D(n) for the differences of distinct pairs:
n D(n) S(n) D(n)-S(n) 0 0 0 0 1 1 1 0 2 3 2 1 3 7 4 3 4 12 7 5 5 20 12 8 6 30 20 10 7 44 29 15 8 65 38 27 9 80 52 28 10 96 73 23 11 122 94 28 12 147 127 20 13 181 151 30 14 203 181 22 15 251 211 40 16 289 257 32 17 360 315 45 18 400 373 27 19 474 412 62 20 564 475 89
From the first few entries in this table one might well guess that the sums will always be lagging behind the differences, so that the D(n) – S(n) sequence grows monotonically. But then there’s a reversal at n = 10, and after that it’s not clear exactly what the trend will be. The obvious question is: Can S(n) ever be greater than D(n)? This time the Oracle can’t help us; a Sequence Server search for {0, 0, 1, 3, 5, 8, 10, 15, 27, 28} comes up empty.
I tried producing a few more terms of S(n) and D(n) and their differences. Struggling with a grotesquely inefficient program, I invested an hour of cpu time, which got me as far as n = 60:
n D(n) S(n) D(n)-S(n) 0 0 0 0 1 1 1 0 2 3 2 1 3 7 4 3 4 12 7 5 5 20 12 8 6 30 20 10 7 44 29 15 8 65 38 27 9 80 52 28 10 96 73 23 11 122 94 28 12 147 127 20 13 181 151 30 14 203 181 22 15 251 211 40 16 289 257 32 17 360 315 45 18 400 373 27 19 474 412 62 20 564 475 89 21 592 530 62 22 661 545 116 23 774 607 167 24 821 716 105 25 915 797 118 26 969 861 108 27 1015 964 51 28 1158 1059 99 29 1311 1160 151 30 1394 1306 88 31 1522 1385 137 32 1571 1434 137 33 1820 1555 265 34 1895 1721 174 35 2028 1833 195 36 2253 1933 320 37 2378 2057 321 38 2509 2260 249 39 2779 2496 283 40 2924 2698 226 41 3154 2873 281 42 3353 3060 293 43 3590 3196 394 44 3796 3331 465 45 3997 3628 369 46 4296 3711 585 47 4432 3867 565 48 4778 4139 639 49 4850 4446 404 50 5122 4639 483 51 5242 5021 221 52 5297 5064 233 53 5750 5322 428 54 5997 5613 384 55 6373 6003 370 56 6800 6273 527 57 6924 6493 431 58 7459 6641 818 59 7546 6979 567 60 7788 7275 513
Would you care to place a bet on the further behavior of this series? At n = 60, D(n) – S(n) looks like it’s still growing, on the average, but it’s also still fluctuating. Will any of the dips in the curve ever plunge deep enough to bring the balance below zero? Or will the overall upward trend prevail in the long run? Maybe it’s like π(x) – Li(x) in number theory. This function—the difference between the actual number of primes up to x and an estimate proposed by C. F. Gauss—is negative for all values of x anyone has ever calculated explicitly. Nevertheless, there’s a proof that π(x) – Li(x) does eventually become positive; indeed, it changes sign infinitely often. But the first such zero crossing is somewhere out in the remotest exurbs of the number line.
I debated: Is it worth the bother of writing a better program to add a few more lines to the table? If D(n) – S(n) is positive for all values of n up to n = 60, what is the probability of discovering a negative value at n = 61, or even n = 600? I have no idea how to answer that question mathematically, but psychologically the prospects seemed pretty dim. Nevertheless, I wrote the program. Here are the next four entries in the table:
n D(n) S(n) D(n)-S(n) 61 8219 7587 632 62 8502 8017 485 63 8729 8373 356 64 8941 9071 -130
There it is: S(64) is greater than D(64). And I soon learned that this excursion into negative territory is not a one-of-a-kind freak occurrence. In the interval between n = 0 and n = 500, D(n) – S(n) is positive for 301 values, negative for 198 values and 0 for 2 values. It seems a reasonable conjecture that positive and negative values occur equally often. Here’s a graph of D(n) – S(n) for n = 0 to n = 250:
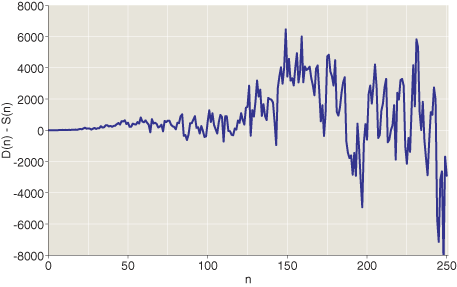
Final note: Although I have just today blundered down this interesting path, I am assuredly not the first to pass this way. I gather that I need to do some reading on Sidon sequences. Are there also connections with Golomb rulers?

” …I had generated the series by looking at differences of distinct elements, but it turns out that sums of not-necessarily-distinct elements yield the same series. Curious.”
You say curious, I say obvious. If a-b=c-d, then a+d=b+c. Either all four are distinct, or else two are equal, say a=d.
My own decline is apparent in the assertion that {1,2,…,m-1} is the difference set for {0,1,2,…,m}. I meant {1,2,…,m}.
As one randomly “grows” a set S from among the numbers 0 to m, the number of duplicates, either sum or difference, with each new number goes from none to all — that is, when you add the n+1st number, you (usually) get no duplicates when n is small (compared to m) and nothing but duplicates when n is large. In general you get some fraction, k/n. I wonder what the transition looks like.