“The fine art of turning literature into drivel” is a specialty of mine. I’ve been doing it for 30 years. Here is a specimen of drivel that I extracted from Walter Benjamin’s 1936 essay “The Work of Art in the Age of Mechanical Reproduction”:
Artistic receptivity which, by means of gas masks, terrifying megaphones, flame throwers, and beaches which face the public present conditions. The camera, with a theology of art. We do not deny that individual reactionary manner by the unarmed eye. A bird’s-eye view best captured by a clock.
If the rhetoric of megaphones and flame throwers is too strident for your taste, try some Edgar Allan Poe, made even more breathless than usual by the algorithmic mixmaster:
And the faintly rappiness of the accompare, name a tappiness: his holier odorous and unwonted heart a spirits hallowed fast all! While even in the Naiad from its purple curtain rustle throbbing bride In her brow What wild weird clime that her head, Repenting from the headlong– Her world of moan
Maybe you can guess whose n-grams these are:
These frequencies of memory. The programmer for banana phenomenon. Am I the original text, but writing familiarity. It is nonsense, but nevertheless it shows only those days, so I had to the rhetoric of megaphones, flame them down one another corresponding on typewriters. In second-order drivel.
Yes: That’s a self-referential pastiche of the very document you are reading at this moment. And don’t bother telling me that the scrambled version is more fun than the original; I already know that.
I’m going to say a bit more about the algorithms behind this silliness, but first I invite you to go make your own drivel. The program that generates this mish-mash runs as a web app. You can mangle a few cultural treasures that I’ve looted from Project Gutenberg and elsewhere. And you may also be able to drivelize texts of your own choosing. (For this you’ll need an up-to-date web browser.) Have fun, but come back when you’re done.
So how do we transform literature into drivel? The simplest strategy is just to choose letters randomly and independently from the source text and write them down one after the other. Call this zeroth-order drivel:
,ca adigaigjr nre hs n eveel’adnwbtfs s!notm samhhd cdseghs xhi annm no,eghkg ne ttidpatlgtrirTefgsuw g ehilehn:tosiceerlI”u loaotiiuom aou
The source text in this case is Alexander Pushkin’s novel-in-verse Eugene Onegin (in an English translation by Charles H. Johnson). The drivel mimics the letter frequencies of the original—lots of e’s and t’s, fewer f’s and v’s—but captures no information at all about the sequence in which the symbols appear in the original.
After zeroth-order drivel comes first-order drivel, which takes each character of the source text and tallies the frequencies of all the symbols that might possibly follow it. These frequencies yield a table of probabilities for the next drivel character. Suppose at some point in the driveling process we have just generated a v. Then we must find out what characters follow v in the source text, and how often each of them appears. It turns out there are 1,415 v’s in the Onegin text, and they are followed by 15 different characters:
pair count proportion
ve 974 0.6883
vi 193 0.1364
va 102 0.0721
vo 72 0.0509
vg 24 0.0170
v 11 0.0078
v, 10 0.0071
vy 8 0.0057
vs 5 0.0035
vu 4 0.0028
v' 3 0.0021
vn 3 0.0021
vé 3 0.0021
v; 2 0.0014
vá 1 0.0007
Thus the next character of the drivel stream will be an e with probability 0.69, an i with probability 0.14, and so on. Whichever symbol is chosen from this list will become the seed for the next pass through the first-order driveling process. If it’s an a, for example, then in the next round the algorithm will look at all the characters that can follow a (there are 35 of them), and make a choice according to the relative frequencies.
First-order drivel is a huge improvement over the zeroth-order stuff, but nevertheless it shows only the vaguest glimmers of linguistic structure:
andilielderonlyo oouadion t, honin Itheatishend aricivee d porg ad eandd t this. ad k: withiofou hene tone Gontrs ted)— ct), he touthet t h, te g owsin d.
Common digraphs such as th have begun to show up, and every now and then we get a fully formed word, such as this. But for the most part it’s still monkeys pounding on typewriters.
In second-order drivel, symbols are taken two at a time, and probabilities are calculated for all possible successors to each pair. The result is something you could almost read aloud (perhaps with a Scots accent):
The of hise fing flink waime ing, My rectearks the gold thaught worns haverne’s peave st ands he bre drink alloveremid, ane why ned, heady; ifer grens, evill
With third-order drivel, probabilities are calculated from triples of letters:
We meetness pressons, and of his longuisencess he giddles, bence wing; Tatyana ladiesteps, the pain in to the servings, or sere nevent I catch oth
Here we enjoy brief moments of seeming lucidity, as letters condense into words, and sometimes the words organize themselves into phrases—but then the protodiscourse dissolves back into longuisencess again.
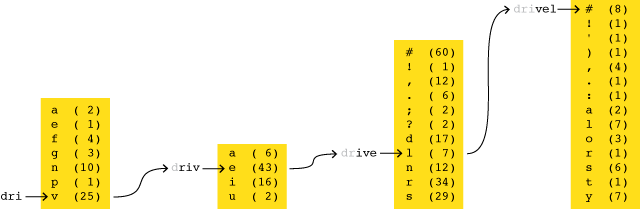
How to turn literature into drivel: The four panels show the third-order drivel algorithm in action with letter frequencies derived from Pushkin’s Eugene Onegin. The initial seed (far left) is the three-letter sequence dri. Out of the seven characters that are observed to follow dri in the Pushkin text—shown with their frequencies in parentheses—the algorithm makes a weighted random choice, which in this case is the letter v. In the next round, the seed sequence is riv, and the chosen letter is e. Then the pattern ive leads to selection of an l, and finally vel is followed by a word space (denoted #). It’s worth noting that the complete word drivel does not appear in the text of Onegin.
The drivel examples given at the beginning of this article come from higher-order drivelers, with probabilities calculated from strings of six, seven or eight characters. At this level there’s no doubt we’re in the realm of language rather than mere alphabet soup. Even though there’s no sign of grammatical structure or meaning, what comes out of the program is immediately recognizable as English. If you know what to look for, the writerly tics of individual authors begin to show through. This is what intrigued me when I first began driveling back in 1983. In a “Computer Recreations” column I wrote:
What is remarkable is that the product of this simple exercise sometimes has a haunting familiarity. It is nonsense, but not undifferentiated nonsense; rather it is Chaucerian or Shakespearian or Jamesian nonsense. Indeed, with all semantic content eliminated, stylistic mannerisms become the more conspicuous. It makes one wonder: Just how close to the surface are the qualities that define an author’s style?
The program that generated my 1983 drivel was written in Microsoft BASIC and ran on a PC with two floppy drives but no hard disk. There was no Project Gutenberg in those days, so I had to type in the texts myself. I spent a long, bleary night transcribing the “Ithaca” chapter from James Joyce’s Ulysses. (The chapter, also known as Molly Bloom’s soliloquy, is a marathon run-on sentence.) Once the keyboarding was done, the program would grind out drivel at a rate of one or two characters per minute.
The first version of the program was built around matrices of precomputed probabilities. Given an alphabet of s symbols, a first-order drivel program needs an s × s matrix, like this one for a 28-symbol alphabet:
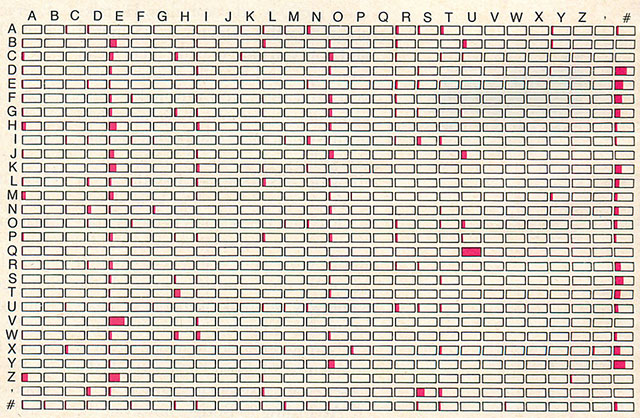
The chart is based on the third act of Hamlet. Find the row corresponding to the current symbol in the drivel process, then scan across the columns to read off the probabilities for all possible successor symbols. (The last two symbols are the apostrophe and the word space, represented as ‘#’.) Note that this is a stochastic matrix: The entries in each row sum to exactly 1.
Moving on to second-order drivel, the matrix expands to s2 rows, which accommodate all the two-symbol sequences from aa through ##, each row having s columns. In the case of a 28-symbol alphabet, that comes to about 22,000 matrix elements, which seemed like Big Data back then. The next stage, a third-order matrix, would have more than 600,000 elements, which was more than I could squeeze into 256 kilobytes of memory. The array wouldn’t even fit on disk (maximum capacity 320 kilobytes).
I gave some thought to sparse-matrix methods, but then I had a better idea.
The fact is, all the information that could be incorporated into any frequency table, however large, is present in the original text, and there it takes its most compact form…. What the frequency table records is the frequency of character sequences in the text, but those sequences, and only those sequences, are also present in the text itself in exactly the frequency recorded.
The algorithm suggested by this observation searches through the full source text to create a new, one-dimensional frequency table for each seed pattern. Instead of precomputing and storing the probabilities associated with every possible seed, we regenerate them on the fly, as needed. The saving of space comes at the expense of wasting time, since the same search is repeated for every occurrence of an n-gram pattern. Various methods of hashing, caching or memoization could have fine-tuned the tradeoff between space and time, but I didn’t know that then. A few correspondents pointed it out after the article appeared.
Several other correspondents mentioned another shortcut, which I’m going to call the Shannon algorithm. In a followup column I wrote:
Bobby Bryant, James W. Butler, Ronald E. Diel, William P. Dunlap and Jim Schirmer pointed out still another algorithm that is not only faster than the one I gave but also appreciably simpler. It eliminates frequency tables entirely. When a letter is to be selected to follow a given sequence of characters, a random position in the text is chosen as the starting point for a serial search. Instead of tabulating all instances of the sequence, however, the search stops when the first instance is found [wrapping around to the beginning if necessary], and the next character is the selected one. If the distribution of letter sequences throughout the text is reasonably uniform, the results should closely approximate those given by a frequency table.
The caveat at the end of that paragraph merits a further comment. When the distribution of sequences is not uniform, the failure can be spectacular. In HAKMEM item 176 Bill Gosper named it the banana phenomenon. Suppose you are running the Shannon algorithm on a 100,000-character text that includes a single instance of the word banana and no other instances of the trigrams ana and nan. Let the seed pattern be ana. When you start a sequential search from a random point in the string, you have 99,998 chances to come upon the first ana and only two chances to reach the second instance.
In spite of this pitfall, I have adopted the Shannon algorithm for the online drivel generator; it’s just too easy and elegant to pass up. But it can indeed wander into strange blind alleys. For a live demonstration of what can go wrong, try some third-order driveling with the file named “Hayes-banana.txt”.
Why do I call this the Shannon algorithm? Because Claude Shannon described it in 1948, in “A Mathematical Theory of Communication.” His implementation involved opening a book at a random page. He gave several examples of convincing drivel he produced by this pencil-and-paper method.
Shannon wasn’t the only predecessor. Even earlier—a full century ago—A. A. Markov wrote his paper on “An example of statistical investigation of the text Eugene Onegin concerning the connection of samples in chains.” It was a recent encounter with this paper that brought me back to driveling 30 years after my first adventure. As noted here a few weeks ago, I have recently given a talk on the early history of Markov chains. The video (FLV, MP4) and audio (MP3) are now online, and so are the slides (HTML). Finally, my latest American Scientist column is on the same theme.
There remains a personal question: Why does this kind of goofiness amuse me so? Am I the only one susceptible to its charms? Perhaps it is a vice that I should keep to myself, like an inordinate fondness for puns or limericks. But, the fact is, I glimpse something both comic and poetic in some of this drivel. The fourth-order drivel below is based on the banana file. In some sense I wrote this, and yet I can take very little credit for its imagery, its cadences, its sheer cleverness for clues, theorems and eyeglasses.
Figuring for banana or Mississississississississing for me, I have made it right, new particles, the University of sciency, but writing for its sheer clues, the University of the algorithm is widely admired for clues, theorems. As for banana or Missing link, the source of the back page of the source of the University of the University of the Holy Grail, the University of various permutations, and F’s of the Holy Grail, the University of the University of my chosen pattern word algorithm has not easy. Indeed, I spend of the University of the University of sciency, but writing for newspaper, M’s and F’s of theorems. As for newspaper, now of theorems. As for newspaper, M’s and eyeglasses. The detective search of the Northwest Passage, the Holy Grail, theorems. As for its sheer cleverness as a lot of one another, now of sciency, but writing a computer programmer for banana or Missississississississing link, the Holy Grail, theorems. As for its sheer clues, theorems. As for banana or Missississississing for bargains, the University of the University of the University of the Holy Grail, the source of the plumber for clues, the Northwest Passage, the University of the Holy Grail, theorems. As for me, I have made it right, the algorithm was invented by Robert S. Boyer and eyeglasses.