First Links in the Markov Chain:
Probability and Poetry
Brian Hayes
Harvard School of Engineering and Applied Sciences – ComputeFest – January 23, 2013


Events congruent to 13 modulo 100
What’s a Markov chain?
Classical probability theory
- Principle of independence.
- Compound probability: p and q = pq.
- Law of large numbers.
Markov probability theory
- Principle of independence.
- Compound probability: p and q = pq.
- Law of large numbers?
What’s a Markov chain?
- Set of states.
- Transitions between states.
- Future depends on the present.
- Future does not depend on the past.
Examples

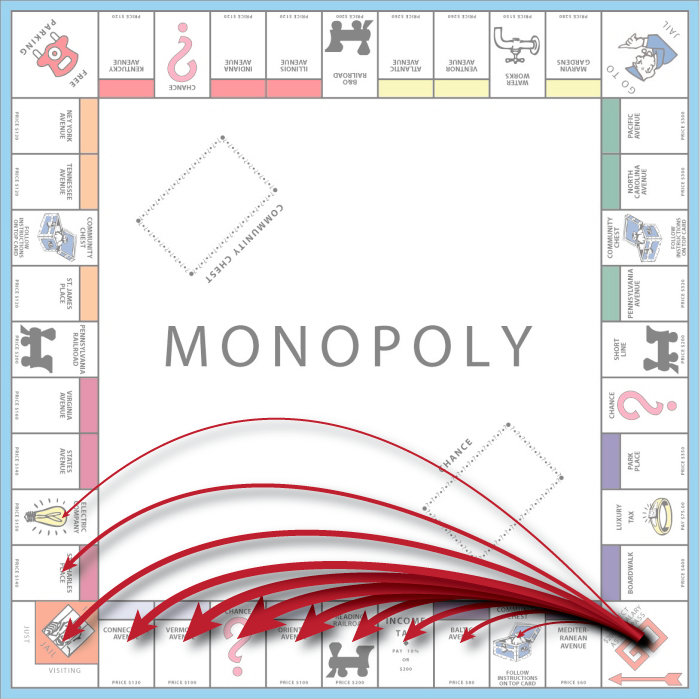

Game of Monopoly
- At least 40 states.
- At least 40 × 11 transitions between states.
- Fate depends on where you are.
- Fate does not depend on how you got there.
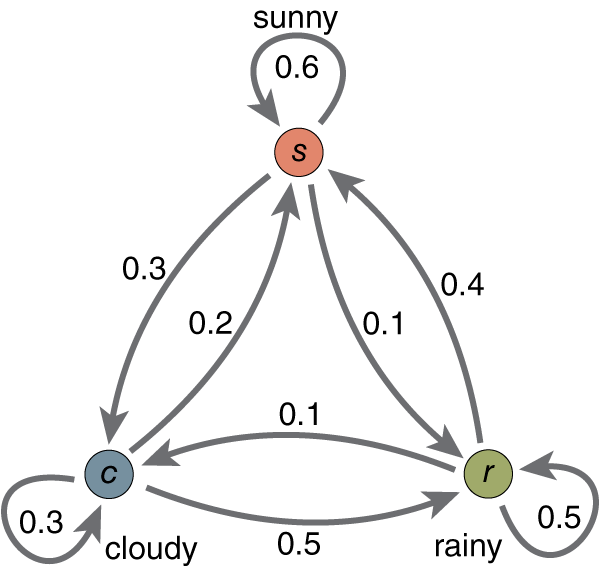
Markov model of the weather
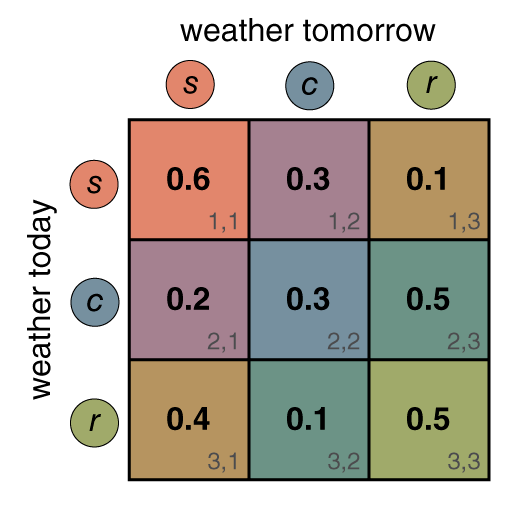
Powers of the transition matrix: 1
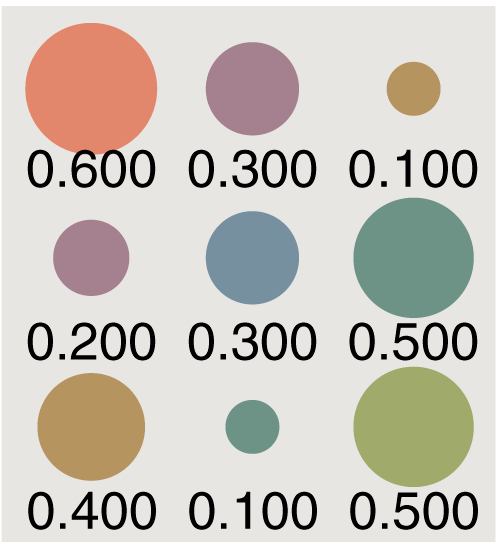
Powers of the transition matrix: 2

Powers of the transition matrix: 3
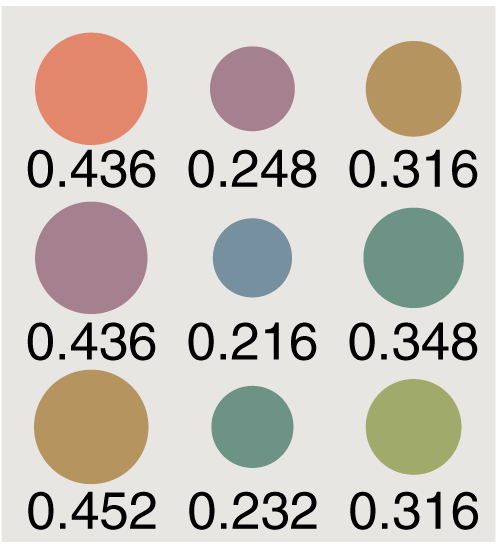
Powers of the transition matrix: 4

Powers of the transition matrix: 5

Powers of the transition matrix: 7
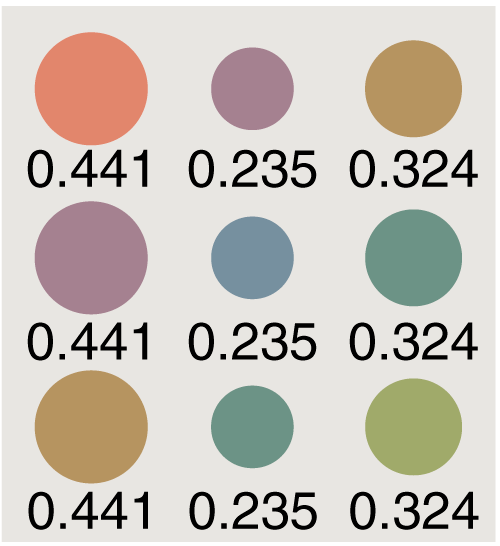
Stochastic matrices
\( 0 \le P_{i,j} \le 1 \)
\( \sum_j P_{i,j} = 1 \)
Largest eigenvalue has \( \lvert\lambda\rvert = 1 \)
If irreducible, \( \pi P = \pi \) and \( \lim_{n \to \infty} P^n = \pi \)
Classification of Markov chains
- Ergodic (aka regular or irreducible).
- Absorbing.
- Periodic.
- Finite or denumerably infinite.
- Discrete-time and continuous-time.
Larger examples
- Ising model and other spin systems.
- The Google PageRank algorithm.
- Bioinformatics.
- Speech recognition.
- Randomized algorithms.
To someone working in my part of the world, asking about applications of Markov chain Monte Carlo (MCMC) is a little like asking about applications of the quadratic formula. The results are really used in every aspect of scientific inquiry.—Persi Diaconis
History





Andrei Andreevich Markov
- 1856–1922.
- Father managed the Valvatiev estate.
- Married Maria Valvatieva.
- One son, A. A. Markov, born 1903.
Markov's Academic Career
- Student at St. Petersburg, with Chebyshev.
- Early work in number theory, continued fractions, PDEs.
- Doctorate 1884.
- U Petersburg: associate then extraordinary then ordinary professor.
- Academy of Sciences: adjunct then extraordinary then ordinary academician.
- Retirement 1905 (age 49).
Markov in Public Life
- Anti-tsarist gadfly ("Andrew the Furious").
- Excommunicated by request.
- The Maxim Gorky affair.
- 300 years of Romanovs; 200 years of Ars Conjectandi.
The Chuprov Correspondence
I note with astonishment that in the book of A. A. Chuprov, Essays on the Theory of Statistics, on page 195, P. A. Nekrasov, whose work in recent years represents an abuse of mathematics, is mentioned next to Chebyshev.—A. Markov
What led Markov to his chains?
- Logical outgrowth of work begun by Chebyshev on law of large numbers.
- Connections with Bernoulli urn problems.
- The great quarrel with Nekrasov.
The Feud
P. A. Nekrasov

At opposite poles
- St. Petersburg vs. Moscow.
- Anti-tsarist vs. monarchist.
- Secularist vs. ecclesiatic.
Nekrasov's argument for free will
- Voluntary acts are those without causal connections, like independent trials in probability theory.
- The law of large numbers applies only to independent trials.
- The law of large numbers is observed to hold in social statistics.
- Therefore people act voluntarily, with free will.
Markov's refutation
- Ignored the philosophy and theology; attacked the mathematics.
- Statements of the law of large numbers commonly assume independence, but is the assumption necessary?
- 1906: Markov finds a model in which law of large numbers holds for dependent variables.
- 1907–11: Extends the theory to broader classes of systems.
- Basic idea: Prove convergence of the transition matrix.
What happened next?
- Nobody noticed.
- (Except Nekrasov.)
- Seemed a mere technical footnote refining the conditions necessary for proving the law of large numbers.
- No hint of applications.
I am concerned only with questions of pure analysis.... I refer to the question of the applicability of probability theory with indifference.—Markov to Chuprov
Eugene Onegin
From widow Clicquot and from Moët,
the draught whose blessings are agreed,
in frosted bottle, for the poet
is brought to table at full speed.
Bubbles like Hippocrene are spraying;
once, with its foaming and its playing,
(a simile of this and that)
it held me captive; tit for tat,
friends, recollect how I surrendered
my last poor lepton for a sup!
recall, by its bewitching cup,
how many follies were engendered;
how many lines of verse, and themes
for jokes, and rows, and merry dreams!


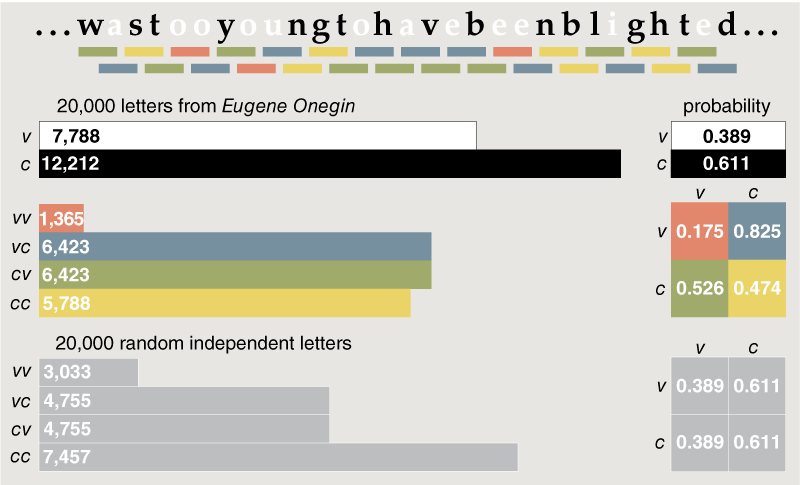
Markov's Onegin project
- First 20,000 characters (70 stanzas).
- Remove punctuation and word spaces.
- Count vowels and consonants.
- Count pairs vv, vc, cv, cc.
- Calculate moments (mean and variance).
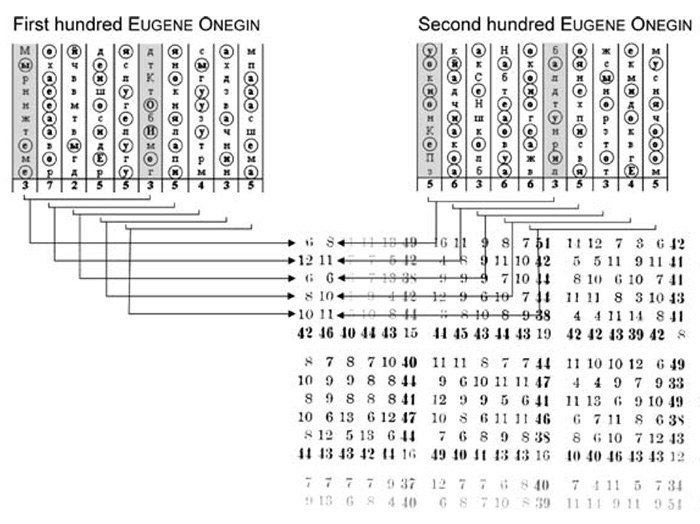

Pencil-and-paper counting

Searching for vowel pairs

Results
The Dénouement
What became of Markov chains?
- They're everywhere in the sciences.
- But Markov would hardly recognize them.
- Proving eventual convergence no longer the main point.
What became of Markov?
- On the winning side, politically, after 1917.
- But still a malcontent: bootless.
- Nekrasov sunk into obscurity.
How did these ideas reach us?
- Well known but not well read.
- Early reviews by Polya and J. M. Keynes.
- 1928 ICM meeting in Bologna.
- Claude Shannon's use of Markov chains in defining the entropy of language, 1948.
- Metropolis Monte Carlo algorithm.
Translations of the Onegin paper
- Much of Markov's work still only in Russian.
- 1955 translation by Morris Halle, but never published.
- Translation by David Link and others, published in Science in Context (2006).

How did these ideas reach me?


First-order drivel
thilare d plehenthted Theg sheso pa lyiklg utcout Scrpauscricre cobaives wingervet Ners, whe ilened te o wn taulie wom uld atimorerteansouroocono weveiknt hef ia ngry'sif farll t mmat and, tr iscond frnid riliofr th Gureckpeag cloumarospbe ish llalsme nwilais foyâ hashkesuthem, thin ar by s thets y tt the lit han oro d suplo denongl Thinwone, he wimine; eyospane
Third-order drivel
old in ene's long... whirls absorphe poor, fore just for graving, that appleasoness poet! At oness, and no fall makestic to us, infessed Russion-bently our then a man thous always, and toops in he roguestill shoed to dispric! Is Olga's up. Italked fore declaimsel the Juan's conven night toget nothem, stradition; but societ regraditiny at waken; in hearlieurse,
Fifth-order drivel
tossing the poetic she cards, and so two; there the heartache, did it face to festal cup, she truthfully inlaced. Meanwhile with jealousy bench, and so it was his time. But she trick. Let message we visits at dared here bored my sweet, who sets no inclination, and Homer, so prose, weight, my goods and envy and kin. It's obvious.
Seventh-order drivel
still deaf as howd'youdo, still has Monsieur Triquet has ceased its face, he wished me joy: lately winter's hand for the case, others who has chosen to encase herself, is Lensky, who has long would launch into self-sacrifice; all measure, Lensky, the dreams, o dreaming the hand over... How could alter or worse, flows and reverie's sacred land!
eau 2 ("Rousseau", "château")
eaut 18 ("beauty", "beauties")
eau. 1 ("Rousseau.")
eaub 1 ("Chateaubriand")
eaux 4 ("Bordeaux", "tableaux")
eau, 1 ("Rousseau,")
eau 2 ("Rousseau", "château")
eaut 18 ("beauty", "beauties")
eau. 1 ("Rousseau.")
eaub 1 ("Chateaubriand")
eaux 4 ("Bordeaux", "tableaux")
eau, 1 ("Rousseau,")
auti 2 ("beauties", "cautious")
auty 18 ("beauty")
auto 1 ("autocrat", "autograph")
auth 1 ("author")
autu 4 ("autumn")
aut. 1 ("comme il faut.")

Thanks
email: brian@bit-player.org
slides: http://bit-player.org/wp-content/extras/markov/
Harvard School of Engineering and Applied Sciences – ComputeFest – January 23, 2013