Browsing in the library stacks the other day, I came upon this passage in a 1970 paper discussing the uses of computers in mathematics:
![Lander and Parkin's counter-example [26] to Euler's conjecture in the theory of diophantine equations that no nth power equals the sum of less than n nth powers---namely, that 144^5 = 27^5 + 85^5 + 110^5 + 133^5 is highly satisfying, but does not contribute to the conceptual framework of mathematical activity.](http://bit-player.org/wp-content/uploads/2014/11/Thwaites-passage-fifth-powers-eqn.png)
Notice anything fishy about that equation? On the right side of the equal sign we have an odd number of odd numbers, and so their sum must be odd; but the power of 144 on the left side is even.
I’m not clever enough to have caught that parity violation on first glance; I noticed it only later. On the other hand, my experience as an editor has taught me never to trust an author’s arithmetic. I had a computer sitting in front of me, open to an IPython notebook, so I typed in the numbers:
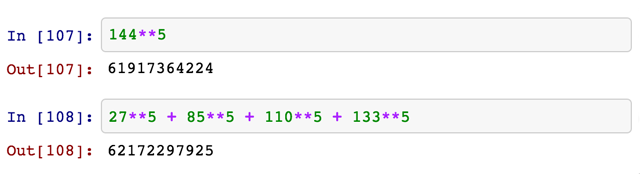
Had I just discovered that a 50-year-old counterexample to a 250-year-old conjecture is not in fact a counterexample after all? Surely not. Someone must have erred in copying the equation from the original source.
So I decided to track down that source. The reference in the quoted passage directed me to a 1966 paper by L. J. Lander and T. R. Parkin, which I quickly found online. However, the reference is mistaken; the cited paper says nothing at all about fifth powers and has no equation resembling the one above.
A faulty equation and a wayward reference within a single paragraph: That’s not so good. But I’ve done worse myself, and my purpose here is not to criticize an errant author (whom I’m not going to name). What interests me is how one might go about correcting the error in the equation and finding the true counterexample to the Euler conjecture. Here are some strategies I might have tried that morning:
- I was sitting in a university library. I had all the apparatus of scholarly research at my fingertips. I could turn to MathSciNet, say, and identify the correct paper by Lander and Parkin.
- I was sitting at a computer with a wifi connection. I had all the resources of the Internet at my fingertips. I could Google it, or consult some more specialized database such as the OEIS.
- I could just guess the answer. On the assumption that exactly one of the five terms has been altered, I would expect to come up with the correct equation after just a few tries.
- I could start from scratch. I could write a program to repeat the computer search that Lander and Parkin evidently used to discover the equation in the first place.
- I could bring the might of mathematics to bear on the problem. That is, I could try to “solve the equation.”
At this point you might want to stop reading, choose your own favorite method, and give it a try. The answer, once you have it, is not all that illuminating, but I found the process of searching had its moments of interest.
If guessing is one of your strategies, you had better try it first. I already had the equation entered into the IPython notebook, where I could easily alter a value and observe the result. (A spreadsheet would serve as well in this role.) I started with the \(27^5\) term, reducing it to \(26^5\), then \(25^5\), and so on, but the effect was too small. Even setting that term to zero or to \((-27)^5\) left an excess, so I moved on to the \(85^5\) term. Proceeding in this way, it didn’t take long to pinpoint the error.
A question I haven’t been able to answer through web search is whether the erroneous equation from that 1970 paper has propagated into the subsequent literature. I have found no evidence of it, but I have little confidence in the ability of current search technology to answer the question reliably. Gathering quantitative data—how many times does the equation appear on the web?—also seems to be out of reach.
The issue goes beyond Google and the other web search engines. MathSciNet claims to accept search strings in TeX format, but I’ve never figured out how to make it work. As for the OEIS, the search function there is specialized for finding integer sequences—as one might expect in an Online Encyclopedia of Integer Sequences. Searching for an equation is an “off label” use of the archive. Still, I was sure I’d find it. I tried searching for 61917364224 (which is \(144^5\)), and got 47 hits. (It’s a popular number because it’s a product of many small factors, \(2^{20} 3^{10}\), and is also a Fibonacci number.) However, none of those 47 sequences has anything to do with the Euler sum-of-powers conjecture or the Lander-Parkin counterexample. Yet the equation I was looking for does indeed appear in the OEIS, namely in sequence A134341.
The next approach—redoing the entire computation from scratch—turned out to be easier than I expected. Lander and Parkin ran their search on a CDC 6600, which was the most powerful computer of its time, the world’s first megaFLOPS machine, designed by Seymour Cray early in his career. I don’t know how long the computation took on the 6600, but there’s not much to it on a modern laptop. Here’s some Python code:
import itertools as it
def four_fifths(n):
"""Return smallest positive integers ((a,b,c,d),e) such that
a^5 + b^5 + c^5 + d^5 = e^5; if no such tuple exists
with e < n, return the string 'Failed'."""
fifths = [x**5 for x in range(n)]
combos = it.combinations_with_replacement(range(1,n), 4)
while True:
try:
cc = combos.next()
cc_sum = sum([fifths[i] for i in cc])
if cc_sum in fifths:
return(cc, fifths.index(cc_sum))
except StopIteration:
return('Failed')
The first step here is to precalculate the fifth powers of all integers less than a given limit, n. Then we generate all combinations of four integers in the range from 1 to n, starting with the 4-tuple (1, 1, 1, 1) and continuing to (n, n, n, n). For each combination we look up the fifth powers of the integers and check to see whether their sum is also present in the precomputed vector of fifth powers. Invoking this program as four_fifths(150) returns the correct answer in about 30 seconds. A little sad, isn’t it? This was once a research project fit for a supercomputer, and now it’s reduced to the level of a homework assignment.
The final tool we might apply to this problem is the hammer of mathematics. I would put the question as follows. We are looking for integer solutions to this equation:
\[a^5 + b^5 + c^5 + d^5 - e^5 = 0.\]
In that quest, do we gain any significant leverage by knowing that:
\[27^5 + 85^5 + 110^5 + 133^5 - 144^5 = 254933701 ?\]
Can we take the number 254933701 and apply some algebraic or analytic hocus pocus that will lead us directly to the correct values of a, b, c, d, e? If we make no further assumptions or guesses, I believe the answer must be no. After all, there are innumerable values for a, b, c, d, e that we can plug into our equation to get something other than 0. Consider this example:
\[30^5 + 69^5 + 82^5 + 86^5 - 100^5 = 43.\]
That’s a very near miss—it comes within 5 parts per billion of being a true solution—and yet it tells us nothing about the set of correct solutions except that this isn’t one of them.
An erroneous equation seems to be useful only if we know quite a lot about the nature of the errors. For example, in the faulty equation from 1970, if someone tips you off that all the terms are correct except for \(85^5\), you can form the equation
\[85^5 - x^5 = 254933701\]
and solve for \(x\). If \(x\) turns out to be an integer, you have your answer. And indeed this is the case:
\[x = \sqrt[5]{4182119424} = 84.\]
But is this procedure better than guesswork? Is it different from guesswork?
Just for the record, the correct Lander-Parkin equation is:
\[27^5 + 84^5 + 110^5 + 133^5 = 144^5 = 61917364224.\]
After discovering their counterexample to the Euler conjecture, Lander and Parkin, together with John Selfridge, made some conjectures of their own. Suppose an nth power can be partitioned into k smaller nth powers. They conjectured that k is never less than \(n-1\). And they asked whether there always exists an example where \(k = n-1\). You might try to settle the latter question for the case of \(n = 6\). Can you find a set of five 6th powers that add up to another 6th power? For this problem, Google won’t help you, because the answer is unknown. No one has even identified a set of six 6th powers that sum to a 6th power. If you approach this task as a computational challenge, it’s rather more than a homework assignment.