bit-player

A while ago I wrote about the playground ritual of choosing teams for a ball game. The simplest algorithm has two captains, A and B, who take turns choosing players until everyone is assigned to one team or the other. Call this the ABAB algorithm. Donald B. Aulenbach suggested a very easy modification that produces more closely matched teams. Aulenbach’s proposal is the ABBA algorithm, where A gets the first pick in the first round but B goes first in the second round, and they continue alternating in successive rounds. (Another way of describing the same process is that A begins with a single turn and thereafter both captains take two turns in a row.)

For a quantitative model of this process, let’s suppose each player’s ability is represented by an integer chosen uniformly at random from the interval 1 through m. We’ll let the total number of players, n, always be even, so that the two teams will be of the same size. After we have divvied up all the players, we sum the strengths of the two teams and calculate the discrepancy—the absolute value of the difference. Stephan Mertens of the the Otto von Guericke Universität in Magdeburg (who put me onto this problem in the first place) has shown that the expected discrepancy for the ABAB algorithm is m/2 × (n–1)/n; thus as n becomes large the discrepancy approaches m/2.

What about the ABBA algorithm? Here are some numerical results:

                         discrepancy

  n        m       ABAB     ABBA     exact

  4        4        1.4      0.7       0.7
  6        8        3.4      1.4       0.9
  8       16        7.0      2.3       1.2
 10       32       14.7      4.2       1.7
 12       64       29.2      7.2       2.3
 14      128       59.5     13.7       3.6
 16      256      122.4     23.9       5.7
 18      512      244.6     47.6       8.4
 20     1024      490.6     90.6      14.2
 22     2048      970.4    168.9          
 24     4096     1944.9    315.7          
 26     8192     3972.5    621.5          
 28    16384     7907.9   1177.9          
 30    32768    15892.6   2291.4
 32    65536    31877.2   4520.0          

For each line of this table I ran the ABAB and ABBA algorithms on 1,000 randomly generated sets of numbers with the indicated values of n and m, then averaged the results. Up to n=20 I also found the optimum partitioning of each set, by a brute-force enumeration. The values of m are chosen so that log₂m = n/2. Most sets with these values of m and n have many perfect partitions, with discrepancy zero—but of course neither the ABAB nor the ABBA algorithm is guaranteed to find these ideal solutions.

Here are the same data in graphic form:

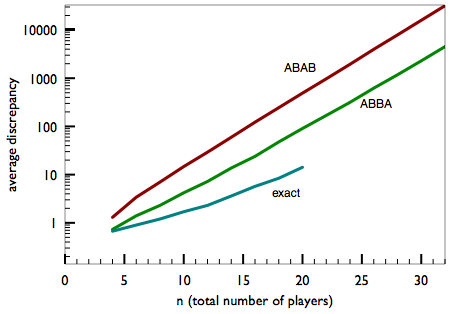
Clearly, ABBA is superior to ABAB, just as one might expect.

Questions:

1. What is the expected discrepancy of the ABBA algorithm, as a function of n and m?
2. Is ABBA the optimal algorithm of its type? Of course it is not the best of all algorithms; brute-force enumeration is better, at the cost of exponential computing time. There are also superior heuristics, but they cannot be implemented with a fixed sequence of choices, determined in advance. ABBA is a “blind” algorithm: It applies the same sequence of operations to all sets of data. Is there any other blind algorithm that outperforms it?
3. The uniform random distribution of abilities is probably not very realistic; a normal distribution would be more plausible. Would this make any difference in the performance of the algorithms?
4. Surely someone has worked on this problem before?

Going back to my own childhood, I don’t think the kids in my neighborhood ever discovered the ABBA algorithm. We did recognize the inherent advantage of choosing first, and we compensated by adopting a separate ritual to decide who got the first pick. In baseball, this involved a hand-over-hand struggle for a grip on the bat. Sometimes I think the preliminaries were more fun than the game.