For the past few weeks the Sunday New York Times has been publishing a puzzle called Capsules, devised by Wei-Hwa Huang. Here are the instructions:
Place numbers in the grid so that each outlined region contains the numbers 1 to n, where n is the number of squares in the region. The same number can never touch itself, not even diagonally.
Here is a partially completed example:
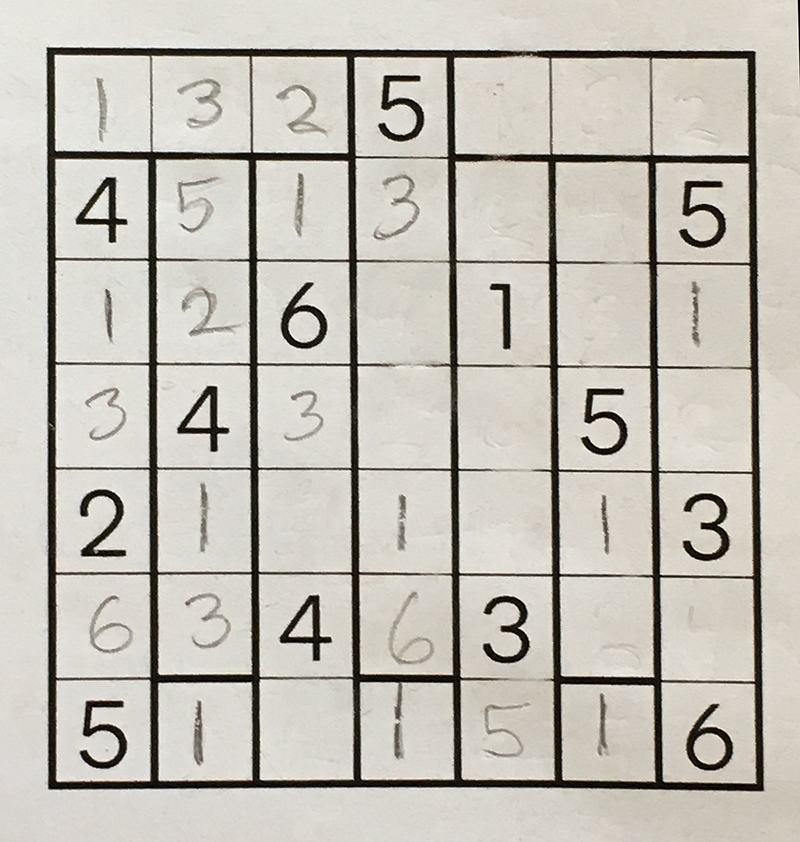
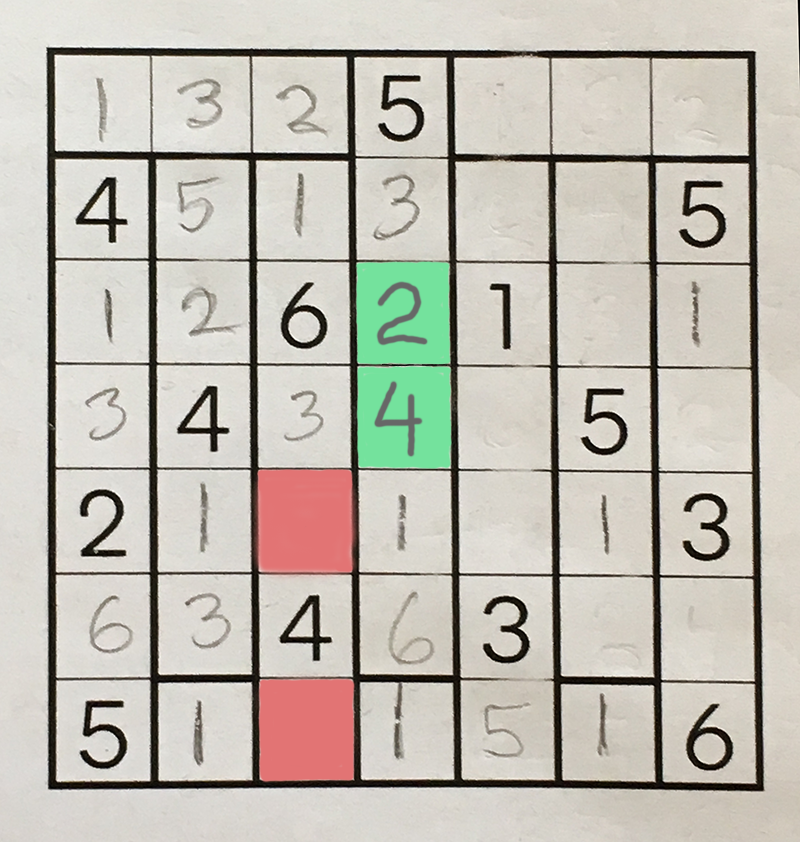
The black, pre-printed numbers are the “givens,” supplied by the puzzle creator. I filled in the pencil-written numbers in a sequence of “forced” moves dictated by two simple rules:
- A number can be placed in a square if no other number is allowed there. For example, the three singleton squares in the bottom row must each hold a 1, and these squares are the obvious place to start solving the puzzle. After the 1s are written in, the square outlined in yellow in the diagram below can also be filled in; its neighbors forbid any number other than 3.
- A number can be placed in a square if the number has no other possible home within a region. The blue-outlined 1 in the diagram below was determined by this rule. There must be a 1 somewhere in the region, but none of the other squares can accommodate it.
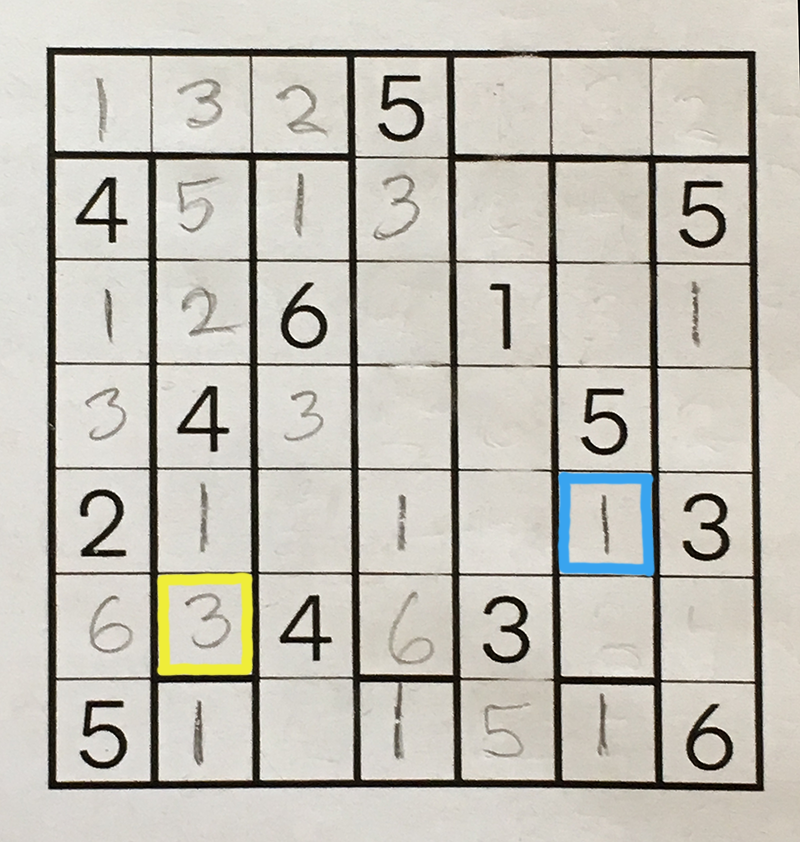
At this point in the solution process, with the grid in the state shown above, I was unable to find any other blank squares whose contents could be decided by following these two rules and no others. But I did spot a move based on a different kind of reasoning. Consider the two pairs of open squares marked in color:
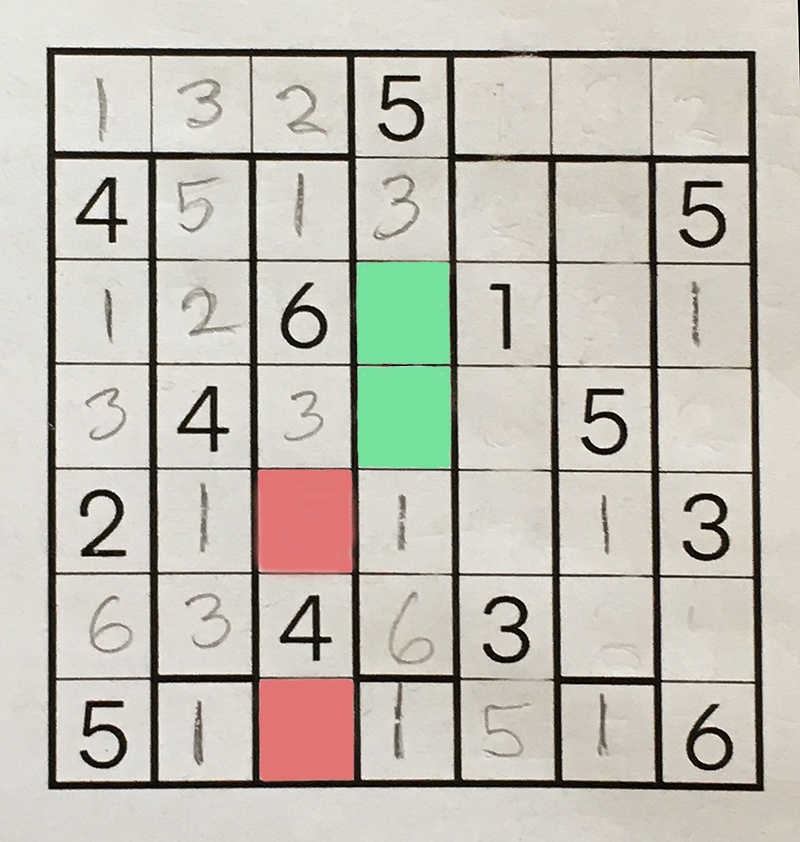
The salmon-pink squares must hold the numbers 2 and 5, but it’s not immediately clear which number goes in which square. Likewise the lime-green squares must hold 2 and 4, in one order or the other. I submit that the numbers must have the following arrangement:
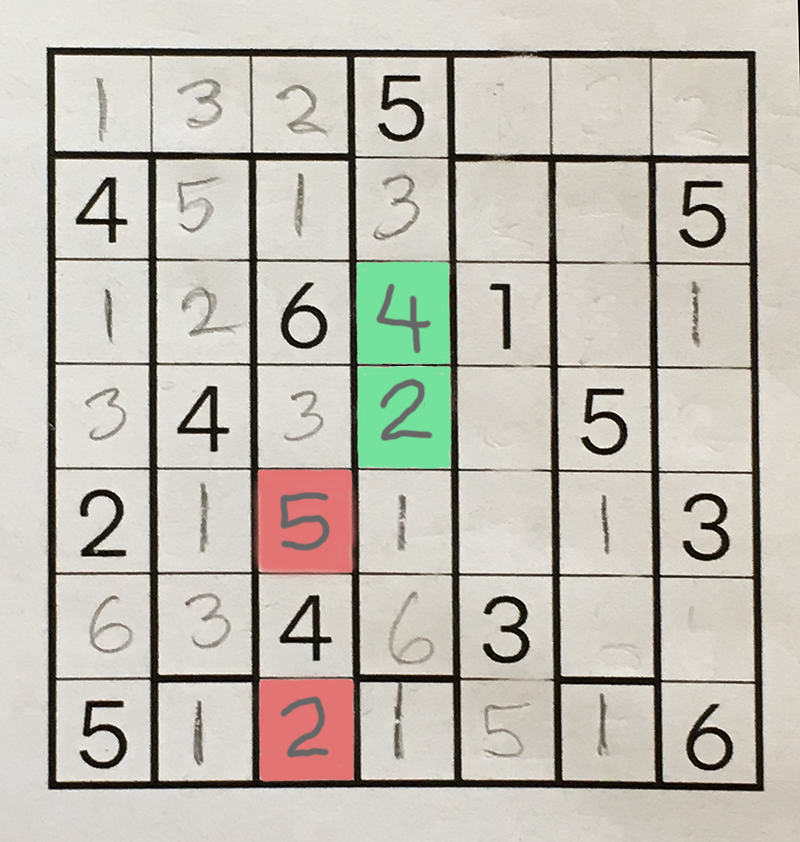
How do I justify that choice? Suppose the green 2 and 4 were transposed:
Then the pink 2 and 5 could be placed in either permutation, and no later moves elsewhere in the puzzle would ever resolve the ambiguity. This outcome is not acceptable if we assume the puzzle must have a unique solution. The uniqueness constraint might be expressed as a third rule:
- A number can be placed in a square if it is needed to prevent other squares from having multiple legal configurations.
I have vague qualms about this mode of puzzle-solving. It’s surely not cheating, but the third rule has a different character from the others. It exploits an assumed global property of the solution, rather than relying on local interactions. We are not making a choice because it is forced on us; we are choosing a cofiguration that will force a choice elsewhere.
In this particular puzzle it’s not actually necessary to apply the uniqueness constraint. There is at least one other pathway to a solution—which I’ll leave to you to find. Can we devise a puzzle that requires rule 3? I’m not quite sure the question is even well-formed. All constraint-satisfaction problems can be solved by a mindless brute-force algorithm: Just write in some numbers at random until you reach a contradiction, then backtrack. So if we want to force the solver to use a specific tool, we somehow have to outlaw that universal jackhammer.
The uniqueness constraint is not unique to the Capsules puzzle. I’ve encountered it often in kenkens, and occasionally in sudokus. I even have a sense of deja lu as I write this. I feel sure I’ve read a discussion of this very issue, somewhere in recent years, but I haven’t been able to lay hands on it. Pointers to precedents are welcome.
Addendum 2017-03-19: Jim Propp reminds me of his marvelous Self Referential Aptitude Test. The instructions begin:
The solution to the following puzzle is unique; in some cases the
knowledge that the solution is unique may actually give you a short-cut
to finding the answer to a particular question.
I completed the 20-question puzzle when SRAT first went public some years ago. This morning I found I was able to do it again with no diminution in enjoyment—or effort. I remembered none of the answers or the sequence of deductions needed to find them.
Highly recommended. And while you’re at it, check out Propp’s Mathematical Enchantments blog and his Twitter feed: @JimPropp.

I use this sort of reasoning all the time to help me solve sudokus and some other logic puzzles. I posted about it in 2005: see http://11011110.livejournal.com/23221.html and an earlier post linked from there.
Yes! Thank you. Your two posts are indeed what I was trying to remember. And well worth rereading 12 years later.
This comes up as well in the puzzle Alcazar. As you say, some people find using the promise of uniqueness a little risque:
https://www.theincrediblecompany.com/2014/11/13/introducing-the-ball-rooms/
On the other hand, there are lots of situations where we can reliably assume that the solution is unique: for instance, in cryptography, where there is a unique plaintext corresponding to the encrypted message. It seems reasonable to use this information when we have it…
…but it would also be nice to know that we can confirm it a posteriori. What if the puzzle-maker is lying, and there is more than one solution? In that case, we could have a cute situation where using uniqueness logic leads to a contradiction, making you think there is no solution at all!
- Cris
Alacazar is totally new to me, and it looks like fun.
As for the puzzle that punishes you for assuming it has a unique solution, I think you can create such a beast from the Capsules puzzle shown above by changing two of the givens. As you say, it’s a cute trick. But if I encountered it in the Times, I would write a complaining letter to the puzzles editor.
One-time-key cryptography relies for its security on never using the same key twice (they key is both endless and senseless), and so every possible decryption of the same length is indeed possible. It is as far as I know an unsolved problem to find an algorithm which can encrypt plaintext in such a way that two plausible decrypts exist: part of the trouble is the vagueness of “plausible”.
Actually, I recently learned from Alex Russell about a clever construct called “deniable encryption.” You can encrypt a message in such a way that, if caught by the authorities, you can “reveal” a different key than the true one, which decrypts your message to an innocuous plaintext. In essence, you’re using the non-uniqueness of the solution to hide the solution you want to keep hidden.
I don’t know if anyone has used this in practice, but it seems interesting…
I find it astonishing that deniable encryption is possible — except in the case that John Cowan mentions, with a key length equal to the length of the plaintext and ciphertext. But then again I’m amazed by almost everything that’s come out of cryptology in the past 50 years: homomorphic encryption, zero-knowledge proofs, all the way back to the original idea of public-key encryption. None of these things would be possible, if the universe had the orderly logical character I once thought it did.
But I do still wonder about the practical safety of such schemes. When the interrogator demands the secret key and threatens you with the rubber hose, you have to consider the possibility that he too knows about deniable encryption, and may not be satisfied with an innocuous message, whether or not it’s the correct decryption. In the case of the one-time pad, where any decryption is possible, the interrogator can just make up his own incriminating key.
Given the exact description of the puzzle
the setter would be within their rights to make a puzzle without a unique solution. So one can’t use the uniqueness of the solution, because that’s not a given.
But of course it is always a valid approach to guess the contents of some square and the proceed until one solves the puzzle or reaches a contradiction. So you can still solve the puzzle using exactly the same steps as you would have done using the uniqueness assumption. It’s just that you don’t think
but rather
while you proceed to put exactly the same numbers in exactly the same squares.
I wonder if one could make a fun type of puzzle which didn’t have a unique solution. One could arrange matters so that most guesses eventually lead to a contradiction, so that the skill would be in penciling in numbers which were part of a global solution. It would have a rather different feel to it than most puzzles.
Yes, it’s true the instructions give no explicit promise of uniqueness. But the next week’s paper will publish “the” solution, which is a pretty strong implicit claim of uniqueness. As I said above in reply to Cris Moore, if I found such a puzzle with multiple solutions, I would complain to the editor.
Well, if the puzzle editor is a nasty piece of work, they would publish puzzles where the number of solutions is anywhere from zero to, say, three, and publish all of the solutions (or the fact that there aren’t any) the following week.
But if there are no solutions, the puzzle solver should be required to find a proof of that fact… of course, the nice thing about puzzles is that the “certificate” of a solution is the solution itself, which fits on the page, while a “certificate” of unsolvability might be exponentially large. In CS terms, coNP and NP are probably different.
Even worse: if there are multiple solutions, the solver should be required to prove that they found all of them!
It seems that today’s capsule puzzle might need this condition of uniqueness. It’s the first puzzle in this series where the solution doesn’t seem completely determined. At least not that I see yet!
I found that puzzle very difficult; I had to set it aside overnight. But I was eventually able to finish without needing a uniqueness heuristic.
While uniqueness is expected, we do not need to rely on it to solve this puzzle.
If we use Excel labels, top row is 1, second row 2, etc., and left column A, next column B, etc., then cells E1 F1 G1 must contain numbers 1 and 2 and 3 somewhere. The region F2:F6 has 5 cells, 1 and 5 have been decided. F2 could be 2 or 3 or 4, except that we just eliminated 2 and 3 from consideration. F2 must be 4. We continue and decide F3 must be 3 and F6 must be 2.
Next consider the region E2:E7. Given certain cells have been decided, E5 could only be 4. This means D4 cannot be 4, which means D3 must be 4, leaving D4 to be 2.
My final solution is this, without relying on the unique solution rule.
1 3 2 5 1 3 2
4 5 1 3 2 4 5
1 2 6 4 1 3 1
3 4 3 2 6 5 2
2 1 5 1 4 1 3
6 3 4 6 3 2 4
5 1 2 1 5 1 6
Quoting myself:
Your sequence of moves is the pathway I had in mind.
Uniqueness is not required to solve the above puzzle. Just get further on the right side and the middle (highlighted) squares fall into place. I did the puzzle in roughly the same order, getting to where you left off in pencil, but then had to side-step over to the right side for a bit. The below link shows the grid solved, with the colors denoting the rough order I solved it - starting in red, and proceeding in rainbow order, changing color every so often. The pencil in the OP comprises red, orange, yellow. Then head over to green on the right to keep things moving. The first green I filled in was the 4 in the second row.
https://drive.google.com/open?id=0B8pzoCXo6SZyR2pTSG50ajR3bUU
Thanks for your note. Quoting myself again:
Your sequence of moves is the pathway I had in mind.