Mrs. Nguyen’s prestidigitation

From a set of 1 through 9 playing cards, I draw five cards and get cards showing 8, 4, 2, 7, and 5. I ask my 6th graders to make a 3-digit number and a 2-digit number that would yield the greatest product. I add, “But do not complete the multiplication — meaning do not figure out the answer. I just want you to think about place value and multiplication.”

The problem above comes from Fawn Nguyen, who teaches math at a public school in southern California and writes a blog called Finding Ways. To her students she is “Mrs. Win,” an English approximation to the Vietnamese pronunciation.

It’s clear that much care and craftsmanship went into formulating this problem. Why did Nguyen choose a two-digit-by-three-digit product, rather than two-by-two or three-by-three? The asymmetry ensures a unique solution. Why did she use playing cards to select the digits, rather than simply asking the kids to call out numbers? The cards produce a set of distinct digits, without duplicates, and they also rule out the possibility of choosing zero. Repeated digits or zeros would not ruin the problem, but they would needlessly complicate it. Nguyen’s classroom procedure eliminates these distractions without even mentioning them. This is the kind of subtle indirection you find in the performance of a first-rate stage magician.

I’ve had some serious fun with Nguyen’s problem. Finding the answer is not difficult—especially if you cheat and set aside her boldfaced injunction forbidding arithmetic. But of course the answer itself isn’t the point, as Nguyen makes clear in her blog post describing the students’ search for a solution. What we really care about is why one particular arrangement of those digits yields a larger product than all other arrangements. We want an explanatory pattern or principle, a rule that works not just for this one set of digits but for any instance of the max-product problem. I had many stumbles on the path to finding such a rule. Here are some notes I made along the way. But before reading on you might want to write down your own best guess at the answer.

1. First, some notation. Let’s label the digits like so:

   \[\begin{align}
   x_{2}\; x_{1}\; x_{0}&{}\\
   \underline{\times \quad y_{1} \; y_{0}}&{},
   \end{align}\]

   where the subscripts encode the power of 10 associated with each digit. The object is to find a one-to-one mapping between the sets \(\{x_{2}, x_{1}, x_{0}, y_{1}, y_{0}\}\) and \(\{8, 4, 2, 7, 5\}\) that maximizes the product.

2. Nguyen’s sixth graders were quick to perceive one important principle: Larger digits should generally go to the left, and smaller digits to the right, in order to get the most benefit from place values in decimal notation. No one proposed 258 × 47 as the maximum product; that combination is obviously beaten by 852 × 74.
3. If we wanted to solve this problem by exhaustive search, how exhausting would the search be? There are \(5! = 120\) permutations of the five digits, and each permutation corresponds to a different multiplication problem. But in view of the observation made in item 2, the number of plausible candidates is much smaller: just \(\binom{5}{2} = \binom{5}{3} = 10\). You could check them all in a matter of minutes. (But Mrs. Nguyen would not approve.)
4. Again following the logic of item 2, we can stipulate that the 8—the largest of the five digits—must wind up either in position \(x_2\) or in position \(y_1\). The question is which. My first thought was that surely the 8 goes in the three-digit number, because position \(x_2\) gives the 8 a value of 800, whereas it’s only worth 80 as \(y_1\).
5. My second thought undermined my first thought. Suppose the problem had been formulated without Mrs. Nguyen’s clever card trick, and we had to work with the digits 8, 7, 0, 0, 0. Then the arrangement yielding the maximum product is surely either 800 × 70 or 700 × 80. But of course those two products are both equal to 56,000. In other words, if we consider just the leading digits, it doesn’t matter which goes in the multiplier and which in the multiplicand.
6. Let’s write out the full six-term polynomial defining the product:\[1000 x_{2}y_{1} + 100 x_{1}y_{1} + 10 x_{0}y_{1} + 100 x_{2}y_{0} + 10 x_{1}y_{0} + x_{0}y_{0}\]The leading term provides another way of understanding why the largest digit can be either \(x_2\) or \(y_1\). It’s just the commutative law. We get \(1000 x_{2}y_{1}\) with either ordering. Thus we need to consider the smaller terms to decide which placement is better. Hint: \(y_1\) appears in three terms but \(x_2\) turns up in only two.
7. Maybe it would help to look at a smaller version of the problem? For example, maximize the product \(x_{1}\, x_{0} \times y_{0}\) with digits drawn from the set \(\{1, 2, 3\}\). Where does the largest digit belong?
8. Here’s a vague, daydreamy notion: The task of maximizing the product of these numbers looks something like an isoperimetric problem. If you have a rectangle of perimeter \(2(h + w)\), you maximize the area \(hw\) by making \(h=w\), so that the rectangle becomes a square. Maybe, by analogy, we should make the three-digit and the two-digit numbers as close to equal as possible, while at the same time making both of them as large as possible.
9. At this point I was ready to commit. I was persuaded by the arguments in items 6 and 7, and 8 that the largest digit should be bound to variable \(y_1\), and the next largest to \(x_2\). Then the same rule could be applied recursively to the remaining digits and variables, yielding this assignment:

   \[\begin{align}
   7\, 4\, 2&{}\\
   \underline{\times \quad 8 \, 5}&{}\\
   6\, 3\, 0\, 7\, 0&{}
   \end{align}\]

10. Of course you already know I was wrong. Even if you haven’t yet solved the problem for yourself or looked up the answer elsewhere, it’s a well-established principle of proper storytelling that no one ever stumbles on the right answer on the first try.

    My error was revealed by a program running an exhaustive-search algorithm. It showed that exchanging the positions of the 7 and the 8 yields a larger product:

    \[\begin{align}
    8\, 4\, 2&{}\\
    \underline{\times \quad 7 \, 5}&{}\\
    6\, 3\, 1\, 5\, 0&{}
    \end{align}\]

    But that isn’t the right answer either. Instead of switching the 7 and 8, you can exchange the 5 and the 4 to get the following result, which does turn out to be optimal:

    \[\begin{align}
    7\, 5\, 2&{}\\
    \underline{\times \quad 8 \, 4}&{}\\
    6\, 3\, 1\, 6\, 8&{}
    \end{align}\]

So that’s it—the answer we’ve been seeking, the maximum product, the solution to Mrs. Nguyen’s problem. There’s no arguing with arithmetic.

But it’s hardly the end of the trail. Why does that peculiar permutation of the digit set gives the biggest product? Does the same pattern work for other two-digit-by-three-digit products? What about problems of other shapes and sizes? And what is the pattern, anyway? How would you succinctly state the rule for placing digits in Mrs. Nguyen’s boxes?

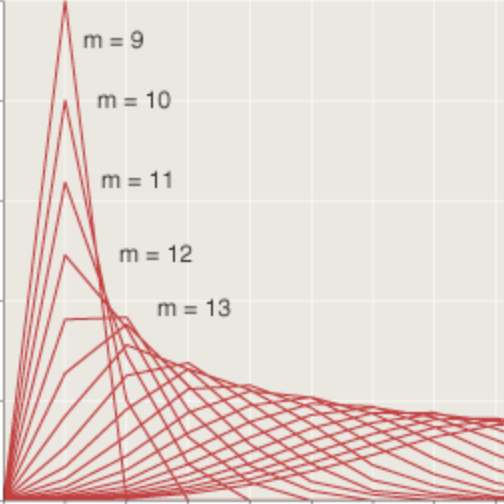
In trying to make sense of what’s going on here, I’ve found a certain graphic device to be helpful. I call it a lacing diagram, because it reminds me of the various schemes for lacing up a pair of sneakers. The patterns are easier to perceive with larger numbers of digits (i.e., high-top sneakers), so the examples given below show sets of 10 digits arranged to form a five-by-five multiplication problem.

In a lacing diagram the red arrows trace a path that threads its way through all the digits, ordered from largest to smallest. Each segment of this path can either cross from one factor to the other (a trans step) or stay within the same factor (a cis step). The particular lacing shown here is made up of alternating trans and cis segments. The sequence of t’s and c’s below the diagram serves as a linearized encoding of the pattern; the number below the encoding is the product of the two factors.

Here is the lacing diagram corresponding to the pattern that I initially believed would prevail in all Nguyen products:

In this case, all the steps are trans, as the arrows zigzag from one side to the other. The linear encoding consists of nine t’s.

And finally here is the lacing diagram for the winning permutation, the arrangement that gives the largest product. The pattern is the same as the second lacing diagram above—the zigzag—except for a single twist: The leftmost digits of the two factors have been switched, and so there is one cis step in the path.

After a bit of puzzling, I was able to work out why that single twist yields a better score than the plain zigzag. It’s because \((9 \times 7) + (8 \times 6) = 111\), whereas \((9 \times 6) + (8 \times 7) = 110\). Likewise \((9 \times 5) + (8 \times 4) = 77\), whereas \((9 \times 4) + (8 \times 5) = 76\), and so on. Note the difference between the twisted and the zigzag products: \(8439739020\, - 8428629020 = 11110000\). Each of the four pairings of the leftmost digits with those to their right contributes a 1 in that difference.

If one twist is a good thing, maybe more twists would be even better? For example, if we invert the 5 and the 4, we get \((5 \times 3) + (4 \times 2) = 23\) instead of \((5 \times 2) + (4 \times 3) = 22\), again for a net gain. But of course there’s a flaw in this strategy. Flipping the 5 and the 4 increases their products with neighboring digits to the right, but lowers those with digits to the left. Flipping the leftmost digits doesn’t run afoul of this rule because there are no neighbors to the left.

For a more explicit definition of the zigzag-with-a-twist arrangement, here is a Python implementation. The basic idea is to deal out the digits alternately to the \(x\) and \(y\) factors, starting with \(x\) and working through the digits in descending order. When \(y\) (the smaller factor) runs out of room, any remaining digits are tacked onto the end of \(x\). Finally—this is the twist—the leftmost \(x\) and \(y\) digits are swapped. This procedure works in any base.

def twisted_zigzag(digit_set, s):
    s = min(s, len(digit_set) - s)    # len of smaller factor
    digits = sorted(list(digit_set))  # smallest to largest
    x = []
    y = []
    while digits:                     # pop from end of list
        x.append(digits.pop())        # start with x
        if len(y) < s:                # zigzag until y is full
            y.append(digits.pop())
    x[0], y[0] = y[0], x[0]           # swap first digits
    return x, y

Does the zigzag-with-a-twist arrangement give the maximum product for all possible Nguyen-type problems? I can offer substantial evidence supporting that proposition. For base-10 numbers formed without repeated digits there are 4,097 two-factor multiplication problems with digits sorted in descending order. The zigzag-twist pattern gives the correct result for all of them.For digit sets that include 0, the solution is not always unique. Indeed, the algorithm works for all problems in bases between 2 and 15. It’s hardly a daring conjecture to suggest that it works in all bases, but I have not produced a proof. Maybe Mrs. Nguyen’s sixth graders will do so.