Years ago I lived in a house with a rhododendron outside the kitchen window, which served as our family thermometer on winter mornings. If the leaves were tightly rolled, you bundled up in gloves and scarf and ski cap; if not, just a jacket would do.

Rhododendron leaves with the temperature at 35º Fahrenheit (left) and 17º Fahrenheit (right).
Where I live now, we have a rhododendron by the front porch, and I’ve been keeping an eye on it for the past two winters. The qualitative relation between temperature and leaf-rolling is just as I remembered it, but I’ve been trying to add some quantitative precision. Can a rhododendron bush serve as a reliable temperature-measuring instrument? To find out, I bought a set of calipers, and I’ve been making daily measurements whenever the early-morning temperature is near or below freezing.
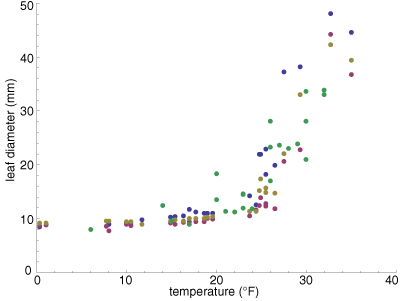
Here’s what the data look like (right). Each dot gives the diameter of a leaf, measured at its widest point, as a function of ambient temperature. The four colors distinguish measurements of different individual leaves. Last year I followed a single leaf (green dots); this winter I’ve been tracking three leaves I marked by wrapping twist-ties around the stems (tan, blue, magenta). If you’d like a look at the raw data, grab the csv file.
The overall shape of the relation is clear from the graph: Measured diameter increases monotonically with temperature, as expected. But there’s a fair amount of noise, as well as a sharp kink in the curve. If I had continued measurements to higher temperatures, we would surely see a second bend in the trend line. The full curve must be S-shaped, because the diameter of a rolled leaf has a finite maximum and minimum. No matter how high the temperature, the diameter can’t be greater than the width of the flattened leaf, and no matter how low the temperature, the diameter is bounded above zero.
Given the sigmoid shape, the right model for this data set is presumably a logistic curve, but I have done something simpler. I’ve partitioned the data into cold and warm subsets 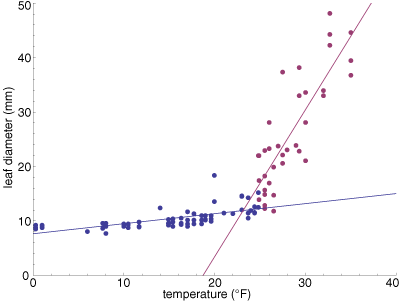 and fitted two piecewise linear functions. In the figure at left the data points are recolored to indicate which points go with which line. The crossover between the two functions is at 24.8 degrees, which maximizes the total R2 goodness-of-fit for the two lines.
and fitted two piecewise linear functions. In the figure at left the data points are recolored to indicate which points go with which line. The crossover between the two functions is at 24.8 degrees, which maximizes the total R2 goodness-of-fit for the two lines.
The kink in the curve is quite sharp. It remains visible after a log transformation, or even log log. Perhaps there’s a real, physical discontinuity there. After all, it’s not unreasonable to suppose that the freezing point of rhododendron sap might be somewhere around 25°F—although I don’t actually know that a phase transition has anything to do with the behavior of the leaves.
As a practical matter, the nonlinearity is an inconvenience if we want to use the leaves as a thermometer. It’s probably best to regard the rhododendron as a simple binary indicator: Either it’s cold out, or it’s not.
My hiking friend Dinosaur has told me about a wilderness school for teenagers with a rule that the kids have to stay in camp whenever the temperature is below 16°F. When this rule was announced, the camp leader complained: “We’re in the wilderness; we don’t have a thermometer.” The reply was: “Just use the rhododendrons.” That’s a wonderful suggestion. However, even with careful measurements of the leaves, it might be hard to gauge the temperature accurately in the range between 10° and 20°. And I suspect that a hiking group without a thermometer also lacks vernier calipers.
In the course of my morning measuring-the-rhodo rituals, I became curious about the mechanism of this temperature-sensitive leaf rolling. An analogy that immediately comes to mind is the bimetallic strip, often used as a temperature sensor in thermostats and oven thermometers. The idea is to bond layers of two metals (typically brass and steel) that have different coefficients of thermal expansion. With heating or cooling, one side expands or contracts more than the other, and so the strip curls up.
 Maybe the rhododendron leaf works this way too, with materials on the upper and lower surfaces that differ in thermal coefficient. But there are problems with this hypothesis. In the first place, a bimetallic strip curls end to end, not side to side. In other words, the axis of curvature is parallel to the shorter dimension; indeed, the device is fabricated as an elongated strip to avoid compound curvature, which could lead to buckling or other complex dynamics. If the same mechanism were at work in the rhododendron leaf, it would curl up from tip to stem, but in fact the curling axis is parallel to the long dimension of the leaf. It rolls up like the wrapper of a cigar. Another objection to the bimetal analogy is that really hot weather ought to cause curling in the opposite direction, with the underside of the leaf outermost. I’ve never seen that happen. Still another issue: The amount of curvature implies a huge difference in coefficient of expansion. In the photo above, a dissected leaf in near-zero-degree weather is rolled up tightly enough that opposite edges have passed each other once and are almost meeting for the second time.
Maybe the rhododendron leaf works this way too, with materials on the upper and lower surfaces that differ in thermal coefficient. But there are problems with this hypothesis. In the first place, a bimetallic strip curls end to end, not side to side. In other words, the axis of curvature is parallel to the shorter dimension; indeed, the device is fabricated as an elongated strip to avoid compound curvature, which could lead to buckling or other complex dynamics. If the same mechanism were at work in the rhododendron leaf, it would curl up from tip to stem, but in fact the curling axis is parallel to the long dimension of the leaf. It rolls up like the wrapper of a cigar. Another objection to the bimetal analogy is that really hot weather ought to cause curling in the opposite direction, with the underside of the leaf outermost. I’ve never seen that happen. Still another issue: The amount of curvature implies a huge difference in coefficient of expansion. In the photo above, a dissected leaf in near-zero-degree weather is rolled up tightly enough that opposite edges have passed each other once and are almost meeting for the second time.
The magnitude of the curling effect suggests there may be something more than just thermal expansion and contraction going on. Likewise the kink in the temperature-diameter curve hints at some discontinuous process. And the axis of curvature has me wondering about the possibility of a structural asymmetry—something that inhibits lengthwise curling and favors crosswise.
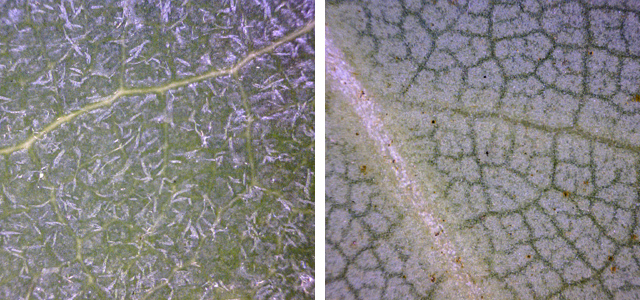
In the search for asymmetry, I pulled out the microscope. The images above show the upper (left) and lower (right) surfaces of a leaf at 30 times magnification. I see no network of crosswise contractile fibers. The only distinctively asymmetric structure is the leaf’s stout central vein—a continuation of the stem—but maybe that’s all we need. The central vein might be strong enough to inhibit lengthwise curling in the initial stages of the process, at temperatures near freezing, when the curling forces and the resulting curvature are slight. Later, the crosswise curling creates a tube, which offers mechanical resistance to lengthwise bending as the curling continues. But all this is just speculation.
A little casual Googling turns up lots of stuff on the folklore of rhododendrons as weather indicators, but the only scholarly discussion I’ve stumbled on is a 1990 article by Erik Tallak Nilsen of Virginia Polytechnic in Blacksburg (where lots of rhodos grow). Nilsen doesn’t have much to say about how the leaves curl; he’s interested in why. The widely prevalent theory—often stated as established fact—argues that leaf-rolling helps prevent water loss by covering the pores (called stomata) on the underside of the leaf. Nilsen doesn’t think much of this idea. He points out that the stomata close in cold weather, sealing off the moist internal milieu. And he backs up this assertion with his own experimental results.
Among several alternative explanations, Nilsen favors the following idea: Rhododendrons live in the understory of hardwood forests, where they are shaded in summer but exposed to full sunlight after the trees drop their leaves in winter. The photosynthetic membranes of shade plants are susceptible to damage from ultraviolet light, especially in freezing weather. Rolling the leaves reduces the exposed area.
One of the best essays I’ve read in a long time. Thanks!
Intriguing observation!
My first thought was that this may also be a humidity or amount-of-sunlight effect, rather than an immediate effect of temperature (although both variables may be correlated with temperature): in autumn, (some) dry leaves tend to curl up and clover leaves role up when the sun sets. So, it may be worthwhile to do a Google Scholar search for why plant leaves role in general, and then try to identify which mechanism is at work in rhododendrons.
Since you found no lateral asymmetry, I speculate that the curling comes from an asymmetry between (the humidity response of) the upper and lower side of the leaves. It is much like your bimetal analogy, except that in my hypothesis it is the more/less hydration that causes the tension by thickening/thinning the sides. (So, it may still be related - somehow - to the stomata: if they are present preferentially on one side of the leaves, or if their closure rates are different on both sides, the rate of evaporation is different, which may cause one side to dehydrate faste, which may create enough tension to make the leaves curl up partially.)
Maybe humidity gives an even cleaner fit to rhododendron curling? (Although the goodness of fit in your results is already quite impressive!) I assume that there is a strong correlation between ambient temperature and air humidity, but not a perfect one. (The maximal humidity - before condensation starts - increases as temperature increases; so, hot air can contain more water vapour, but it won’t be maximally humid every day.)
In other words, it would be interesting to have humidity measurements as well as temperature data and rho-curl. Are you up for that? :-)