The printed program for the recent STOC meeting in Cambridge announced the following talk:

Unfortunately, the fourth author could not be present (and he is not listed as an author on the paper itself), so the talk was given by Gregory Valiant.
Here is a motivating example. Take a tape measure, and go record the heights of a few thousand adults chosen at random. You’ll come back with a distribution that looks something like this:
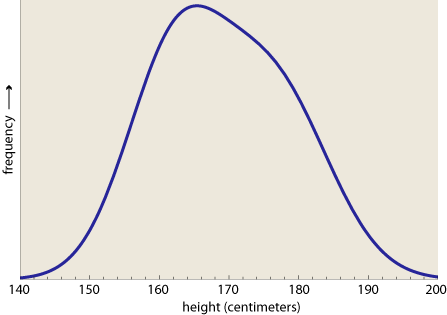
How come the curve is so lumpy and lopsided? Isn’t height a variable with an approximately normal distribution? Of course it is. The problem is that we have mixed up two subpopulations—men and women—with different height distributions:
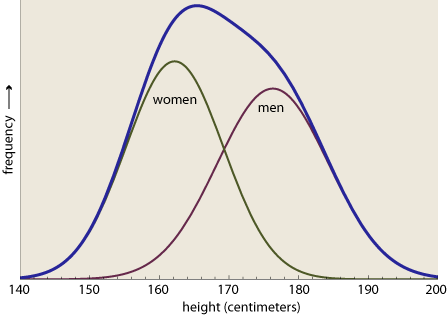
Question: Given the lumpy combined distribution, and the knowledge that it represents a mixture of exactly two normal distributions, can we somehow recover the component distributions? Specifically, can we determine the means and standard deviations and the Gaussian curves, as well as their relative weights, or contributions to the total?
The answer is yes. In a series of papers published in the 1950s and 60s, Henry Teicher (then at Purdue, now emeritus at Rutgers) proved a kind of unique-factorization theorem for distributions. He showed that no mixed distribution can be decomposed into two or more different sets of normal distributions, just as no composite whole number can be formed as the product of two or more distinct sets of primes. (Teicher’s theorem generalizes to many distributions other than normal ones. There are also a few caveats; for example, none of the component distributions can be pointlike, with a standard deviation of zero.) Teicher’s work implies that a mixed distribution is identifiable: If you can break it down into a set of primitive distributions, then that decomposition is unique.
If STOC were a mathematics meeting, that might be the end of the story. But STOC is the Symposium on the Theory of Computing, and the question here is not “Does a solution exist?” but rather “Can you solve it in polynomial time?” Teicher’s result offers no such guarantee. It turns out that his proof of identifiability depends on the behavior of the distributions far out in the tails. Measuring data frequencies in these sparsely populated outlying regions requires an exponentially large number of samples. But other approaches to the problem don’t run into this snag; Valiant and his colleagues show that “robust polynomial identifiability” is indeed possible.
A key idea in their proof goes back at least as far as the 1890s, to work done by the indefatigable statisticians W. F. R. Weldon and Karl Pearson. In 1892 Weldon spent a summer on the Bay of Naples, measuring various features on the carapaces of crabs. One such feature yielded a distinctively lumpy distribution much like the height curve shown above. Weldon thought that the asymmetry might signal the incipient splitting of the crab population into two races or species, each of which if taken individually would have a normal distribution. For help with the analysis of his data he turned to Pearson, who was able to identify two component Gaussian curves that sum up to the observed distribution. (The figure comes from Weldon’s 1893 paper; see below for references.)
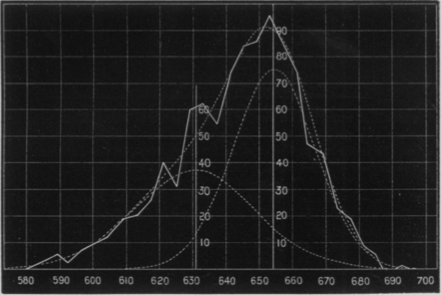
Pearson’s method was based on calculating the first six statistical moments of the given distribution. (The nth moment of a distribution is the expectation value of \((x-\bar{x})^n\), where \(x\) is a random value drawn from the distribution and \(\bar{x}\) is the mean value.) The process called for solving a ninth-degree polynomial, which was a heroic feat in 1893.
Valiant et al. show that a procedure like Pearson’s will always succeed in the following sense: If two mixed distributions can be distinguished at all, then they can be distinguished by examining their first six moments, and those moments characterize the component Gaussians. Calculating the moments requires only a polynomial number of samples, and the running time of the overall algorithm is a polynomial function of various parameters such as the required accuracy. Moreover, the process can be extended from one-dimensional distributions to multidimensional Gaussians.
Although the algorithm has polynomial running time, that’s not a guarantee of practicality. (After all, this is a theory conference.) One stage of the process is essentially a brute-force search through a very large (though polynomially bounded) space of parameter values for the six moments.
Sources:
The STOC proceedings with the Kalai-Moitra-Valiant paper are now available online, but only by subscription. A PDF preprint is posted on Valiant’s web site; also an expanded version.
For Henry Teicher’s work see: “Identifiability of Mixtures,” The Annals of Mathematical Statistics 32(1):244–248 (1961) and “On the Mixture of Distributions,” The Annals of Mathematical Statistics 31(1):55–73 (1960).
For Weldon and Pearson see: W. F. R. Weldon: “On Certain Correlated Variations in Carcinus maenas,“ Proceedings of the Royal Society of London 54:318–329 (1893) and Karl Pearson: “Contributions to the Mathematical Theory of Evolution,” Philosophical Transactions of the Royal Society of London A 185:71- 110 (1894).
My thanks to Virginia Gold and Irene Frawley at ACM, Lance Fortnow, Paul Oka, Jennifer Chayes and Christian Borgs, all of whom helped make it possible for me to attend some of the STOC sessions.

Sounds applicable to performing photometry on images containing rich star fields where individual stars overlap. The usual technique uses deconvolution but assumes each star adheres to the same known Gaussian PSF (point spread function). More recent work (Magain, et al, 2007) solves simultaneously for the individual Gaussians and the PSF but still assumes the PSF is the same for all stars which becomes less likely as the image grows larger in size.
I included a link to this post in Carnival of Mathematics #67.