A shy woodland creature

Martin Gardner died over the weekend. He was 95 and living in Norman, Oklahoma, not too far from his birthplace in Tulsa.

Like many others, I grew up on Martin’s “Mathematical Games” column in Scientific American. Later I joined the staff of that magazine—but don’t imagine that Martin and I became office buddies. As a matter of fact, I never once saw him in the office. He worked at home. He attended none of our editorial meetings. We never had lunch together. Indeed, I never would have met him at all except for the coincidence that we lived a few blocks apart, and every now and then I would be called upon to deliver a package of urgent proofs. (By the way, his address in those days was on Euclid Avenue!)

Someone on the magazine staff described Martin as “a shy woodland creature,” and the tag stuck. Looking back, however, I think it tells only half the story. Yes, Martin was no schmoozer, and he preferred to stay out of the spotlight, both in person and in print. Most of his best-known columns reported on someone else’s discoveries—Conway’s game of life, RSA’s cryptosystem, Penrose’s tilings. He delighted in annotating other people’s work, as in his celebrated edition of Lewis Carroll. Yet he was anything but timid or retiring. In an argument, the shy woodland creature was a grizzly bear. He had strongly held opinions and philosophical convictions, and he knew the worth of his own work. He was a man of ideas, to be taken seriously, yet also a man who had fun with his ideas.

As a celebration of Martin’s peculiar genius, I would like to revive the little puzzle that formed the basis of his very first column, in January of 1957. (He had published a few articles in Scientific American earlier, but this was the first column to appear under the “Mathematical Games” title.)

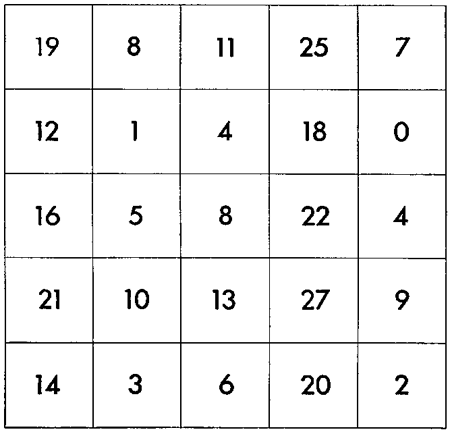
On the bingo card above, choose any number, circle it, and cross out all the other numbers in the same column or row. Now select a second number from among those that remain unmarked, and again circle your choice and then cross out the rest of the column and row. Continue in this way until there are no unmarked numbers left to choose.

The sum of the circled numbers is 57. How did I know that? How did Martin construct the matrix?

Update 2010-05-29: Here is Martin’s own explanation of the 1957 puzzle:

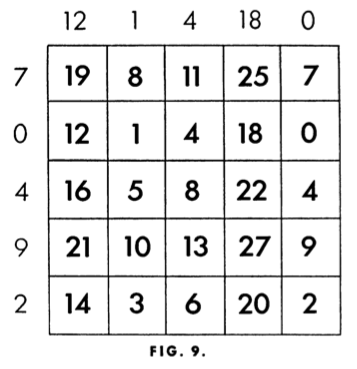
Like most tricks, this one is absurdly simple when explained. The square is nothing more than an old-fashioned addition table, arranged in a tricky way. The table is generated by two sets of numbers: 12, 1, 4, 18, 0 and 7, 0, 4, 9, 2. The sum of these numbers is 57. If you write the first set of numbers horizontally above the top row of the square, and the second set vertically beside the first column [see Fig. 9], you can see at once how the numbers in the cells are determined. The number in the first cell (top row, first column) is the sum of 12 and 7, and so on through the square.

You can construct a magic square of this kind as large as you like and with any combination of numbers you choose. It does not matter in the least how many cells the square contains or what numbers are used for generating it. They may be positive or negative, integers or fractions, rationals or irrationals. The resulting table will always possess the magic property of forcing a number by the procedure described, and this number will always be the sum of the two sets of numbers that generate the table.