All my closest friends know about my strange obsession with the mathematics of mattress flipping. A few thousand other people also know my secret, since I have written about it in an American Scientist column (HTML, PDF), which later became a chapter in a book.
To recapitulate: Fussy housekeepers rotate their mattress twice a year to ensure even wear. But a mattress has three axes of twofold symmetry (roll, pitch and yaw). Rotating around the same axis over and over will not cycle through all four possible states of the mattress, so you need to vary the procedure. Perhaps you do a roll one time and a yaw the next. But in the spring you may have forgotten which way you turned last fall. Thus the quest for a “golden rule” of mattress flipping:
A golden rule of mattress flipping would be some set of geometric maneuvers that you could perform in the same way every time in order to cycle through all the configurations of the mattress. Following this algorithm might entail extra physical labor on each occasion–perhaps making multiple flips or turns–but at least it would eliminate the mental effort of remembering.
The rules of this peculiar game forbid putting any marks on the mattress (which would break the symmetry). If we abide by this constraint, the multiplication table for the group of flip operations looks like this:
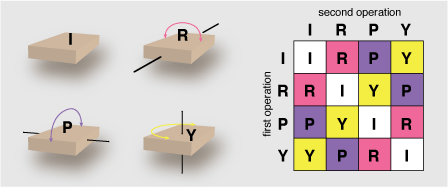
R, P and Y indicate half-turns around the roll, pitch and yaw axes; I is the identity or do-nothing operation. This table is bad news for golden rules. We already know that no single operation will cycle through all four states of the system, and the table shows that every combination of two operations is equivalent to some single operation. Hence there is no golden rule.
There the matter stood until a few days ago, when I received a letter from Tim Knoll:
I just completed reading your collection of columns entitled “Group Theory in the Bedroom” and I wanted to offer up an alternative solution to the mattress flipping problem. I believe if you add one more operation to the mattresses you can achieve your “golden rule.” What you need to add is a second bed to allow a shift operation in addition to the rotations. If you have the second bed oriented in the opposite manner as the first bed (with the first having the headboard facing north, the second facing south) you can simply have an operation of a non-rotating shift from the first (north-facing) bed to the second (south-facing) and then do a shift in addition to a rotate about the pitch axis from the south-facing bed to the north-facing bed. This mattress juggling should also achieve the desired results using the roll axis in the second step. I unfortunately can’t implement this method in my own apartment since it is equipped with one queen-sized bed and one full-sized bed, but my tests using an index card seemed accurate.
Ingenious, no? But is it truly a golden rule? I’m going to leave that question for readers to decide.
Knoll also points out that even if the new “shift” operation doesn’t yield a golden rule, it does succeed in getting two mattresses flipped with the same mental effort that would otherwise be needed for one mattress. This raises a further question: Why stop at two beds? What about mattress flipping in a barracks, where many beds are lined up in a row? And then there’s the job of flipping mattresses in the Hilbert Hotel, which has infinitely many beds. Does the mental effort per mattress go to zero in this limit?

Not sure about multiple beds but I thought the flipping scheme was pretty simple for a single bed. There are only 4 possible places for ones head to go on a two-sided, two-ended bed. Just mark each of these with the names of the seasons and when each season starts place the end with its name where you would like your head to be. If you miss a season, it all gets back in sync next season. Save your group theory for a tougher problem. ;-)
If you can alternate rolls and flips (say), you can arrange for any single mattress to have all of its orientations visited.
I do not understand Tim Knoll’s description, exactly… But his idea is sound. If you simply have a “ring” of two or more beds, and you roll each mattress as it enters bed 1 and flip it as it exits bed 1, then obviously each mattress will visit every possible orientation (because its own sequence of rolls and flips will alternate as it keeps passing through bed 1).
However, if you consider the combination of mattress orientation and bed number as the “state” of the mattress, then at least half of the total states will never be visited. In my example, for instance, “mattress A on bed 1″ will only be seen in half of the possible orientations. I do not believe this can be fixed without introducing memory into the protocol (or marking the mattresses).
This claim is not too hard to prove… Without memory, any rule involving moving mattresses among multiple beds reduces to a set of disjoint “rings” (cycles), where each bed has a fixed “next bed” and a fixed “next mattress operation” (I, R, P, or Y). Again, if you focus on a single mattress and a single bed, you can easily show it can only reach half of the possible orientations on that bed.
P.S. As for the Hilbert Hotel, my rule would be to move the mattress in room N to room N+1 for each N. If N is odd, roll the mattress; if N is even, flip the mattress.
Would my rule count as constant mental effort, or infinite mental effort?
Of course, you will need to keep adding new mattresses. The Hilbert is like that.
My solution to this is to toss a coin each time. Heads is a P (flip over the head), tails is an R. I flip mine everytime I change the valance though, (significantly more than once a season).
Unless you have taken the law into your own hands and removed the tag, the mattress is marked already. So if you confine yourself to rolling and yawing, both of which flip the side the tag is on, you can simply identify one side of the bed as the roll side and the other as the yaw side.
It shouldn’t be possible to find a “golden rule” to handle all possible mattress situations no matter how many mattresses you add: this would require the group of symmetries to be a cyclic group, but the group needs to have the symmetries of any single mattresses as a subgroup. The group of symmetries of the single mattress has three distinct elements of order two, which is impossible in a cyclic group.