Sudoku dans la Belle Époque
by Brian Hayes
Published 7 June 2006
A few weeks ago I commented on the discovery of some curious precursors of Sudoku, drawn up in the 1950s as designs for agricultural experiments. Now even earlier antecedants of the puzzle have been discovered by Christian Boyer, a specialist in recreational mathematics. Writing in the French magazine Pour la Science, Boyer describes and reproduces several puzzles originally published in French newspapers and magazines in the 1890s. None of these puzzles is a genuine Sudoku, but the family resemblance is striking. Several of them have nine-by-nine grids to be filled in with numbers, and a few of the nine-by-nine grids are subdivided into three-by-three blocks.

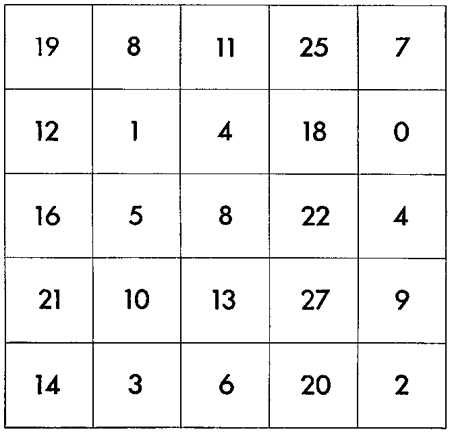
Among the many near misses, Boyer cites the puzzle shown at right as the closest known approach to a pre-invention of the Sudoku. (Image source: Christian Boyer.)
It was composed by B. Meyniel and published on 6 July 1895 in the daily newspaper La France. The instructions present the problem as a magic square, to be filled with the numbers from 1 through 9 so that all rows, all columns and all diagonals have the same sum (namely, 45). The three-by-three subgrids familiar to Sudoku players are not mentioned in the instructions or distinguished in the diagram. Nevertheless, if you try to solve the puzzle as if it were a Sudoku, you’ll find that it works: Each number from 1 through 9 appears exactly once in each subgrid. Actually, there are two such Sudoku solutions. (Meyniel’s rules exclude one of these solutions by requiring a “diabolical” magic square, in which the broken diagonals also yield the magic sum.)
Boyer presents several more fin de siecle puzzles that are Sudoku-like in one way or another. The text of his article (but not the illustrations) is available online from Pour la Science, and a supplementary document with more details and newspaper clippings is at Boyer’s web site.
Publication history
First publication: 7 June 2006
Converted to Eleventy framework: 22 April 2025