First Bites

In the game of Chomp, the player who moves first always has a guaranteed winning strategy. This fact might seem to take all the suspense out of the game, but it doesn’t. Except in the smallest and simplest games, no one knows which first move will lead to the guaranteed victory. For me, this situation makes playing Chomp doubly frustrating. When I go first, I have no excuse for losing—but lose I do, even to mindless players like this Java applet by Andries E. Brouwer. Some recent work has taken a new approach to understanding the difficulty of Chomp. The results won’t necessarily help you win, but they may help you understand why finding a winning move can be hard.

Chomp is played on a rectangular field divided into east-west rows and north-south columns. Initially, all the cells of this array are filled with markers such as checkers or cookies. A move consists of choosing a cell and removing the marker there as well as all the markers to the north and east of it—thus taking a rectangular bite out of the array from the northeast corner. On each turn you are required to remove at least one marker. The object is to avoid taking the last, “poisoned” marker, in the southwest corner, thereby forcing your opponent to swallow it. The game was invented in the 1970s by David Gale of the University of California at Berkeley. The name was coined by Martin Gardner.

How do we know that the first player can always win in Chomp? It’s beguilingly simple. Suppose you go first and take just the smallest legal bite—the single marker in the northeast corner. Then I respond with a countermove that turns out to be a winner—a move so good that no matter what you do in reply, you are inevitably stuck with the poison pill at the end of the game. Well, if my move is so unanswerably brilliant, why didn’t you choose it as your own? You could have won by making my move at the outset. This argument hinges on a property of Chomp that sets it apart from many other games of strategy, such as chess: If a move is legal at any time during a game of Chomp, then it is legal as an opening move.

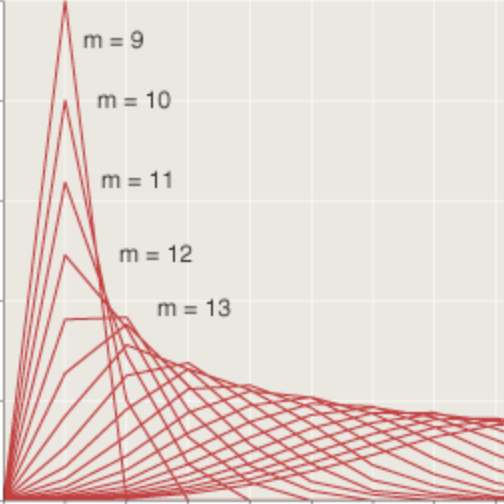
For a few special geometries it’s easy to find a winning strategy in Chomp. For square arrays and for shallow rectangles with just one or two rows, there are simple rules for choosing a move. Long rectangles with three or more rows, however, have resisted comprehensive analysis. Computational methods have identified the winning first move for thousands of specific array shapes, but they have failed to reduce the game to any simple formula. Below are the winning first bites in a few three-row games.

Note that the shape of the chewed-off rectangle varies from case to case.

In the past few years, three-row Chomp has been studied in detail by Doron Zeilberger and his students at Rutgers University. They have found no concise magic formula for winning the game, and yet the distribution of winning and losing moves is not random, either; there are strong regularities.

Any configuration of a three-row game can be mapped to a point in a three-dimensional space. The (x, y, z) coordinates of the point represent the number of columns occupied by three, two and one markers respectively, and each point in the space can be labeled as a winner or a loser. If the game had no ordering principle whatever, then winning and losing positions would be scattered completely at random within this volume. If there were some simple rule for winning (e.g., always choose y and z so that they are prime numbers), then obvious patterns would show up in the distribution of winning points. The truth lies somewhere between these extremes.

Zeilberger and his student Xinyu Sun defined sets of points they called “instant winner” positions. These are (x, y, z) points from which you can legally move to another point with a smaller value of x that turns out to be a loser. Zeilberger and Sun discovered that along certain lines within the space—lines where x and z are held constant but y increases—the distribution of instant-winner points starts out looking random but then seems to become “ultimately periodic,” with either a constant value or a simple repetitive pattern. The ultimate periodicity of the sequences was later proved by Steven Byrnes. (Byrnes was a high school student at the time. His proof won a $100,000 science fair prize, which is a lot more than most theorems earn for their authors. Byrnes is now an undergraduate at Harvard.)

Recently, the patterns observed in the (x, y, z) space of Chomp moves have been explored further by Eric J. Friedman of Cornell University and Adam Scott Landsberg of the Claremont Colleges. Their approach is quite different from the usual methods of game theory, number theory and combinatorics. They look upon the game as if it were a problem in physics, such as trying to understand the onset of magnetization in a metal or the growth of a crystal. Although the game itself is strictly deterministic—there is no rolling of dice in Chomp—Friedman and Landsberg are led to make probabilistic predictions about the winning chances of moves in various parts of the grid. In a physical system, it’s seldom possible to know all the details about the states of individual atoms, but one can nonetheless make reliable estimates of macroscopic properties. Likewise in Chomp, the exact location of winning and losing squares varies unpredictably with any small change in the initial configuration of the array, but the overall, large-scale geometry is highly consistent.

The diagrams reproduced here (courtesy of Friedman and Landsberg) show instant-winner positions for certain three-row games. Blue points are instant winners, tan points are not. The diagrams are slices through the (x, y, z) volume, the larger panel along the plane where x=700 and the smaller at x=350. What’s notable is the similarity of the two patterns—the solid wedge at the lower left, the salt-and-pepper cone at the upper left, the series of horizontal stripes (which correspond to Zeilberger’s ultimately periodic sequences). But the similarities are only present at large scale; the detailed distribution of the various stripes and other features changes totally from one diagram to the other. Friedman and Landsberg derive a “renormalization” procedure—an idea borrowed directly from physics—that can account for this persistence of large-scale structures even as all microscopic configuration becomes thoroughly mixed up. And they give a probabilistic prediction of where a winning play is most likely to be found.

For all the statistical flavor of Friedman and Landsberg’s analysis, they have one result that is not at all probabilistic. They prove that in three-row Chomp the winning strategy is unique; for any configuration of the game, there is one and only one move guaranteed to produce a victory.

Links::

• Friedman and Landsberg (PDF via ftp)
• Zeilberger 2001 and Zeilberger 2004
• Byrnes
• Andries E. Brouwer on Chomp

Deep Background:

• Gale, David. 1974. A Curious Nim-type game. American Mathematical Monthly 81:876-879.
• Gardner, Martin. 1973. Mathematical games: Sim, Chomp and Race Track: New games for the intellect (and not for Lady Luck). Scientific American 228(1):108-115.

Finally, thanks to Steve Strogatz of Cornell for alerting me to the work of Friedman and Landsberg.