The U.S. Supreme Court heard arguments the other day on programs meant to maintain racial diversity in the public schools of Seattle and Louisville. Listening to accounts of the debate put me in mind of Thomas C. Schelling’s elegant mathematical model of race relations. The model suggests that extreme segregation can arise spontaneously even when no one in the population desires that outcome. I wish I could submit a friend-of-the-court brief (although I’m not feeling very friendly toward this particular court).
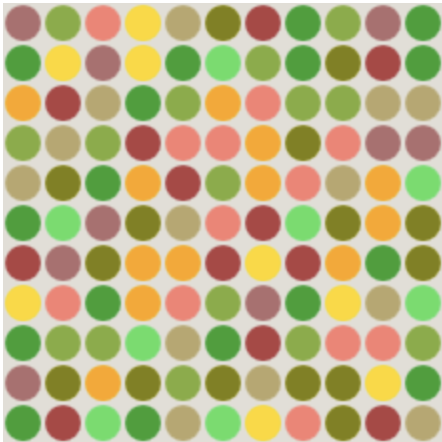
The panel at left shows four stages in the evolution of a simple version of Schelling’s model. Initially, equal numbers of individuals from two groups—they’re shown here as blue and tan, but I’m going to refer to them as black and white—are dispersed at random. Neither race seeks to escape or exclude the other; the only racial preference is of the mildest sort—a desire not to be entirely cut off from people of one’s own group. But that desire is enough to cause the two populations to separate like oil and water.
The simulation takes place on a two-dimensional lattice with N sites, occupied by M agents, where M < N, so that at least a few sites remain vacant. At each time step each agent examines the eight sites surrounding its position, calculating the proportion of neighboring agents that match its own color. If the proportion of same-race neighbors exceeds some given threshold β, the agent is contented and stays put. On the other hand, if the fraction of like-colored neighbors falls short of the threshold, the agent moves, choosing its new home at random from among the N – M vacant sites; in the process of moving, of course, the agent creates a new vacancy in its former position. The process is then repeated, stopping only if and when there are no more discontented agents.
The model has two parameters: the threshold of contentment β and the filling factor (the fraction of occupied sites, M/N). As each of these parameters increases from 0 toward 1, agents have a harder time finding a satisfactory home. The interesting region in parameter space is where the threshold β lies between about 0.25 and 0.5, and the filling factor is close to 1, so that there are few vacancies on the lattice. The high filling factor excludes solutions in which people get along by living in isolation. As for the threshold, it’s easy to find a pattern acceptable to all if no one minds being in the minority, but the challenge naturally gets harder as the agents become more discriminatory. Still, it’s important to note that even at a threshold of 0.5 (i.e., each agent wants to have at least half of its neighbors match its own color, and no one is willing to be in a minority) there is an obvious solution that makes everyone happy. That solution is a checkerboard pattern, which happens to represent a maximum of racial integration. But the checkerboard is not the pattern that typically emerges when the model is run from a random initial state. Instead, within a few hundred time steps, the two populations segregate themselves, forming large, amoeboid areas of racial uniformity. The sobering lesson of this simple model is that it doesn’t take deep-seated and vitriolic racism to produce a stark pattern of segregation; it’s enough that each of us feels uncomfortable when outnumbered. And the sharp color lines develop even though those who move don’t take race into account when choosing a new location.
For anyone who might care to experiment with the Schelling model, there are Java applet versions here and here (and probably more). The model is also among the demo programs included with several versions of the StarLogo and NetLogo programming languages.
Schelling’s model deals with residential racial patterns, but it’s not hard to adapt the same basic ideas to the study of segregation and integration in school systems, which was the issue before the Supreme Court this week. The main difference is that in the school case we need to look at a few large subsets of the population (the schools) rather than many small neighborhoods. In the scholastic variant of the Schelling model, a student attending a school where the proportion of his or her own race falls below the threshold β would transfer to a randomly chosen vacant place elsewhere in the system. Although I have not yet tried to build and run a computational version of this model, I think it’s possible to see what kind of behavior to expect, simply by considering the smallest nontrivial model: two schools of equal size, shared by black and white populations that are also equal. In this situation, if the fraction of white students in one school is r, then the fraction of black students in the same school must be 1–r, while in the other school the black fraction is r and the white fraction 1–r. Suppose r ≤ 1/2. Then any allocation of students for which r ≥ β will be agreeable to everyone. At the same time, there is another possible solution, namely r = 0, or total segregation, with one all-white school and one all-black school. As β approaches 1/2, the integrated solution becomes increasingly fragile and hard to maintain; at β = 1/2, the equilibrium is instantly destroyed by the slightest perturbation (such as someone moving into or out of the district); beyond β = 1/2 the shared-schools solution disappears, and only total segregation is feasible.
Does this simple-minded model have anything to do with the real-world plight of kids going to school in Seattle and Louisville? Both of those cities once had highly segregated schools and achieved a better racial balance only by means of deliberate incentives and policies, applied steadily over more than 30 years. In the case of Louisville, the desegregation plan was mandated and supervised by the courts from 1973 until 2000; since then, aspects of the program have been continued voluntarily as a means of maintaining racial diversity. In Seattle the measures were adopted by the school board without outside compulsion. Currently, Seattle’s 10 high schools have a citywide open-enrollment policy, so that any student can choose any of the schools. Those schools that have more applicants than places use several factors to determine which students will be admitted, including geography and the presence of siblings already attending the school. Racial balance is the final tiebreaker.
The students and parents who have challenged these policies (supported by an amicus brief from the Bush administration) argue that race should not be a factor at all in assigning children to schools—that it’s no more legimate to consider race as a way of achieving integration that it would be in maintaining segregation. In other words, policies must be colorblind, even though people aren’t.
We won’t know for months how the supremes will rule on this issue, but savvy court-watchers say the outlook is dim for the diversity policies; and if they are overturned in Seattle and Lousiville, similar programs will have to be dismantled in many other cities as well. What’s the appropriate response? One might well try to out-Herod Herod, taking the position that all school-assignment decisions (and analogous choices both within the schools and everywhere else in American life) should be conducted as a pure lottery. After all, if race is a forbidden criterion, how can we allow accidents of residence or wealth or personal history to intrude? This strategy has the virtue that it would make pretty much everyone fiercely unhappy—and so it probably wouldn’t last long.
For another approach to the problem, I would like to ask this: What could we change about Schelling’s model in order to get a somewhat brighter vision of the future? The obvious candidate is the model’s one-sided choice function. In the world of the Schelling model, we all want to avoid being too much in the minority, but no one worries about being too much in the majority. I’d like to think, on the contrary, that we might have at least a few people who go out of their way to seek diversity, who pull up stakes and move not only if they have too many neighbors of another race but also if they have too few. It would be interesting to explore the phase diagram of a model that included such a subpopulation.
A few references:
Schelling, Thomas C. 1971. Dynamic models of segregation. Journal of Mathematical Sociology 1:143–186.
Schelling, Thomas. C. 1978. Micromotives and Macrobehavior. New York: W.W. Norton.
Granovetter, Mark S., and Roland Soong. 1988. Threshold models of diversity: Chinese restaurants, residential segregation and the spiral of silence. In Sociological Methodology (edited by Clifford Clogg), pp. 69–104. PDF
Clark, W. A. V. 1991. Residential preferences and neighborhood racial segregation: a test of the Schelling segregation model. Demography 28:1–19.
Bruch, Elizabeth E., and Robert D. Mare. 2004. Neighborhood choice and neighborhood change. PDF
Aguilera, Antonio, and Edgardo Ugalde. 2006. A spatially extended model for residential segregation. http://arxiv.org/abs/nlin/0607026
Interesting post but it is not the job of the government to impose integration; in fact, the constitution prevents it. The assortment of people into segregated enclaves may happen, but I am not convinced it will.
Fascinating!
Do you have an idea how the simulation result might change if people could exit the system, if the whole system were continually growing, or if there were “magnet” nodes exerting countervailing force?
My own school system uses the proportion of students eligible for reduced-price or free school lunch as a yardstick for maintaining balance when attendance districts are drawn each year. This is a fast-growing school system, so new schools open each year and a lot of students move around.
We don’t seem to have a Schelling model: There is the parameter of choice, provided by magnet-schools offerings, and the parameter of growth. Both of these seem to keep individuals from being forced to make the either-or decisions (move-stay) embedded in the Schelling model. Or maybe it’s just harder to see, in this complex mix, patterns in the decisions made.
Of course, you can say that school-lunch status is a marker for race in a society where, sadly, economic and racial divisions line up closely. But at least people don’t explicitly choose a neighborhood based on the school-lunch status of the residents. The Schelling model seems to assume perfect information. Perhaps, when troubling social forces are in play, less than perfect information is a *good* thing.
My name is Denise Eckhardt and I am currently a student at West Chester University and for my public sphere class my partner Caitlin and I choose this topic as our collaborative group post. Below is the draft we have designed pertaining to the topic you are addressing.
Concerning Race Draft
This summer the Supreme Court heard two similar cases involving the problem of unintentional segregation in public schools. The two cases, one from Louisville and the other from Seattle, spoke of how schools have become one-sided in terms of race. This has happened naturally because of the neighborhoods that are included in school districts. Because of this phenomenon officials are trying to desegregate schools by considering race when deciding where to place children in public schools. The question is whether or not race should be a factor when deciding where children attend public schools.
Although we acknowledge that creating diversity can open opportunities, we believe that it can also limit access to better schools for kids originally in that school district because of different financial conditions in neighborhoods. Should we endanger children’s proper education for the sake of diverse classes? It is a well-known fact that some schools perform better then others when teaching children. If they have more funding and better teachers the students generally get a better education. Because of these varying levels of education, kids that live in a great school district may be assigned to a school district that is less than par. This can disrupt the child’s education process. Another question raised by these cases is whether or not students should have to travel to enjoy diversity. When students are reassigned to institutions outside their original school district, they may have to be bused far distances. It seems excessive to make the children get up earlier and travel farther just to create diversity in the classroom. Although we acknowledge that diversity is fundamental for education, we believe that diversity should not be created at the expense of the children because it could cause stress and problems for them and their parents.
Although we acknowledge that there are many different races in schools, we believe that their race should not be the determining factor when deciding where they attend school because of issues of reverse discrimination, violations of civil rights, and segregation. Anytime race is used as a factor in situations such as employment and education, it is not unusual for it to be labeled as “racist.” In several Supreme Court cases such as Grutter vs. Bollinger, the Supreme Court found the a Michigan Law school’s limited use of “affirmative action” constitutional but race is still a hot button issue especially in the growing area of “reverse discrimination.” (public.findlaw.com) Reverse discrimination is defined as the unfair treatment of members of majority groups resulting from preferential policies, as in college admissions or employment, intended to remedy earlier discrimination against minorities. In many cases, whites feel that they are losing privileges originally afforded to them due to public policies used to correct prior discrimination. In some cases affirmative actions and other programs that take race into account do result in reverse discrimination but not always. We do not believe that this is the intention or the purpose of the initiative proposed in Louisville and Seattle.
There are some advantages to having diversity in the classroom. Children can be taught about different cultures, tolerance, and other people at an early age. They will learn to respect people for their own beliefs and not be ethnocentric. Another positive result from this plan would be that children from poorer neighborhoods would have the opportunity to attend a more decent school. These opportunities would be great to have, but they can be achieved in different ways than described in the Louisville and Seattle cases.
Although there is much debate over using race as a means to an end, that end being diversity, there is no question that diversity in the nation’s public schools is important and essential in the society we live in today. The opportunities presented and the potential such an initiative holds in destroying prejudices and enlightening young minds are boundless. However, that is not to say that there is not another way to reach that goal. The government and administrators of our nation’s schools need to correct the fundamental problems facing education in the county before trying to implement such measures. Merely creating diversity will not solve the problems found in our inner cities’ schools by merely sending a portion of its students to another school in order to create diversity. What will become of the students who are not moved is just as an important question as those who do. In either case, the Supreme Court must consider all of theses factors, as we surely hope it will, than merely deciding if such an act is unconstitutional.