I often use a computer to create graphics, but there was a time when I used graphics to compute. That era came back to me the other day in the library. I was browsing among dusty volumes in the folio section when I came upon this:
The Design of Diagrams
for Engineering Formulas
and
The Theory of Nomography
by
Laurence I. Hewes, B. Sc., Ph. D.
and
Herbert L. Seward, Ph. B., M. E.
McGraw-Hill Book Company, Inc.
1923
The clerk at the circulation desk observed that there was no record anyone had ever borrowed this book. Although the records don’t go all the way back to 1923, I wouldn’t be surprised if I’m the first reader of this volume in 30 or 40 years.
It’s a book full of nomograms and similar graphic devices, with instructions on how to create them. Here’s a simple example for calculating the volume of a torus:
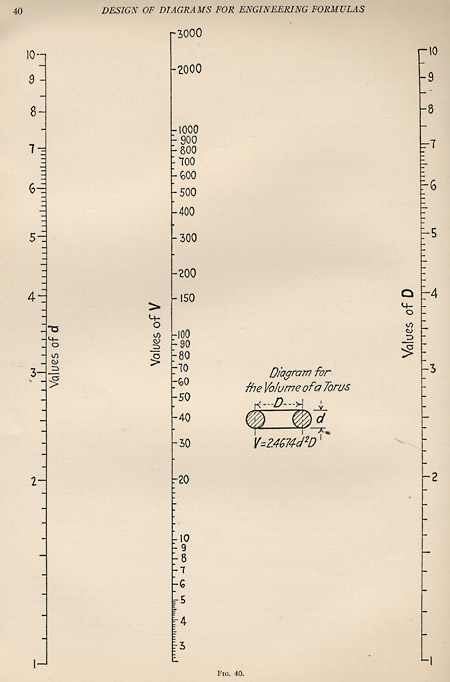
If you know any two of d, V and D, you can find the third quantity by laying a straightedge across the scales. (Quick quiz: What’s that constant in the formula V = 2.4674d2D?)
I used to see computational aids like this all the time. Some magazine I read in the seventies (I’m not sure which one—maybe Electronics?) published a new nomogram every month. But now such diagrams have a decidedly fusty look. They’re like tools you might find in an old blacksmith shop or a tannery; it’s a challenge just to figure out how they worked and what they were used for. You find yourself admiring the workers who created useful products with such implements.
The graphic device below is for calculating the strength of a metal plate pierced by rivet holes:
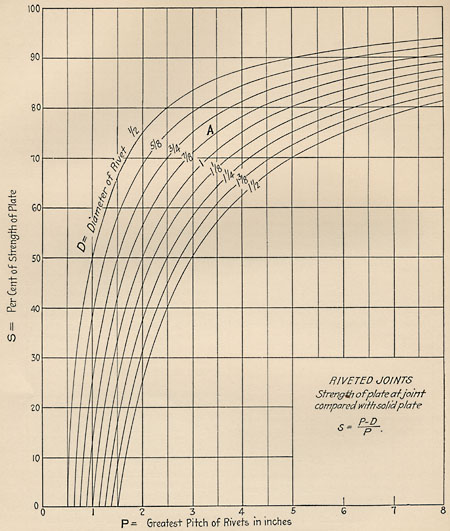
Did the engineers who specified the half-inch gusset plates for certain joints on the I-35W bridge in Minneapolis rely on such aids? The preliminary report from the National Transportation Safety Board (.pdf) doesn’t comment on the computational methods that might have been used when the bridge was designed in the early 1960s. In any case, it’s not at all obvious which is more error-prone—pencil and paper, slide rule, nomogram, CAD software.
The Theory of Nomography—as Hewes and Seward term their art—could hardly be more distant from modern computing practice. For one thing, it converts arithmetic into geometry; nowadays, we’re more likely to go the opposite way. A nomogram also emphasizes a static, declarative style of representing knowledge: A single diagram embodies all the relations of several variables, and one method solves for any unknown. Most digital computing is procedural rather than declarative; the emphasis is on step-by-step algorithms to go from givens to answers.
I’m not about to give up silicon in favor of paper computers, but I do find some of these diagrams both beautiful and illuminating. Here’s a nomogram for solving the quadratic equation z2+pz+q=0:
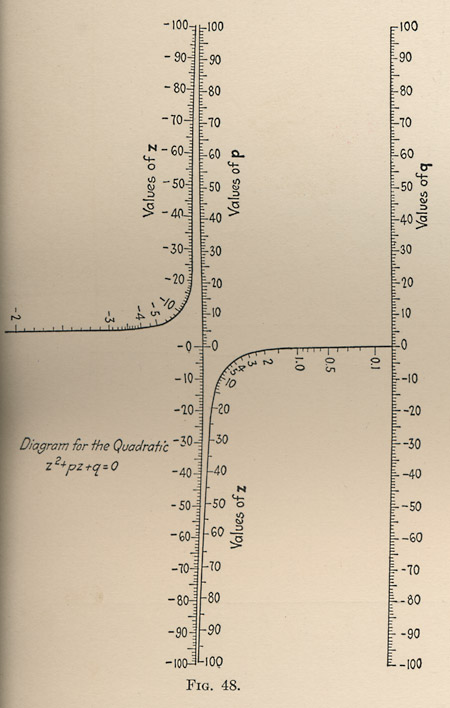
Instead of three straight-line scales, as in the formula for the volume of a torus, we have two linear scales and a hyperbola. A moment’s thought reveals why the diagram must have this form: For any combination of the coefficients p and q, the equation must have either two roots or no (real) root. One branch of the hyperbola carries all the positive roots and the other all the negative values of z. Poking around in the diagram brings various properties of the equation into sharp focus. For example, if you lay a straightedge across the diagram in such a way that it passes through the point p=0, then it will either cut the two branches of the hyperbola symmetrically (if q is negative) or it will miss both branches (if q is positive). This is no surprise—the roots of z2+q=0 had better be plus and minus the square root of q—but the graphic presentation carries a lot of explanatory force.
Hewes and Seward give an even more elaborate tableau for solving a cubic equation:
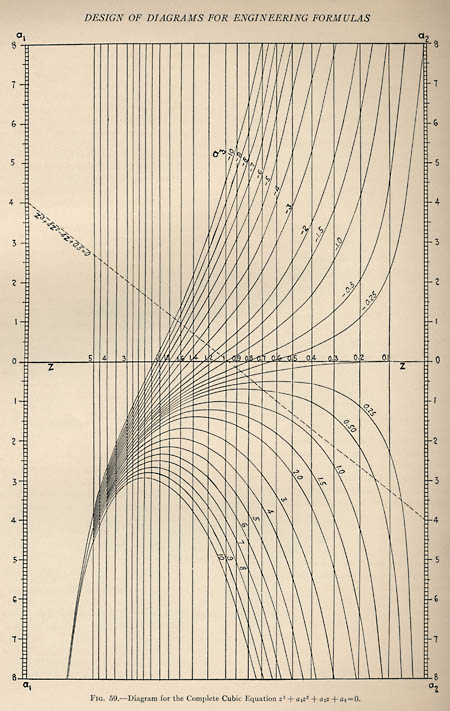
The dashed line drawn across this diagram represents a straightedge placed so as to solve the particular instance z3+4z2-4z+0.5=0. The straightedge is set to the points 4 and –4 on the left and right scales, and then the roots are read off by projecting vertically from the intersections of this line with the curve labeled 0.50. Working by eye, the roots appear to lie at about 0.15 and 0.7. Newton’s method—the archetype of iterative, step-by-step computations—gives 0.14758497342482376768480 and 0.69902089681305967783231. (On the SAGE server at the University of Washington, finding each of those roots took a couple of hundredths of a second.)
Note: Ask Dr. Math has an informative article on nomograms (or nomographs) with lots of references. One of the references led me to a 1999 lecture by Thomas Hankins, published in Isis (Hankins, Thomas L. 1999. Blood, dirt, and nomograms: A particular history of graphs. Isis 90(1):50–80). Hankins traces the origin and early history of the nomogram, which I had never known. Both the name and the concept came from Maurice d’Ocagne of the École des Ponts et Chaussées in Paris toward the end of the 19th century. Their first uses were in calculations needed for railroad construction.
Update 2008-03-05: Ron Doerfler, in a blog called Dead Reckonings, has several illuminating and thorough essays on the construction of nomographs, including a very fishy example laid out on an elliptic curve. The rest of the blog is also worth reading. Thanks to Mitch Burrill for the pointer.