I’m in Pittsburgh this weekend, attending a conference at Carnegie Mellon University. The sessions are being held in the Rashid Auditorium of the Gates Building.
The seats in the auditorium are upholstered with a pattern that seems apt for a computer science department, but it also begs for elucidation:
What is the patterning principle in these bits?
I’ve asked half a dozen people in the department—faculty, grad students, staff—but they all profess ignorance. Perhaps it’s a secret that’s never divulged to outsiders.
A quick web search turned up only one pertinent reference—a publication of the CMU chapter of the ACM. A photo caption on the last page includes this remark:
Do the binary codes written on the seats in Rashid Auditorium mean anything? After further investigation, we have concluded that while the binary patterns seem not to repeat, they do not map to any meaningful ASCII words.
Could it be true that the sequence has no repetition anywhere in the auditorium? I guess that depends on what you mean by repetition. Obviously short subsequences are repeated, and Axel Thue proved a century ago that no binary sequence can go on indefinitely without repeating some block of bits. But I have not tried to survey all 247 seats looking for the longest repeated block. (Most of the seats are occupied at the moment.)
I have a sneaking suspicion about what lies behind this pattern, but I’m trying to pay attention to a series of talks as I write this, so I’m not going to investigate further until I get home. In the meantime, I thought I’d throw open the question to anyone else who wants to speculate. To make the job a little easier, I’ve transcribed a few hundred bits:
1 0 1 0 1 1 0 1 1 1 0 1 0 1 0 0 0 1 1 0 1 1 0 1 0 1 1 0 1 1 1 0 1 0 1 0 1 0 0 0 1 0 1 0 1 1 0 1 0 1 0 0 0 1 1 0 1 1 0 0 1 0 1 0 1 1 0 1 1 1 0 1 0 1 0 0 0 1 1 1 0 1 0 0 1 1 1 0 1 1 0 1 0 1 0 1 1 0 1 1 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 1 0 1 0 1 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 1 1 0 1 1 0 1 0 0 1 1 1 0 1 1 0 1 0 1 0 1 1 0 1 0 1 1 0 1 0 1 0 0 1 1 0 1 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 1 0 0 1 0 1 0 1 1 1 0 0 1 1 0 1 0 1 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 1 0 0 1 1 0 1 0 1 0 0 1 0 1 0 1 0 0 1 1 1 0 1 0 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 1 0 1 1 1 0 1 0 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 1 0 0 1 1 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 1 0 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0 1 1 1 0 1 0 0 0 1 1 0 1 0 1 0 1 0 1 1 0 0 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 1 1 1 0 1 0 1 1 0 1 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 1 0 1 0 1 0 0 1 1 1 0 1 0 1 1 0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 0 0 1 0 1 0 0 1 0 1 0 1 1 0 1 1 1 0 1 0 1 0 0 0 1 1 1 1 1 0 1 0 1 1 0 1 1 0 0 1 0 1 0 1 1 0 1 1 1 0 1 1 1 0 1 0 1 0 1 0 0 0 1 0 1 0 0 1 0 1 0 1 1 1 1 0 1 1 0 1 0 1 0 0 0 1 1 0 1 0 0 1 1 1 0 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 0 1 1 0 1 0 1 1 0 1 0 0 1 1 1 0 1 1 0 1 0 1 1 1 0 1 1 0 1 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 0 1 0 1 0 1 1 1 0 1 0 1 1 0 1 0 1 0 0 1 1 0 1 0 1 0 0 0 1 1 0 1 0 0 1 0 0 0 1 1 0 1 0 1 1 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 1 1 0 1 0 1 1 0 1 0 1 0 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 0 1 1 1 0 1 0 1 0 1 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 1 1 1 0 1 0 1 1 1 0 1 0 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 1 1 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 1 0 1 0 1 1 0 1 0 1 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 1 0 1 1
Any ideas?
Update 2011-04-12: The “sneaking suspicion” I had in mind the other day was ridiculously wrong. I had wanted the pattern to be a segment of the Thue-Morse sequence, which I obliquely alluded to above. (Obliquely and also clumsily, as one commenter rightly pointed out.) The Thue-Morse sequence is one of the little gems of discrete mathematics, and it seemed like a perfect choice for a temple of high nerdiness like the CMU CS department. Here’s how the sequence begins:
0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1
At first glance—just taking in the optical texture of 1s and 0s—it seemed a good match for the fabric in Rashid Auditorium. But a closer look at the pattern on the chairs shows that the bits there cannot possibly be drawn from the Thue-Morse sequence. The key property of the sequence is that it is “cube-free”: No block of bits w is repeated three times in succession, as in www. The block w can be of any length, including a length of just one bit. The fabric pattern includes subsequences of 000 and 111, both of which violate the cube-free constraint. (I should have noticed this before I even got up out of my seat, but I didn’t.)
If not Thue-Morse, then what?
Several commenters note that it cannot simply be bits chosen uniformly at random, and I totally agree. Here are the frequencies of subsequences from one to four bits long:
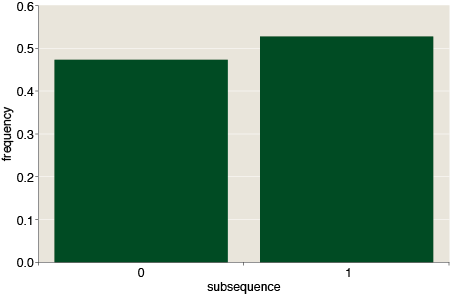
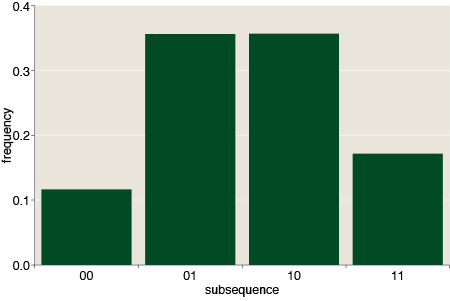
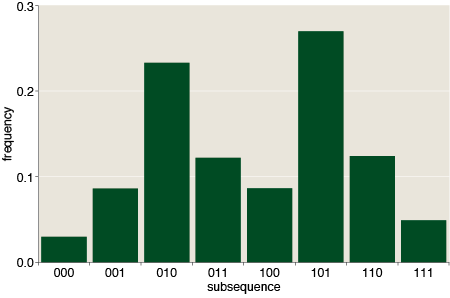
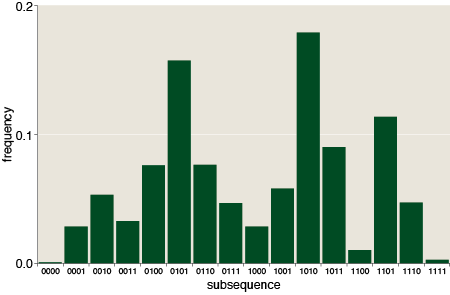
For random bits, all of these distributions are flat: Each k-bit subsequence occurs with expected frequency 2–k. The pattern at CMU is anything but flat. It has prominent peaks and valleys, with a notable excess of alternating 1s and 0s, and a corresponding deficit of subsequences that repeat the same symbol.
Another way to look at the bit sequences is through the autocorrelation function, which measures how well the sequence matches up with itself when shifted along its length by some fixed distance. An autocorrelation of 1.0 indicates a perfect match, and –1.0 is perfect anticorrelation—all the bits are different. For any series, the autocorrelation has to be 1.0 at a shift of 0. As the graph below shows, the autocorrelation function for the Rashid sequence is strongly negative at a shift of 1, and positive at shift 2. These results are consistent with the observed prevalence of alternating bits. Interestingly, the correlations continue to oscillate at larger shifts, with little sign of damping. What’s even more curious, for shifts greater than 4, the sign of the correlation is the opposite of what you’ve expect for an alternating 01 sequence.
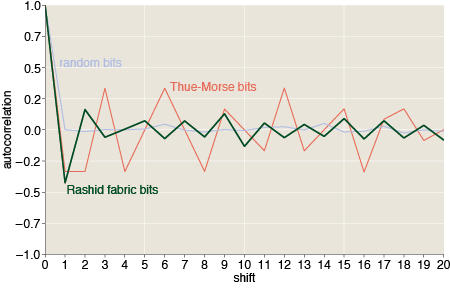
For comparison, the graph also shows the autocorrelation function of the Thue-Morse sequence, which has a fascinating structure of its own, and that of a random sequence of bits. Except at shift 0, the random sequence should converge on 0 autocorrelation everywhere.
The results above are based on a somewhat larger sample than the one I gave on Sunday. When I got home from Pittsburgh, I transcribed 35 rows of 79 digits each, for a total of 2,765 bits. I’ve treated the rows as 35 independent samples, since I don’t know how to join them without creating spurious conjunctions.
If you’d like to play with the bits for yourself, they are all here in a PDF that includes both an image of the fabric and my transcription of it. I should mention that typing 2,765 binary digits is not a lot of fun. Before embarking on that project, I struggled to get useful output from OCR services such as Online OCR, but the character-recognition algorithms try desperately to turn numerical data into English, producing stuff like this:
LOLOL010101.11.0110101.1.1010001010111.01.LoLotootoLoc t tot totot IMO /0t 100101 L LO LOLOt L tO1O 101000 OIOtOOlOLOtOlttOttOtOlttOOlOLOttOC
LOL indeed.
At this point, I admit I’m stumped. I just don’t know where all those bits came from.
The CMU-ACM magazine I mention above says the bit stream is not ASCII text. I don’t know how the author determined that, but I tend to agree. ASCII and most other byte-oriented encodings would show an autocorrelation spike at a shift of 8, and there’s no evidence of that.
I’m also sure the sequence is not Morse code. When you smush together letters and words in dot-dash encoding, the result has many more long runs than we see here.
Could it be the binary object code for some program? Rick Rashid was the principal author of the Mach operating system, created at CMU, so a fitting tribute would be to sew his work into the seats of the auditorium he funded. But I’ve never seen a core dump that looked anything like this. Most machine code has blocks of highly repetitive bit patterns.
Maybe the underlying message is text or an image that’s been run through a compression algorithm, such as gzip? That would raise the entropy of the signal and flatten the distribution of subsequences to some extent. But would it yield the specific pattern we see here? In particular, would it favor alternation of 0s and 1s? I don’t see why.
In the comments, Zvika suggests that the sequence looks like the product of a human operator trying to type randomly. I resist this idea. It’s just such an inhuman waste of human resources; I can’t stand to think of some poor schlub pecking away at a keyboard for hours, struggling to be mindless about it. But I suppose it could be true.
I came up with a slightly less barbaric alternative scenario. Suppose a fabric designer says to his programmer friend, “I need some random bits. Can you help me out?” The programmer goes away and fires up her RNG, and comes back with a million bits that pass all the usual tests of randomness. The designer says thanks, but later he complains, “These bits don’t look random. They’ve got all these long runs of 0s and 1s.” The programmer explains about independent choices from a uniform distribution, and the 1/2k spectrum of run lengths, but the designer will have none of it. “I don’t care about the math; give me something that looks right,” he says. So the programmer goes away and creates some new bits, meant to satisfy people who believe that when a coin has come up heads three times in a row, it’s more likely to show tails on the next toss.
I made an attempt to create such a function myself. It’s a simple Markov process, in which each appearance of a 1 in the sequence reduces the probability p that the next symbol will also be a 1. Specifically, I start with p = 1/2. If the next bit is a 1, p is adjusted to p/k, where k is a constant greater than 1. If the new bit is instead a 0, p becomes 1 — p/k. When I set k = 2, this process generated a stream of bits that looked much like the fabric pattern. Here’s a small sample:
1 0 1 1 0 1 0 1 1 0 1 0 0 1 0 1 1 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 1 0 1 1 1 1 0 1 0 1 0 1 1 0 1 0 1 0 1 1 1 1 0 1 1 0 1
And the subsequence frequencies also seemed broadly similar to those of the Rashid sequence:
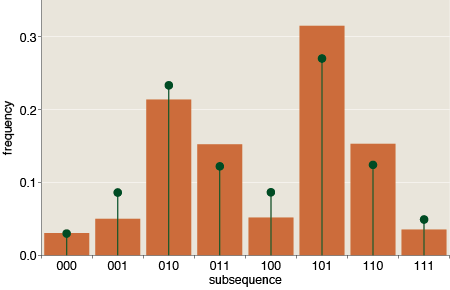
(The orange bars are the results for the Markov process; the green lollipops show the corresponding frequencies for the Rashid bits.) This outcome was at least mildly encouraging, but then I looked at the autocorrelations in the Markov-generated stream of bits:
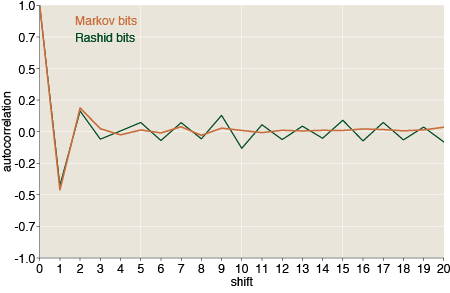
At shifts of 1 and 2, the Markov autocorrelations match those of the Rashid sequence almost exactly, but at longer distances the Markov correlations fade away, as they must in any random process. The long-range structure in the Rashid sequence seems all the more peculiar when displayed in this context.
Still another question is whether the fabric pattern can be truly aperiodic at large scales. If it were a printed fabric, I would be highly skeptical of this proposition. The printing process is inherently repetitive, with the same pattern recurring at intervals determined by the size of the printing plate or cylinder. (Think of wallpaper patterns.) But
the pattern on the upholstery cloth is not printed; it is woven into the fibers, and that changes everything. Looms have been programmable since the time of Jacquard, and there is no fundamental reason a modern loom could not be driven by a computer that supplies an arbitrarily long sequence of nonrepetitive instructions. The Thue-Morse sequence would do nicely for this purpose. So I can easily imagine an aperiodic upholstery pattern; I just don’t know if that’s what we’re seeing here.
Later this week I’ll go take a look at the Harvard version. (Thanks to Max Lin for discovering this second instance.)
Update 2011-04-13: I note here for the benefit of those who don’t read the comments: rouli has swept away all this speculation about looms driven by computers generating infinite aperiodic sequences. In the section of the pattern I transcribed, the last nine lines are identical to the first nine. I’ve checked a couple of other photos (of other seat backs) and confirmed that the whole pattern appears to repeat on a cycle of 26 lines.
How appalling that I could type more than 700 repeated characters and never notice the resemblance.
Update 2011-04-13, later:Yikes! And now Barry Cipra reveals that the pattern also repeats horizontally, with period 60.