Approximately Yours
by Brian Hayes
Published 22 July 2017
Today, I’m told, is Rational Approximation Day. It’s 22/7 (for those who write dates in little-endian format), which differs from π by about 0.04 percent. (The big-endians among us are welcome to approximate 1/π.)
Given the present state of life in America, what we really need is an Approximation to Rationality Day, but that may have to wait for 20/1/21. In the meantime, let us merrily fiddle with numbers, searching for ratios of integers that brazenly invade the personal space of famous irrationals.
When I was a teenager, somebody told me about the number 355/113, which is an exceptionally good approximation to π. “Somebody” was probably Martin Gardner, who mentioned the fraction in a 1965 Mathematical Games column. (Note added 5 May 2025.) The exact value is
3.141592920353982520964564173482358455657958984375,
correct through the first six digits after the decimal point. In other words, it differs from the true value by less than one-millionth. I was intrigued, and so I set out to find an even better approximation. My search was necessarily a pencil-and-paper affair, since I had no access to any electronic or even mechanical aids to computation. The spiral-bound notebook in which I made my calculations has not survived, and I remember nothing about the outcome of the effort.
A dozen years later I acquired some computing machinery: a Hewlett-Packard programmable calculator, called the HP-41C. Here is the main loop of an HP-41C program that searches for good rational approximations. Note the date at the top of the printout (written in middle-endian format). Apparently I was finishing up this program just before Approximation Day in 1981.

What’s that you say? You’re not fluent in the 30-year-old Hewlett-Packard dialect of reverse Polish notation? All right, here’s a program that does roughly the same thing, written in an oh-so-modern language, Julia.
function approximate(T, dmax)
d = 1
leastError = T
while d <= dmax && leastError > 0
n = Int(round(d * T))
err = abs(T - n/d) / T
merit = 1 / ((n + d)^2 * err)
if err < leastError
println("$n/$d = $(n/d) error = $err merit = $merit")
leastError = err
end
d += 1
end
endThe algorithm is a naive, sequential search for fractions \(n/d\) that approximate the target number \(T\). For each value of \(d\), you need to consider only one value of \(n\), namely the integer nearest to \(d \times T\). (What happens if \(d \times T\) falls halfway between two integers? That can’t happen if \(T\) is irrational.) Thus you can begin with \(d = 1\) and continue up to a specified largest denominator \(d = dmax\). The accuracy of the approximation is measured by the error term \(|T - n/d| / T\). Whenever a value of \(n/d\) yields a new minimum error, the program prints a line of results. (This version of the algorithm works correctly only for \(T \gt 1\), but it can readily be adapted to \(T \lt 1\).)
The HP-41C has a numerical precision of 10 decimal digits, and so the closest possible approximation to π is 3.141592654. Back in 1981 I ran the program until it found a fraction equal to this value—a perfect approximation, from the program’s point of view. According to a note on the printout, that took 13 hours. The Julia program above, running on a laptop, completes the same computation in about three milliseconds. You’re welcome to take a scroll through the results, below. (The numbers are not digit-for-digit identical to those generated by the HP-41C because Julia calculates with higher precision, about 16 decimal digits.)
3/1 = 3.0 error = 0.045070341573315915 merit = 1.3867212410256813
13/4 = 3.25 error = 0.03450712996224109 merit = 0.10027514940370374
16/5 = 3.2 error = 0.018591635655129744 merit = 0.12196741256165179
19/6 = 3.1666666666666665 error = 0.007981306117055373 merit = 0.20046844169789904
22/7 = 3.142857142857143 error = 0.0004024993041452083 merit = 2.9541930379680195
179/57 = 3.1403508771929824 error = 0.00039526983405584675 merit = 0.04542368072920613
201/64 = 3.140625 error = 0.0003080138345651019 merit = 0.04623150469956595
223/71 = 3.140845070422535 error = 0.00023796324342470652 merit = 0.04861781754719378
245/78 = 3.141025641025641 error = 0.0001804858353094197 merit = 0.053107007660473673
267/85 = 3.1411764705882352 error = 0.00013247529441315622 merit = 0.060922789404334425
289/92 = 3.141304347826087 error = 9.177070539240495e-5 merit = 0.07506646742266793
311/99 = 3.1414141414141414 error = 5.6822320879624425e-5 merit = 0.10469195703580983
333/106 = 3.141509433962264 error = 2.6489760736525772e-5 merit = 0.19588127575835135
355/113 = 3.1415929203539825 error = 8.478310581938076e-8 merit = 53.85164473263654
52518/16717 = 3.1415923909792425 error = 8.37221074104896e-8 merit = 0.00249177288308447
52873/16830 = 3.141592394533571 error = 8.259072954625822e-8 merit = 0.0024921016732136797
53228/16943 = 3.1415923980404887 error = 8.147444291923546e-8 merit = 0.0024926612882136163
53583/17056 = 3.141592401500938 error = 8.03729477091334e-8 merit = 0.0024934520351304946
53938/17169 = 3.1415924049158366 error = 7.928595172899531e-8 merit = 0.0024944743578840687
54293/17282 = 3.141592408286078 error = 7.821317056655376e-8 merit = 0.0024957288257085445
54648/17395 = 3.141592411612532 error = 7.715432730151448e-8 merit = 0.002497216134767719
55003/17508 = 3.1415924148960475 error = 7.610915194012454e-8 merit = 0.0024989371196291283
55358/17621 = 3.1415924181374497 error = 7.507738155653036e-8 merit = 0.0025008927426067996
55713/17734 = 3.1415924213375437 error = 7.405876001006156e-8 merit = 0.0025030840968725283
56068/17847 = 3.1415924244971145 error = 7.305303737979925e-8 merit = 0.002505512419906649
56423/17960 = 3.1415924276169265 error = 7.20599703886498e-8 merit = 0.002508179074048983
56778/18073 = 3.141592430697726 error = 7.107932141383905e-8 merit = 0.0025110855755419263
57133/18186 = 3.14159243374024 error = 7.01108591937022e-8 merit = 0.002514233565685482
57488/18299 = 3.1415924367451775 error = 6.915435783817789e-8 merit = 0.0025176248413626597
57843/18412 = 3.1415924397132304 error = 6.820959725288218e-8 merit = 0.0025212613363967255
58198/18525 = 3.141592442645074 error = 6.727636243231866e-8 merit = 0.002525145143834103
58553/18638 = 3.141592445541367 error = 6.635444374259433e-8 merit = 0.0025292785028112976
58908/18751 = 3.141592448402752 error = 6.544363663870371e-8 merit = 0.0025336638062423296
59263/18864 = 3.141592451229856 error = 6.454374152317083e-8 merit = 0.002538303603848205
59618/18977 = 3.1415924540232916 error = 6.365456332197522e-8 merit = 0.002543200616913158
59973/19090 = 3.1415924567836564 error = 6.277591190862598e-8 merit = 0.002548357720152209
60328/19203 = 3.1415924595115348 error = 6.190760125601375e-8 merit = 0.0025537779743748956
60683/19316 = 3.1415924622074964 error = 6.10494500018427e-8 merit = 0.0025594646031786867
61038/19429 = 3.1415924648720983 error = 6.020128088319864e-8 merit = 0.002565421015548036
61393/19542 = 3.141592467505885 error = 5.936292059519092e-8 merit = 0.0025716508123781218
61748/19655 = 3.141592470109387 error = 5.853420007366852e-8 merit = 0.0025781577749599853
62103/19768 = 3.1415924726831244 error = 5.771495407114599e-8 merit = 0.002584945883912429
62458/19881 = 3.141592475227604 error = 5.690502101544554e-8 merit = 0.002592019327133724
62813/19994 = 3.141592477743323 error = 5.6104242868339024e-8 merit = 0.0025993825084809985
63168/20107 = 3.1415924802307655 error = 5.531246526690591e-8 merit = 0.0026070400439016164
63523/20220 = 3.1415924826904056 error = 5.4529537523533324e-8 merit = 0.0026149967637792084
63878/20333 = 3.141592485122707 error = 5.375531191912607e-8 merit = 0.002623257749852838
64233/20446 = 3.141592487528123 error = 5.2989644268538606e-8 merit = 0.0026318283126966317
64588/20559 = 3.141592489907097 error = 5.22323933551431e-8 merit = 0.0026407140236596287
64943/20672 = 3.1415924922600618 error = 5.148342135490336e-8 merit = 0.002649920699086574
65298/20785 = 3.1415924945874427 error = 5.0742592988226976e-8 merit = 0.002659454449139831
65653/20898 = 3.1415924968896545 error = 5.0009776226755164e-8 merit = 0.0026693216486930156
66008/21011 = 3.141592499167103 error = 4.928484186928889e-8 merit = 0.002679528965991537
66363/21124 = 3.1415925014201855 error = 4.8567663400430846e-8 merit = 0.0026900833784673454
66718/21237 = 3.1415925036492913 error = 4.7858116990585446e-8 merit = 0.0027009921818650063
67073/21350 = 3.141592505854801 error = 4.715608149595883e-8 merit = 0.0027122629998437182
67428/21463 = 3.1415925080370872 error = 4.6461438175842924e-8 merit = 0.002723903810648984
67783/21576 = 3.1415925101965145 error = 4.577407111668933e-8 merit = 0.002735922933992634
68138/21689 = 3.1415925123334407 error = 4.5093866383961494e-8 merit = 0.0027483290931549346
68493/21802 = 3.1415925144482157 error = 4.442071258756658e-8 merit = 0.002761131395876878
68848/21915 = 3.141592516541182 error = 4.375450074049751e-8 merit = 0.002774339356802981
69203/22028 = 3.1415925186126747 error = 4.309512411747499e-8 merit = 0.0027879629217230834
69558/22141 = 3.1415925206630235 error = 4.244247783087354e-8 merit = 0.002802012512429091
69913/22254 = 3.14159252269255 error = 4.179645953751142e-8 merit = 0.0028164989998024
70268/22367 = 3.1415925247015695 error = 4.115696873186072e-8 merit = 0.0028314337694556623
70623/22480 = 3.1415925266903915 error = 4.0523907028763286e-8 merit = 0.002846828724926181
70978/22593 = 3.141592528659319 error = 3.989717788071482e-8 merit = 0.00286269633032941
71333/22706 = 3.1415925306086496 error = 3.9276686719222797e-8 merit = 0.0028790496258831624
71688/22819 = 3.1415925325386738 error = 3.86623409548065e-8 merit = 0.0028959022542887716
72043/22932 = 3.141592534449677 error = 3.805404969428105e-8 merit = 0.0029132685103826087
72398/23045 = 3.1415925363419395 error = 3.7451723882115376e-8 merit = 0.0029311633622333107
72753/23158 = 3.1415925382157353 error = 3.685527615907423e-8 merit = 0.002949602495467867
73108/23271 = 3.1415925400713336 error = 3.626462086221821e-8 merit = 0.002968602349703417
73463/23384 = 3.1415925419089974 error = 3.567967430761971e-8 merit = 0.002988180133716996
73818/23497 = 3.141592543728987 error = 3.510035365949903e-8 merit = 0.003008353961046636
74173/23610 = 3.1415925455315543 error = 3.452657862652023e-8 merit = 0.003029142753805288
74528/23723 = 3.1415925473169497 error = 3.395826962413729e-8 merit = 0.0030505664465106676
74883/23836 = 3.141592549085417 error = 3.339534904681598e-8 merit = 0.0030726459300795604
75238/23949 = 3.1415925508371956 error = 3.283774056124397e-8 merit = 0.003095403169820992
75593/24062 = 3.141592552572521 error = 3.228536938904675e-8 merit = 0.0031188612412389144
75948/24175 = 3.1415925542916234 error = 3.173816202407169e-8 merit = 0.0031430444223940115
76303/24288 = 3.14159255599473 error = 3.1196046373746034e-8 merit = 0.0031679782521683033
76658/24401 = 3.141592557682062 error = 3.065895190043484e-8 merit = 0.0031936895918127546
77013/24514 = 3.1415925593538385 error = 3.01268089146511e-8 merit = 0.0032202067806171002
77368/24627 = 3.141592561010273 error = 2.9599549423203633e-8 merit = 0.003247559639023363
77723/24740 = 3.1415925626515766 error = 2.9077106281049175e-8 merit = 0.0032757796556622983
78078/24853 = 3.1415925642779543 error = 2.8559414180798277e-8 merit = 0.0033048999843237645
78433/24966 = 3.14159256588961 error = 2.804640823913544e-8 merit = 0.003334955716987436
78788/25079 = 3.1415925674867418 error = 2.753802541039899e-8 merit = 0.0033659838476231357
79143/25192 = 3.141592569069546 error = 2.703420321435919e-8 merit = 0.003398023556100075
79498/25305 = 3.1415925706382137 error = 2.6534880725724155e-8 merit = 0.0034311162371627422
79853/25418 = 3.141592572192934 error = 2.6039997867349902e-8 merit = 0.0034653057466538235
80208/25531 = 3.141592573733892 error = 2.554949569295635e-8 merit = 0.0035006385417218717
80563/25644 = 3.14159257526127 error = 2.5063316245769302e-8 merit = 0.0035371638899188347
80918/25757 = 3.1415925767752455 error = 2.4581402841236452e-8 merit = 0.0035749340371894456
81273/25870 = 3.1415925782759953 error = 2.410369936023742e-8 merit = 0.003614004535709633
81628/25983 = 3.1415925797636914 error = 2.3630150955873712e-8 merit = 0.00365443439340209
81983/26096 = 3.141592581238504 error = 2.3160703488036753e-8 merit = 0.00369628643041249
82338/26209 = 3.141592582700599 error = 2.2695304230197833e-8 merit = 0.003739627468693587
82693/26322 = 3.1415925841501404 error = 2.2233900879902193e-8 merit = 0.0037845288174018898
83048/26435 = 3.1415925855872895 error = 2.1776442124200985e-8 merit = 0.0038310665494126084
83403/26548 = 3.1415925870122043 error = 2.1322877639651253e-8 merit = 0.00387932189896066
83758/26661 = 3.1415925884250404 error = 2.087315795095796e-8 merit = 0.003929381726572982
84113/26774 = 3.1415925898259505 error = 2.0427234430973973e-8 merit = 0.003981339007706688
84468/26887 = 3.1415925912150855 error = 1.9985059017984126e-8 merit = 0.004035293430477111
84823/27000 = 3.1415925925925925 error = 1.9546584922495102e-8 merit = 0.004091351857390988
85178/27113 = 3.1415925939586176 error = 1.9111765637729565e-8 merit = 0.004149629190123568
85533/27226 = 3.1415925953133033 error = 1.868055578777407e-8 merit = 0.004210248941258058
85888/27339 = 3.141592596656791 error = 1.825291042078912e-8 merit = 0.004273344214343279
86243/27452 = 3.1415925979892174 error = 1.78287858571571e-8 merit = 0.004339058439193095
86598/27565 = 3.1415925993107203 error = 1.7408138417260385e-8 merit = 0.004407546707464268
86953/27678 = 3.1415926006214323 error = 1.6990925835061217e-8 merit = 0.004478976601684539
87308/27791 = 3.1415926019214853 error = 1.6577106127237806e-8 merit = 0.004553529781140699
87663/27904 = 3.1415926032110093 error = 1.6166637875900305e-8 merit = 0.004631403402447433
88018/28017 = 3.141592604490131 error = 1.5759480794022753e-8 merit = 0.0047128116308472546
88373/28130 = 3.141592605758976 error = 1.5355594877295166e-8 merit = 0.004797987771392931
88728/28243 = 3.1415926070176683 error = 1.4954940686839493e-8 merit = 0.0048871863549194705
89083/28356 = 3.141592608266328 error = 1.4557479914641577e-8 merit = 0.004980685405908598
89438/28469 = 3.141592609505076 error = 1.4163174252687263e-8 merit = 0.005078789613658918
89793/28582 = 3.1415926107340284 error = 1.3771986523826276e-8 merit = 0.005181833172630217
90148/28695 = 3.141592611953302 error = 1.338387969226633e-8 merit = 0.005290183824183623
90503/28808 = 3.1415926131630103 error = 1.2998817570363058e-8 merit = 0.005404246870669908
90858/28921 = 3.1415926143632653 error = 1.2616764535904027e-8 merit = 0.005524470210563737
91213/29034 = 3.141592615554178 error = 1.2237685249392783e-8 merit = 0.005651350205744754
91568/29147 = 3.1415926167358563 error = 1.1861545360838771e-8 merit = 0.005785438063205309
91923/29260 = 3.1415926179084073 error = 1.1488310802967408e-8 merit = 0.005927347979056494
92278/29373 = 3.141592619071937 error = 1.111794779122008e-8 merit = 0.006077766389438445
92633/29486 = 3.141592620226548 error = 1.0750423671902066e-8 merit = 0.006237462409303776
92988/29599 = 3.1415926213723435 error = 1.0385705649960649e-8 merit = 0.006407301439430316
93343/29712 = 3.1415926225094237 error = 1.0023761778491034e-8 merit = 0.00658826005755035
93698/29825 = 3.1415926236378877 error = 9.664560534662385e-9 merit = 0.006781444748602359
94053/29938 = 3.1415926247578327 error = 9.308070961075804e-9 merit = 0.006988114128701429
94408/30051 = 3.1415926258693556 error = 8.954262241690382e-9 merit = 0.007209706348604964
94763/30164 = 3.14159262697255 error = 8.603104549971112e-9 merit = 0.007447871540046976
95118/30277 = 3.14159262806751 error = 8.254567918024995e-9 merit = 0.007704513406469473
95473/30390 = 3.141592629154327 error = 7.90862336746494e-9 merit = 0.007981838717667477
95828/30503 = 3.1415926302330917 error = 7.565241919903853e-9 merit = 0.008282421184374838
96183/30616 = 3.1415926313038933 error = 7.224395162386583e-9 merit = 0.008609280341750632
96538/30729 = 3.1415926323668195 error = 6.8860552473899216e-9 merit = 0.008965982432171553
96893/30842 = 3.1415926334219573 error = 6.550194468748648e-9 merit = 0.009356770586561815
97248/30955 = 3.141592634469391 error = 6.216785968445456e-9 merit = 0.009786732283709331
97603/31068 = 3.1415926355092054 error = 5.885802747105052e-9 merit = 0.010262022067809991
97958/31181 = 3.1415926365414837 error = 5.557218370784088e-9 merit = 0.010790155391967196
98313/31294 = 3.1415926375663066 error = 5.231007112329143e-9 merit = 0.011380406450991833
98668/31407 = 3.1415926385837554 error = 4.907143103228812e-9 merit = 0.012044356667029002
99023/31520 = 3.1415926395939087 error = 4.585601323119603e-9 merit = 0.01279665696194468
99378/31633 = 3.141592640596845 error = 4.266356751638026e-9 merit = 0.013656119502875172
99733/31746 = 3.1415926415926414 error = 3.9493849338525334e-9 merit = 0.014647305857352692
100088/31859 = 3.141592642581374 error = 3.6346615561895634e-9 merit = 0.015802906908552822
100443/31972 = 3.1415926435631176 error = 3.322162870507497e-9 merit = 0.017167407267272748
100798/32085 = 3.1415926445379463 error = 3.0118652700227016e-9 merit = 0.018802933529623964
101153/32198 = 3.141592645505932 error = 2.703745854741474e-9 merit = 0.020798958087527405
101508/32311 = 3.1415926464671475 error = 2.397781441954139e-9 merit = 0.02328921472604781
101863/32424 = 3.141592647421663 error = 2.0939496970989362e-9 merit = 0.026482916558483883
102218/32537 = 3.1415926483695484 error = 1.7922284269720909e-9 merit = 0.03072676661447583
102573/32650 = 3.141592649310873 error = 1.492595579727815e-9 merit = 0.03664010548445531
102928/32763 = 3.141592650245704 error = 1.195029527594277e-9 merit = 0.04544847105306477
103283/32876 = 3.1415926511741086 error = 8.995092082315892e-10 merit = 0.05996553050516452
103638/32989 = 3.1415926520961532 error = 6.060132765838922e-10 merit = 0.0883984797913258
103993/33102 = 3.1415926530119025 error = 3.1452123574324146e-10 merit = 0.16916355170353897
104348/33215 = 3.141592653921421 error = 2.5012447443706518e-11 merit = 2.1127131430431656
The error values in the middle column of the table above shrink steadily as you read from the top of the list to the bottom. Each successive approximation is more accurate than all those above it. Does that also mean each successive approximation is better than those above it? I would say no. Any reasonable notion of “better” in this context has to take into account the size of the numerator and the denominator.
If you want an approximation of \(\pi\) accurate to seven digits, I can give you one off the top of my head: \(3141593/1000000\). But the numbers making up that ratio are themselves seven digits long. What makes \(355/113\) impressive is that it achieves seven-digit accuracy with only three digits in the numerator and the denominator. Accordingly, I would argue that a “better” approximation is one that minimizes both error and size. The rightmost column of the table, filled with numbers labeled “merit” is meant to quantify this intuition.
When I wrote that program in 1981, I chose a strange formula for merit, one that now baffles me:
\[\frac{1}{(n + d)^2 * err}.\]
Adding the numerator and denominator and then squaring the sum is an operation that makes no sense, although the formula as a whole does have the correct qualitative behavior, favoring both smaller errors and smaller values of \(n\) and \(d\). In trying to reconstruct what I had in mind 26 years ago, my best guess is that I was trying to capture a geometric insight, and I flubbed it when translating math into code. On this assumption, the correct figure of merit would be:
\[\frac{1}{\sqrt{n^2 + d^2} * err}.\]
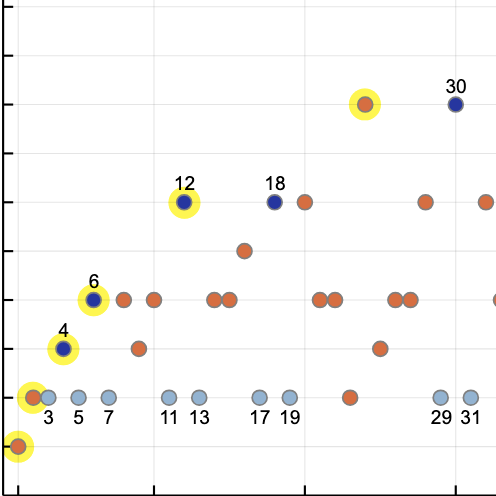
To see where this formula comes from, consider a two-dimensional lattice of integers, with a ray of slope \(\pi\) drawn from the origin and going on to infinite distance.

Because the line’s slope is irrational, it will never pass through any point of the integer lattice, but it will have many near misses. The near-miss points, with coordinates interpreted as numerator and denominator, are the accurate approximations to \(\pi\). The diagram suggests a measure of the merit based on distances. An approximation gets better when we minimize the distance of the lattice point from the origin as well as the vertical distance from the point to the \(\pi\) line. That’s the meaning of the formula with \(\sqrt{n^2 + d^2}\) in the denominator.
Another approach to defining merit simply counts digits. The merit is the ratio of the number of correctly predicted digits in the irrational target \(T\) to the number of digits in the denominator. A problem with this scheme is that it’s rather coarse. For example, \(13/4\) and \(16/5\) both have single-digit denominators and they each get one digit of \(\pi\) correct, but
\(16/5\) actually has a smaller error.
To smooth out the digit-counting criterion, and distinguish between values that differ in magnitude but have the same number of digits, we can take logarithms of the numbers. Let merit equal: \(-log(err) / log(d)\). (The \(log(err)\) term is negated because the error is always less than \(1\) and so its logarithm is negative.)
Here’s a comparison of the three merit criteria for some selected approximations to \(\pi\):
n/d 1981 merit distance merit log merit
3/1 1.3867212448620723 7.016316181613145 --
13/4 0.10027514901117529 2.1306165422053285 2.4284808488226544
16/5 0.12196741168912356 3.208700907602539 2.4760467349663537
19/6 0.20046843839209055 6.288264070960828 2.6960388788612515
22/7 2.954192079226498 107.61458138965322 4.017563128080901
179/57 0.04542369572848121 13.467303354323912 1.9381258641568968
201/64 0.04623152429195394 15.390920494844842 1.9441196398907357
223/71 0.04861784421796857 17.956388291625093 1.9573120958787444
245/78 0.05310704607396699 21.548988850935377 1.9785253787278367
267/85 0.06092284944437125 26.93965209372642 2.0098618723780515
289/92 0.07506657421887829 35.92841360228601 2.055872071177696
311/99 0.10469219759604646 53.921550739835986 2.1273838230139175
333/106 0.1958822412726219 108.02438852795403 2.259868093766371
355/113 53.76883630752973 31610.90993685001 3.444107245852723
52163/16604 0.002495514149618044 215.57611105028013 1.6757260012234105
• • • •
• • • •
• • • •
103993/33102 0.2892417579456485 49813.04849576935 2.1538978293241056
104348/33215 0.5006051667655171 86508.24042805366 2.2065386096084607
208341/66317 0.3403602724772912 117433.39822796892 2.1589243556399245
312689/99532 0.6343809166515098 328504.0552596196 2.207421489352196
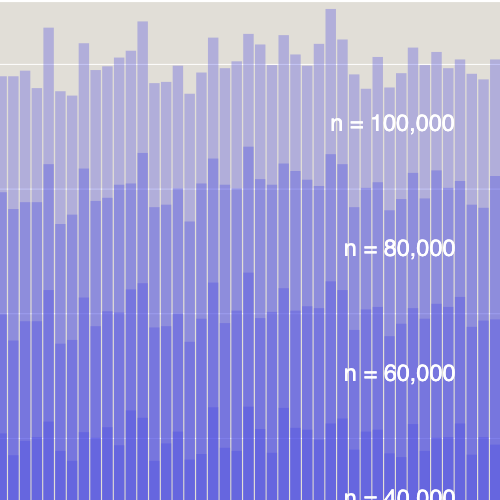
All three measures agree that \(22/7\) and \(355/113\) are quite special. In other respects they give quite different views of the data. My weird 1981 formula compares \((n + d)^{-2}\) with \(err^{-1}\); the asymmetry in the exponents suggests the merit will tend to zero as \(n\) and \(d\) increase, at least in the average case. The maximum of the distance-based measure, on the other hand, appears to grow without bound. And the logarithmic merit function seems to be settling on a value near 2.0. This implies that we shouldn’t expect to see many \(n/d \) approximations where the number of correct digits is greater than twice the number of digits in \(d\). The late Tom Apostol and Mamikon A. Mnatsakanian proved a closely related proposition (“Surprisingly accurate rational approximations,” Mathematics Magazine, Vol. 75, No. 4 (Oct. 2002), pp. 307-310).
The final joke on my 1981 self is that all this searching for better approximants can be neatly sidestepped by a bit of algorithmic sophistication. The magic phrase is “continued fractions.” The continued fraction for \(\pi\) begins:
\[ \pi = 3+\cfrac{1}{7+\cfrac{1}{15+\cfrac{1}{1+\cfrac{1}{292+\cfrac{1}{1 + \cdots}}}}}\]
Evaluating the successive levels of this expression yields a sequence of “convergents” that should look familiar:
\[3/1, 22/7, 333/106, 355/113, 103993/33102, 104348/33215.\]
It is a series of “best” approximations to \(\pi\), generated without bothering with all the intervening non-“best” values. I produced this list in CoCalc (a.k.a. SageMathCloud), following the excellent tutorial in William Stein’s Elementary Number Theory. Even much larger approximants gush forth from the algorithm in milliseconds. Here’s the 100th element of the series:
\[\frac{4170888101980193551139105407396069754167439670144501}{1327634917026642108692848192776111345311909093498260}\]
A question remains: In what sense are these approximations “best”? It’s guaranteed that every element of the series is more accurate than all those that came before, but it’s not clear to me that they also satisfy any sort of compactness criterion. But that’s a question to be taken up another day. Perhaps on Continued Fraction Day.
Correction (5 May 2025): The text above gives a decimal expansion for \(355/113\) that purports to be the “exact value” of the expression. It’s anything but. No finite sequence of digits could be the exact value of \(355/113\), because the quotient of those numbers is a repeating decimal with a period of 112 digits. The correct statement is:
where the vinculum, or overline, indicates that the entire 112-digit sequence repeats indefinitely.
The erroneous value I calculated in 2017 is not merely incomplete; it’s plain wrong. Every digit after the 15th decimal place is numerical noise.
Responses from readers:
Please note: The bit-player website is no longer equipped to accept and publish comments from readers, but the author is still eager to hear from you. Send comments, criticism, compliments, or corrections to brian@bit-player.org.
Publication history
First publication: 22 July 2017
Converted to Eleventy framework: 22 April 2025
Fix links, add note and correction: 5 May 2025


Hi Brian! What a fun story! Reading this, I thought you might enjoy a very closely-related post I wrote back when *I* was a kid, in which I calculated that \(1337^{47168026} \approx 3.1415926 \times 10^{147453447}\). The link is here if you’re curious.
P.S. May I include a link to this post on this month’s Aperiodical Carnival of Mathematics?
Terrific story! Thanks for letting me (and other readers here) know about it.
As for the Carnival — of course, I’d be delighted.
The Number Theory literature recognizes two different kinds of “best approximation” of a rational to an irrational. Following Joe Roberts’ text, Elementary Number Theory, a fraction which is closer to a real number x than every other fraction with equal or smaller denominator is called a best approximation of the first kind (BA1, for short) to x. Every convergent of the continued fraction for x is a BA1 to x.
If a, b are relatively prime positive integers, and if \(|bx-a|<|dx-c|\) for all pairs c, d of relatively prime positive integers satisfying \(d\le b\) and \(c/d\ne a/b\), then a/b is called a best approximation of the 2nd kind (BA2) to x. Every BA2 to x is a BA1 to x, but not conversely. A fraction is a BA2 to x if and only if it is a convergent of the continued fraction for x.
A theorem of Hurwitz states that for every real irrational x there are infinitely many rational approximations a/b with \(|bx-a|<(\sqrt5 b)^{-1}\). So if you use \(|bx-a|^{-1}\) as a measure of the merit of the approximation a/b, you'll find that every real irrational has a sequence of approximations of unbounded merit. If you use \((b|bx-a|)^{-1}\), you'll find that each quadratic irrational has only approximations of bounded merit. The precise behavior of \(\log|b\pi-a|/\log b\) as a/b runs through approximations to pi is not known.
Thanks very much for explaining so clearly.
In the statement of the Hurwitz theorem, should it be \((\sqrt{5}b^2)^{-1}\)?
The Hurwitz theorem is often stated as \(|x-(a/b)|<(\sqrt5b^2)^{-1}\), but I've multiplied through by b.
Aha. Thanks again.
I just noticed that you’re missing a partial quotient in the continued fraction for pi. There should be a 1 between the 15 and the 292.
Thanks! Fixed.
I missed this when it was posted, but regarding the question at the end (already answered by Gerry Myerson above), I wrote a bit about this a few years ago: https://shreevatsa.wordpress.com/2011/01/10/not-all-best-rational-approximations-are-the-convergents-of-the-continued-fraction/
Thanks for the link! Obviously I missed yours, too.