Mathematics is a tool for understanding the world we live in. Mathematics is also a world unto itself, detached from the material universe, a realm built not from matter and energy but from the stuff of imagination. In the mathematical universe we can not only explore but also create, inventing new geometries, new kinds of numbers, even new kinds of logic. Mathematics, in other words, can take you out of this world. Bertrand Russell, who charted the territory of mathematics a century ago, spoke of opening “windows into a larger and less fretful cosmos.”
Crinkly Curves
In 1877 the German mathematician Georg Cantor made a shocking discovery. He found that a two-dimensional surface contains no more points than a one-dimensional line. Intuition rebels against this notion. Inside a square you could draw infinitely many parallel line segments side by side. Surely an area with room for such an infinite array of lines must include more points than a single line—but it doesn’t. Cantor himself was incredulous: “I see it, but I don’t believe it,” he wrote.
Quasirandom Ramblings
Suppose you want to estimate the area of an object with a complicated shape, such as a maple leaf. There’s a well-known trick for solving this problem with the help of a little randomness. Put the leaf on a board of known area, then throw darts at it randomly, trying not to aim. If a total of N darts hit the board, and n of them land within the leaf, then the ratio n:N approximates the ratio of the leaf area to the board area.
How to Avoid Yourself
Every Sunday morning you go for a walk in the city, heading nowhere in particular, with just one rule to your rambling: You never retrace your steps or cross your own path. If you have already walked along a certain block or passed through an intersection, you refuse to set foot there again. This recipe for tracing a loopless path through a grid of city streets leads into some surprising back alleys of mathematics. Avoiding yourself, it turns out, is a hard problem.
First Links in the Markov Chain
It was an unlikely partnership of poetry and probability theory. Delving into the text of Alexander Pushkin’s novel-in-verse Eugene Onegin, the Russian mathematician A. A. Markov spent hours sifting through patterns of vowels and consonants. His analysis did not alter the understanding or appreciation of Pushkin’s poem, but the technique he developed—now known as a Markov chain—extended the theory of probability in a new direction. And it gave us a marvelous tool for turning literature into drivel.
Foolproof
I was a teenage angle trisector. In my first full-time job, fresh out of high school, I trisected angles for $1.75 an hour. My employer was a maker of voltmeters, ammeters, and other electrical instruments. This was in the analog age, when a meter had a slender pointer swinging in an arc across a scale. My job was drawing the scale, using ruler and compass and a fine pen. Often I would have to divide an angle into three equal parts—a trisection. I joked about this with my coworker. We should get extra pay, I said, for solving one of the most famous unsolvable problems of antiquity.
Foolproof is a collection of essays on mathematical themes. If the snippets above have piqued your interest, you might like the rest of the book too.
The essays explore mathematical ideas that provoke puzzlement and wonder: sets of numbers that have no average, higher-dimensional spaces where spheres shrink away to nothing, curves that are so twisty they cover every point on a plane, a gambling game that you can never win or lose or tie. A few of the essays look toward the research frontier, reporting on topics such as the distribution of prime numbers. Others are historical: A famous anecdote has young Carl Friedrich Gauss outfoxing his math teacher; did it really happen that way? The title essay explores the beautiful but sometimes treacherous idea of mathematical proof.
All of the chapters derive from essays that first appeared as “Computing Science” columns in American Scientist magazine; they have been corrected, revised, and updated for this volume. (Links to the original magazine versions are given in the table of contents below.)
Publication details
Foolproof, and Other Mathematical Meditations, by Brian Hayes. The MIT Press. September 2017.
Hardcover edition: ISBN 978-0-262-03686-3, $24.95.
Paperbound edition: ISBN 978-0-262-53607-3, $17.95.
eBook edition: ISBN 978-0-262-34267-4, $17.95.
Where to get it
Ask at your local bookstore.
Order from the publisher.
Order from Amazon.
See if a nearby library has a copy.
Contents
Chapter 1. Young Gauss Sums It Up
A schoolboy’s triumph over a harsh teacher becomes the stuff of legend
Chapter 2. Outside the Law of Averages
Not just above average but beyond the reach of all averages
Chapter 3. How to Avoid Yourself
Taking a walk without crossing your own path leads into curious byways
Chapter 4. The Spectrum of Riemannium
An unexpected connection between nuclear physics and prime numbers
Chapter 5. Unwed Numbers
In Sudoku “No math is required,” but there’s plenty behind the scenes
Chapter 6. Crinkly Curves
A scribbled line grows so twisty that it touches every point on a plane
Chapter 7. Wagering with Zeno
You can’t win, you can’t lose, you can’t tie, and the game never ends
Chapter 8. The Higher Arithmetic
New tools for doing arithmetic with enormous numbers
Chapter 9. First Links in the Markov Chain
A crucial innovation in probability began with an analysis of poetry
Chapter 10. Playing Ball in the nth Dimension
Spheres in a space of many dimensions seem to shrink away to nothing
Chapter 11. Quasirandom Ramblings
Somewhere between the chaotic and the orderly lies the quasirandom
Chapter 12. Pencil, Paper, and Pi
Forensic mathematics investigates a heroic computation that went awry
Chapter 13. Foolproof
Is proof a magic wand that works only in the hands of wizards?
About the author
Hello, I’m Brian Hayes. I write about science, mathematics, computation, and technology. In the 1970s and 80s I was an editor at Scientific American, and since 1990 I have been associated with American Scientist. The essays in Foolproof began life as columns in the latter magazine. I’ve also written and illustrated two other books, Infrastructure: A Guide to the Industrial Landscape (W. W. Norton, 2005, 2014) and Group Theory in the Bedroom, and Other Mathematical Diversions (Hill and Wang, 2008). My blog is called Bit-Player.
I am not a mathematician, just a writer who became enchanted with mathematical thinking. To put it another way, I have been an avid student of mathematics for more than 50 years, but I still have a lot to learn.
I live in North Carolina with my wife Rosalind Reid, who is also a science writer. I recently spent a semester in Berkeley, California, as Journalist in Residence at the Simons Institute for the Theory of Computing. I am proud to acknowledge a fellowship from Y Combinator Research, which provided support during the preparation of this book.
If you have questions or comments about Foolproof, please send me an email: brian@bit-player.org.
Nice words from my friends
“With a journalist’s instinct for story, a mathematician’s concern for accuracy, and a storryteller’s sense of narrative, Brian Hayes lets the general reader in on a secret mathematicians already know: math is fun! His vignettes are like the snapshots of a returned traveler, showing us exotic lands and the marvelous creatures that live there. Foolproof shows that the mathematical enterprise is one of high adventure.”
James Propp, Professor, University of Massachusetts Lowell
“Brian Hayes takes us with him as he roams far and wide across the mathematical landscape. Whether he’s braving the borderlands of the latest research or poking around in some forgotten corner of history, his chronicles of what he finds there are consistently captivating and revelatory.”
Steven Strogatz, Jacob Gould Sherman Professor of Applied Mathematics, Cornell University; author of The Joy of x
“Each of these essays brings unexpected twists of perception and presentation; what a fine imagination Hayes has! I enjoyed the book enormously.”
Nick Trefethen FRS, Professor of Numerical Analysis, University of Oxford; creator of Chebfun; author of Trefethen’s Index Cards
Reviews and Commentary
Dianne Timblin. Adventures in a Less Fretful Cosmos: A Conversation with Brian Hayes. American Scientist, September–October 2017, volume 105, pages 312–314. Online. PDF.
“Shecky Riemann”. Overview... Foolproof, and Other Mathematical Meditations. MathTango. October 8, 2017. Online. See also Books... Year-end Review. MathTango. November 24, 2017. Online.
Adhemar Bultheel. Review of Foolproof, and Other Mathematical Meditations. European Mathematical Society. October 27, 2017. Online.
Mark Hunacek. Review of Foolproof, and Other Mathematical Meditations. Mathematical Association of America. November 11, 2017. Online.
Brian Clegg. Review of Foolproof, and Other Mathematical Meditations. Popular Science: The popular science and science fiction book review site. November 19, 2017. Online.
Brian Clegg. Brian Hayes—Four-Way Interview. Popular Science: The popular science and science fiction book review site. November 26, 2017. Online.
Anna Haensch. Review of Foolproof, and Other Mathematical Meditations. Math Horizons 25(4):29, March, 2018. Online ($$). Another online source.
William Denton. Review of Foolproof, and Other Mathematical Meditations. Miskatonic University Press, 25 April 2018. Online.
Francesca Arici. Review (in Italian) of Foolproof, and Other Mathematical Meditations. Math Is in the Air, 16 September 2018. Online.
Updates and corrections
page 78: In Figure 5.3, which shows an array of 16 order-2 sudoku grids, the grid at the bottom right is not a valid sudoku solution, because two of the columns have repeated numbers. The corrected figure is shown below. The error was discovered and reported by Roger Luther, of Brighton, UK.
page 120, four lines from the bottom: “as it might see” should be “as it might seem”
page 182: In describing the errors that William Shanks made in calculating hundreds of digits of π, I made some mistake of my own, all too similar to his. Near the top of page 182, the number labeled U497 is incorrect. The line should read:
U497 0.000 ... 9074446680084838973843
This error was discovered by Haruyuki Kawabe, who is preparing a Japanese translation of Foolproof.
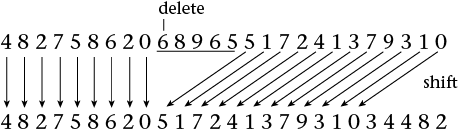
page 183: Another error pointed out by Haruyuki Kawabe. A diagram on page 183 shows how Shanks may have omitted five digits, probably while transcribing a value from one worksheet to another. Unfortunately, I marked the wrong five digits for deletion. Here is a corrected version of the diagram.
