The Mind Wanders
by Brian Hayes
Published 31 July 2018
On my walk to the Berkeley campus this morning I brushed my fingers through the leaves of an aromatic shrub, and then inhaled the familiar fragrance. I do this every day, and every day the first word that stands up and waves its arms around demanding my attention is sage. But I know the plant is not sage, it’s rosemary, so I tell sage to sit down. Too late. With rosemary and sage already front and center, I can’t stop parsley and thyme from sauntering onstage to join them, and then along come the first bars of the melody and the faces on the album cover, and I’m back in the middle of the 1960s wearing a paisley shirt. Meanwhile, rosemary evokes Rosemary Woods and the \(13\)-minute gap (though I now know, after consulting the global collective memory, that it’s Rose Mary Woods and the \(18\frac{1}{2}\)-minute gap). From Watergate I leap forward to stories on this morning’s front page. Then I notice another plant in a well-tended garden, with furry gray-green leaves. This one isn’t sage either; it’s lamb’s ear. Nevertheless, sage finally has its moment in the spotlight. From the herb I move on to the mathematical software called Sage, and then to SAGE, the Semi-Automatic Ground Environment, the 1950s air-defense system controlled by the largest computer ever built.
In psychology and literature, this kind of mental rambling is called stream of consciousness, a metaphor we owe to William James. It’s not the metaphor I would have chosen. My own consciousness, as I experience it, does not flow smoothly from one topic to the next but seems to flit across a landscape of ideas, more like a butterfly than a river, sometimes alighting daintily on one flower and then the next, sometimes carried away by gusts of wind, sometimes revisiting favorite spots over and over.
As a way of probing the architecture of my own memory, I have tried a more deliberate experiment in free association. I began with the same herbal recipe—parsley, sage, rosemary, and thyme—but for this exercise I wasn’t strolling through the garden spots of the Berkeley hills; I was sitting at a desk taking notes. The diagram below is my best effort at reconstructing the complete train of thought.
Scrolling through the chart from top to bottom reveals the items in the order my brain presented them to me, but the linkages between nodes do not form a single linear sequence. Instead the structure is treelike, with short chains of sequential associations ending with an abrupt return to an earlier node, as if I were being snapped back by a rubber band. These interruptions are marked in the diagram by green upward arrows; the red “X” at the bottom is where I decided to end the experiment.
My apologies to the half of humanity born since 1990, who will doubtless find many of the items mentioned in the diagram antiquated or obscure. You can hover over the labels for pop-up explanations, although I doubt they will make the associations any more meaningful. Memories, after all, are personal; they live inside your head. If you want a collection of ideas that resonate with your own experience, you’ll just have to create your own free-association diagram. I highly recommend it: You may discover something you didn’t know you knew.
The destination of my daily walk down the hill in Berkeley is the Simons Institute for the Theory of Computing, where I am immersed in a semester-long program on the Brain and Computation. It’s an environment that inspires thoughts about thoughts. I begin to wonder: What would it take to build a computational model of the free-association process? Among the various challenges proposed for artificial intelligence, this one looks easy. There’s no need for deep ratiocination; what we are asked to simulate is just woolgathering or daydreaming—what the mind does when it’s out of gear and the engine is idling. It ought to be effortless, no?
For the design of such a computational model, the first idea that comes to mind (at least to my mind) is a random walk on a mathematical graph, or network. The nodes of the network are things stored in memory—ideas, facts, events—and the links are various kinds of associations between them. For example, a node labeled butterfly might have links to moth, caterpillar, monarch, and frittillary, as well as the translations mentioned in the diagram above, and perhaps some less obvious connections, such as Australian crawl, shrimp, Muhammad Ali, pellagra, throttle valve, and stage fright. The data structure for a node of the network would include a list of pointers to all of these associated nodes. The pointers could be numbered from \(1\) to \(n\); the program would generate a pseudorandom number in this range, and jump to the corresponding node, where the whole procedure would start afresh.
This algorithm captures a few basic features of free association, but it also misses quite a lot. The model assumes that all destination nodes are equally likely, which is implausible. To accommodate differences in probability, we could give each link \(i\) a weight \(w_i\), then make the probabilities proportional to the weights.
A further complication is that the weights depend on context—on one’s recent history of mental activity. If it weren’t for the combination of Mrs. Robinson and Jackie Robinson, would I have thought of Joe DiMaggio? And now, as I write this, Joltin’ Joe brings to mind Marilyn Monroe, and then Arthur Miller, and I am helpless to stop another whole train of associations. Reproducing this effect in a computer model would require some mechanism for dynamically adjusting the probabilities of entire categories of nodes, depending on which other nodes have been visited lately.
Recency effects of another kind should also be taken into account. The rubber band that repeatedly yanks me back to Simon and Garfunkel and Mrs. Robinson needs to have a place in the model. Perhaps each recently visited node should be added to the list of candidate destinations even if it is not otherwise linked to the current node. On the other hand, habituation is also a possibility: Ideas revisited too often become tiresome, and so they need to be suppressed in the model.
One final challenge: Some memories are not isolated facts or ideas but parts of a story. They have a narrative structure, with events unfolding in chronological order. Nodes for such episodic memories require a next link, and maybe a previous link, too. That chain of links holds your whole life together, to the extent you remember it.
Could a computational model like this one reproduce my mental meanderings? Gathering data for the model would be quite a chore, but that’s no surprise, since it has taken me a lifetime to fill my cranium with that jumble of herbs, Herbs, Simons, Robinsons, and Hoffmans. More worrisome than the volume of data is the fiddly nature of the graph-walking algorithm. It’s easy to say, “Pick a node according to a set of weighted probabilities,” but when I look at the gory details of how it’s done, I have a hard time imagining anything like that happening in the brain.
Here’s the simplest algorithm I know for random weighted selection. It’s not the most efficient such algorithm, but the better methods are even messier. Keith Schwarz has an excellent tutorial and review on the subject. Assume that the data structure representing a node of the network includes a list of links to other nodes and a corresponding list of weights. As shown in the diagram below, the program generates the sequence of cumulative sums of the weights: \(0, w_1, w_1 + w_2, w_1 + w_2 + w_3, \dots\). The next step is to normalize this sequence by dividing each number by the overall sum of the weights. Now we have a sequence of numbers \(p_i\) that increase monotonically from zero to one. Finally, the program selects a random real number \(x\) from the interval \([0, 1)\); \(x\) must lie in one of the normalized intervals \(p_i\), and this value of \(i\) identifies the next node to be selected.
In code—specifically in the Julia programming language—the node selection procedure looks like this:
function select_next(links, weights)
total = sum(weights)
cum_weights = cumsum(weights)
probabilities = cum_weights / total
x = rand()
for i in 1:length(probabilities)
if probabilities[i] >= x
return i
end
end
end
I have slogged through these tedious details of cumulative sums and pseudorandom numbers as a way of emphasizing that the graph-walking algorithm is not as simple as it seems on first glance. And we still haven’t dealt with the matter of adjusting the probabilities on the fly, as attention drifts from topic to topic.
Even harder to fathom is the process of learning—adding new nodes and links to the network. I ended my session of free associating when I came to a question I couldn’t answer: “What’s the Russian for butterfly?” But I can answer it now. The next time I play this game, I’ll add babochka to my list of butterfly terms. In the computational model, inserting a node for babochka is easy enough, but the new node also needs to be linked to all the other butterfly nodes already present. Furthermore, babochka would introduce additional links of its own. It’s phonetically close to babushka (grandmother), one of the few Russian words in my vocabulary. The -ochka suffix is a diminutive, so it needs to be associated with French -ette and Italian -ini. The literal meaning of babochka is “little soul,” which suggests still more associations. Ultimately, learning a single new word might require a full reindexing of an entire tree of knowledge.
Let’s try a different model. Forget about the random walk on a network, with its spaghetti tangle of pointers to nodes. Instead, let’s just try to keep all similar things in the same neighborhood. In the memory banks of a digital computer, that means similar things have to be stored at nearby addresses. Here’s a hypothetical segment of memory centered on the concept dog. The nearby slots are occupied by other words, things, and categories that are likely to be evoked by the thought of dog: the obvious cat and puppy, various breeds of dogs and a few individual dogs (Skippy was the family pet when I was a kid), and some quirkier possibilities. Each item has a numeric address. The address has no intrinsic meaning, but it’s important that all the memory cells are numbered sequentially.
| address | content |
|---|---|
| 19216805 | god |
| 19216806 | the dog that didn’t bark in the night |
| 19216807 | Skippy |
| 19216808 | Lassie |
| 19216809 | canine |
| 19216810 | cat |
| 19216811 | dog |
| 19216812 | puppy |
| 19216813 | wolf |
| 19216814 | cave canem |
| 19216815 | Basset Hound |
| 19216816 | Weimaraner |
| 19216817 | dogmatic |
A program for idly exploring this memory array could be quite simple. It would execute a random walk over the memory addresses, but with a bias in favor of small steps. For example, the next address to be visited might be determined by sampling from a normal distribution centered on the present location. Here’s the Julia code. (The function randn() returns a random real number drawn from the normal distribution with mean \(\mu = 0\) and standard deviation \(\sigma = 1\).)
function gaussian_ramble(addr, 𝜎)
r = randn() * 𝜎
return addr + round(Int, r)
endThe scheme has some attractive features. There’s no need to tabulate all the possible destinations as a preliminary to choosing one of them. Probabilities are not stored as numbers but are encoded by position within the array, and further modulated by the parameter 𝜎, which determines how far afield the procedure is willing to reach in the array. Although the program is still doing some arithmetic in order to sample from a normal distribution, that function could probably be implemented in a simpler way.
But the procedure also has a dreadful defect. In surrounding dog with all of its immediate associates, we leave no room for their associates. The doggy terms are fine in their own context, but what about the cat in the list? Where do we put kitten and tiger and nine lives and Felix? In a one-dimensional array there’s no hope of embedding every memory within its own proper neighborhood.
So let’s shift to two dimensions! By splitting the addresses into two components, we can set up two orthogonal axes. The first half of each address becomes a \(y\) coordinate and the second half an \(x\) coordinate. Now dog and cat are still close neighbors, but they also have private spaces where they can play with their own friends.
However, two dimensions aren’t enough, either. If we try to fill in all the correlatives of The Cat in the Hat, they will inevitably collide and conflict with those of the dog that didn’t bark in the night. Evidently we need more dimensions—a lot more.
Now would be a good moment for me to acknowledge that I am not the first person ever to think about how memories could be organized in the brain. A list of my predecessors might start with Plato, who compared memory to an aviary; we recognize our memories by their plumage, but sometimes we have trouble retrieving them as they flutter about in the cranial cage. The 16th-century Jesuit Matteo Ricci wrote of a “memory palace,” where we stroll through various rooms and corridors in search of treasures from the past. Modern theories of memory tend to be less colorful than these but more detailed, aiming to move beyond metaphor to mechanism. My personal favorite is a mathematical model devised in the 1980s by Pentti Kanerva, who is now at the Redwood Center for Theoretical Neuroscience here in Berkeley. He calls the idea sparse distributed memory, which I’m going to abbreviate as SDM. It makes clever use of the peculiar geometry of high-dimensional spaces.
Think of a cube in three dimensions. If the side length is taken as one unit, then the eight vertices can be labeled by vectors of three binary digits, starting with \(000\) and continuing through \(111\). At any vertex, changing a single bit of the vector takes you to a nearest-neighbor vertex. Changing two bits moves you to a next-nearest-neighbor, and flipping all three bits leads to the opposite corner of the cube—the most distant vertex.
The four-dimensional cube works the same way, with \(16\) vertices labeled by vectors that include all patterns of binary digits from \(0000\) through \(1111\). And indeed the description generalizes to \(N\) dimensions, where each vertex has an \(N\)-bit vector of coordinates. If we measure distance by the Manhattan metric—always moving along the edges of the cube and never taking shortcuts across a diagonal—the distance between any two vertices is simply the number of positions where the two coordinate vectors differ (also known as the Hamming distance). The usual symbol for exclusive OR is ⊕, sometimes called a bun. It reflects the interpretation of the XOR operation as binary addition modulo 2. Kanerva prefers ∗ or ⊗, on the grounds that the role of XOR in high-dimensional computing is more like multiplication than addition. I have decided to duck this controversy by adopting the symbol ⊻, an alternative notation for XOR common among logicians. It’s a modification of ∨, the symbol for inclusive OR. Conveniently, it’s also the XOR symbol in Julia programs.Thus the unit of measure for distance is the bit, and calculating distance is a job for the binary exclusive OR operator (XOR, ⊻), which yields a value of \(1\) for pairs of bits that differ and \(0\) for pairs that are the same:
0 ⊻ 0 = 0
0 ⊻ 1 = 1
1 ⊻ 0 = 1
1 ⊻ 1 = 0
A Julia function for measuring the distance between vertices applies the XOR function to the two coordinate vectors and counts the \(1\)s in the result.
function distance(u, v)
w = u ⊻ v
return count_ones(w)
endAs \(N\) grows large, some curious properties of the \(N\)-cube come into view. Consider the \(1{,}000\)-dimensional cube, which has \(2^{1000}\) vertices. If you choose two of those vertices at random, what is the expected distance between them? Even though this is a question about distance, we can answer it without delving into any geometric details; it’s simply a matter of tallying the positions where the two binary vectors differ. For random vectors, each bit is \(0\) or \(1\) with equal probability, and so the vectors can be expected to differ at half of the bit positions. In the case of a \(1{,}000\)-bit vector, the typical distance is \(500\) bits. This outcome is not a great surprise. What does seem noteworthy is the way all the vertex-to-vertex distances cluster tightly around the mean value of 500.
For \(1{,}000\)-bit vectors, almost all randomly chosen pairs lie at a distance between \(450\) and \(550\) bits. In a sample of \(100\) million random pairs (see graph above) none were closer than \(400\) bits or farther apart than \(600\) bits. Nothing about our life in low-dimensional space prepares us for this condensation of probability in the middle distance. Here on Earth, you might be able to find a place to stand where you’re all alone, and almost everyone else is several thousand miles away; however, there’s no way to arrange the planet’s population so that everyone has this experience simultaneously. But that’s the situation in \(1{,}000\)-dimensional space.
Needless to say, it’s hard to visualize a \(1{,}000\)-dimensional cube, but it’s possible to get a little intuition about the geometry from as few as five dimensions. Tabulated below are all the vertex coordinates of a five-dimensional unit cube, arranged according to their Hamming distance from the origin \(00000\). A majority of the vertices (20 out of 32) are at the middle distances of either two or three bits. The table would have the same shape if any other vertex were taken as the origin.
A serious objection to all this talk of \(1{,}000\)-dimensional cubes is that we’ll never build one; there aren’t enough atoms in the universe for a structure with \(2^{1000}\) parts. But Kanerva points out that we need storage locations only for the items that we actually want to store. We could construct hardware for a random sample of, say, \(10^8\) vertices (each with a \(1{,}000\)-bit address) and leave the rest of the cube as a ghostly, unbuilt infrastructure. Kanerva calls the subset of vertices that exist in hardware hard locations. A set of \(10^8\) random hard locations would still exhibit the same squeezed distribution of distances as the full cube; indeed, this is precisely what the graph above shows.
The relative isolation of each vertex in the high-dimensional cube hints at one possible advantage of sparse distributed memory: A stored item has plenty of elbow room, and can spread out over a wide area without disturbing the neighbors. This is indeed one distinguishing feature of SDM, but there’s more to it.
Conventional computer memory enforces a one-to-one mapping between addresses and stored data items. The addresses are consecutive integers in a fixed range, such as \([0, 2^{64})\). Every integer in this range refers to a single, distinct location in the memory, and every location is associated with exactly one address. Also, each location holds just one value at a time; writing a new value wipes out the old one.
SDM breaks all of these rules. It has a huge address space—at least \(2^{1000}\)—but only a tiny, random fraction of those locations exist as physical entities; this is why the memory is said to be sparse. A given item of information is not stored in just one memory location; multiple copies are spread throughout a region—hence distributed. Furthermore, each individual address can hold multiple data items simultaneously. Thus information is both smeared out over a broad area and smushed together at the same site. The architecture also blurs the distinction between memory addresses and memory content; in many cases, the pattern of bits to be stored acts as its own address. Finally, the memory can respond to a partial or approximate address and find the correct item with high probability. Where the conventional memory is an “exact match machine,” SDM is a “best match machine,” retrieving the item most similar to the requested one.
In his 1988 book Kanerva gives a detailed quantitative analysis of a sparse distributed memory with \(1{,}000\) dimensions and \(1{,}000{,}000\) hard locations. The hard locations are chosen randomly from the full space of \(2^{1000}\) possible address vectors. Each hard location has room to store multiple \(1{,}000\)-bit vectors. The memory as a whole is designed to hold at least \(10{,}000\) distinct patterns. In what follows I’m going to consider this the canonical SDM model, although it is small by mammalian standards, and in his more recent work Kanerva has emphasized vectors with at least \(10{,}000\) dimensions.
Here’s how the memory works, in a simple computer implementation. The command store(X) writes the vector \(X\) into the memory, treating it as both address and content. The value \(X\) is stored in all the hard locations that lie within a certain distance of the address \(X\). For the canonical model this distance is 451 bits. It defines an “access circle” designed to encompass about \(1{,}000\) hard locations; in other words, each vector is stored in about \(1/1{,}000\)th of the million hard locations.
It’s important to note that the stored item \(X\) does not have to be chosen from among the \(1{,}000{,}000\) binary vectors that are addresses of hard locations. On the contrary, \(X\) can be any of the \(2^{1000}\) possible binary patterns.
Suppose a thousand copies of \(X\) have already been written into the SDM when a new item \(Y\) comes along, to be stored in its own set of a thousand hard locations. There might be some overlap between the two sets of locations—sites where both \(X\) and \(Y\) are stored. The later-arriving value does not overwrite or replace the earlier one; both values are retained. When the memory has been filled to its capacity of \(10{,}000\) vectors, each of them stored \(1{,}000\) times, a typical hard location will hold copies of \(10\) distinct patterns.
Now the question is: How can we make sense of this memory mélange? In particular, how can we retrieve the correct value of \(X\) without interference from \(Y\) and all the other items jumbled together in the same storage locations?
The readout algorithm makes essential use of the curious distance distribution in a high-dimensional space. Even if \(X\) and \(Y\) are nearest neighbors among the \(10{,}000\) stored patterns, they are likely to differ by 420 or 430 bits; as a result, the number of hard locations where both values are stored is quite small—typically four, five, or six. The same is true of all the other patterns overlapping \(X\). There are thousands of them, but no one interfering pattern is present in more than a handful of copies inside the access circle of \(X\).
The command fetch(X) should return the value that was earlier written by store(X). The first step in reconstructing the value is to gather up all information stored within the 451-bit access circle centered on \(X\). Because \(X\) was previously written into all of these locations, we can be sure of getting back \(1{,}000\) copies of it. We’ll also receive about \(10{,}000\) copies of other vectors, stored in locations whose access circles overlap that of \(X\). But because the overlaps are small, each of these vectors is present in only a few copies. In the aggregate, then, each of their \(1{,}000\) bits is equally likely to be a \(0\) or a \(1\). If we apply a majority-rule function to all the data gathered at each bit position, the result will be dominated by the \(1{,}000\) copies of \(X\). The probability of getting any result other than \(X\) is about \(10^{-19}\).
The bitwise majority-rule procedure is shown in more detail below, for a toy example of five data vectors of 20 bits each. The output is another vector where each bit reflects the majority of the corresponding bits in the data vectors. (If the number of data vectors is even, ties are broken by choosing \(0\) or \(1\) at random.) An alternative writing-and-reading scheme, also illustrated below, forgoes storing all the patterns individually and instead keeps a tally of the number of \(0\) and \(1\) bits at each position. A hard location has a \(1{,}000\)-bit counter, initialized to all \(0\)s. When a pattern is written into the location, each bit counter is incremented for a \(1\) or decremented for a \(0\). The readout algorithm simply examines the sign of each bit counter, returning \(1\) for positive, \(0\) for negative, and a random value when the counter bit is \(0\).

The two storage schemes give identical results.
From a computer-engineering point of view, this version of sparse distributed memory looks like an elaborately contrived joke. To remember \(10{,}000\) items we need a million hard locations, in which we store a thousand redundant copies of every pattern. Then, in order to retrieve just one item from memory, we harvest data on \(11{,}000\) stored patterns and apply a subtle majority-rule mechanism to unscramble them. And all we accomplish through these acrobatic maneuvers is to retrieve a vector we already had. Conventional memory works with much less fuss: Both writing and reading access a single location.
But an SDM can do things the conventional memory can’t. In particular, it can retrieve information based on a partial or approximate cue. Suppose a vector \(Z\) is a corrupted version of \(X\), where \(100\) of the \(1{,}000\) bits have been altered. Because the two vectors are similar, the command fetch(Z) will probe many of the same sites where \(X\) is stored. At a Hamming distance of 100, \(X\) and \(Z\) can be expected to share about 300 hard locations. Because of this extensive overlap, the vector returned by fetch(Z)—call it \(Z^{\prime}\)—will be closer to \(X\) than \(Z\) is. Now we can repeat the process with the command fetch(Z′), which will return a result \(Z^{\prime\prime}\) even closer \(X\). After only a few iterations the procedure reaches \(X\) itself.
Kanerva shows that this converging sequence of recursive read operations will succeed with near certainty as long as the starting pattern is not too far from the target. In other words, there is a critical radius: Any probe of the memory starting at a location inside the critical circle will almost surely converge to the center, and do so rather quickly. An attempt to recover the stored item from outside the critical circle fails, as the recursive recall process wanders away into the middle distance. Kanerva’s analysis yields a critical radius of 209 bits for the canonical SDM. In other words, if you know roughly 80 percent of the bits, you can reconstruct the whole pattern.
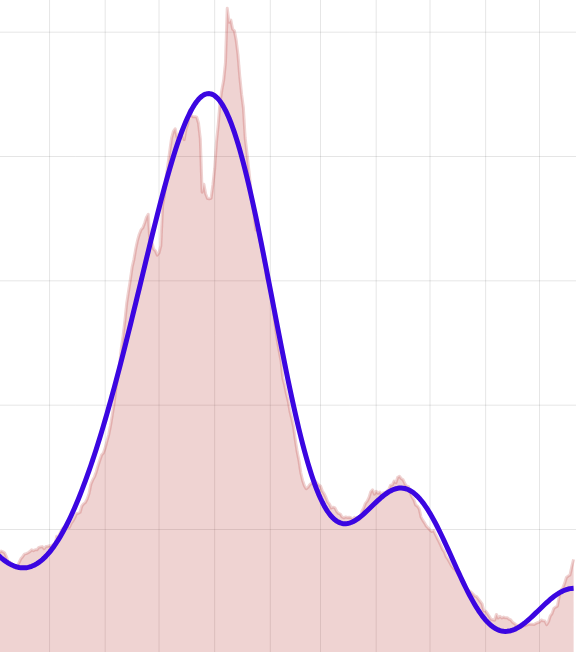
The illustration below traces the evolution of recursive-recall sequences using initial cues that differ from a target \(X\) by \(0, 5, 10, 15 \dots 1{,}000\) bits. In this experiment all sequences starting at a distance of \(205\) or less converged to \(X\) in fewer than \(10\) iterations (blue trails). All sequences starting at a greater initial distance wandered aimlessly through the huge open spaces of the \(1{,}000\)-dimensional cube, staying roughly 500 bits from anywhere.
The transition from convergent to divergent trajectories is not perfectly sharp, as shown in the bad-hair-day graphic below. Here we have zoomed in to look at the fate of trajectories beginning at displacements of \(175, 176, 177, \dots 225\) bits. All trails whose starting point is within 209 bits of the target are colored blue; those starting at a greater distance are red. Most of the blue trajectories converge, quickly going to zero distance, and most of the red ones don’t. Near the critical distance, however, there are lots of exceptions.
The graph below offers yet another view of how initial distance from the target affects the likelihood of eventually converging on the correct memory address. At a distance of \(170\) bits almost all trials succeed; at \(240\) bits almost none do. The crossover point (where success and failure are equally likely) seems to lie at about \(203\) bits, a little lower than Kanerva’s result of \(209\). This discrepancy is not a mystery. Kanerva’s calculation assumes an access circle that encompasses exactly \(1{,}000\) hard locations. My experiments include all hard locations at a distance \(r \le 451\); on average there are \(1{,}070\) such locations.
The ability to reconstruct memories from partial information is a familiar element of human experience. You notice an actor in a television show, and you realize you’ve seen him before, but you don’t remember where. After a few minutes it comes to you: He’s Mr. Bates from Downton Abbey, but without his butler suit. Then there’s the high school reunion challenge: Looking at the stout, balding gentleman across the room, can you recognize the friend you last knew as a lanky teenager in track shorts? Sometimes, filling in the blanks requires a prolonged struggle. I have written before about my own inexplicable memory blind spot for the flowering vine wisteria, which I can name only after patiently working my way through a catalogue of false scents: hydrangea, verbena, forsythia.
Could our knack for recovering memories from incomplete or noisy inputs work something like the recursive recall process with high-dimensional vectors? It’s an attractive hypothesis, but there are also reasons for caution. For one thing, the brain seems to be able to tease meaning out of much skimpier clues. I don’t need to hear four-fifths of the Fifth Symphony before I recognize it; the first four notes will do. A flash of color moving through the trees instantly brings to mind the appropriate species—cardinal, bluejay, goldfinch. A mere whiff of chalkdust transports me back to the drowsy, overheated classroom where I doodled on the desktop all afternoon. These memories are evoked by a tiny fraction of the information they represent, far less than 80 percent.
Kanerva cites another quirk of human memory that might be modeled by an SDM: the tip-of-the-tongue phenomenon, whose essence is that you know you know something, even though you can’t immediately name it. This feeling is a bit mysterious: If you can’t find what you’re looking for, how do you know it’s there? The recursive recall process of the SDM offers a possible answer. When the successive patterns retrieved from memory are getting steadily closer together, you can be reasonably sure they will converge on a target, even before they get there.
In the struggle to retrieve a stubborn fact from memory, many people find that banging on the same door repeatedly is not a wise strategy. Rather than demanding immediate answers—getting bossy with your brain—it’s often better to set the problem aside, go for a walk, maybe even take a nap; the answer may then come to you, seemingly unbidden. Can this observation be explained by the SDM model? Perhaps, at least in part. If a sequence of recalled patterns is not converging, pursuing it further is probably fruitless. Starting over from a nearby point in the memory space might lead to a better outcome. But there’s a conundrum here: How do you find a new point of departure with better prospects? You might think you could just randomly flip a few bits in the input pattern in the hope that you’ll wind up closer to the target, but this is unlikely to work. If a vector is \(250\) bits from the target, then \(750\) bits are already correct (but you don’t know which \(750\) bits); any random change has a \(3/4\) chance of moving farther away rather than closer. To make progress you need to know which way to turn, and that’s a tricky question in \(1{,}000\)-dimensional space.
One aspect of the SDM architecture that seems to match human experience is the effect of repetition or rehearsal on memory. If you repeatedly recite a poem or practice playing a piece of music, you expect to remember it more easily in the future. A computational model of memory ought to exhibit the same training effect. Conventional computer memory certainly does not: There’s no benefit to writing the same value multiple times at the same address. With an SDM, in contrast, each repetition of a pattern adds another copy to all the hard locations within the pattern’s access circle. As a result, there’s less interference from overlapping patterns, and the critical radius for recall is enlarged. The effect is dramatic: When a single extra copy of a pattern is written into the memory, the critical radius grows from about \(200\) bits to more than \(300\).
By the same token, increasing the representation of one pattern can make others harder to recover. This is a form of forgetting, as the heavily imprinted pattern crowds out its neighbors and takes over part of their territory. This effect is also dramatic in the SDM—unrealistically so. A vector stored eight or ten times seems to monopolize most of the memory; it becomes an obsession, the answer to all questions.
A notable advantage of sparse distributed memory is its resilience in the face of hardware failures or errors. I would be unhappy with my own brain if the loss of a single neuron could leave a hole in my memory, so that I could no longer recognize the letter g or remember how to tie my shoelaces. SDM does not suffer from such fragility. With a thousand copies of every stored pattern, no one site is essential. Indeed, it’s possible to wipe out all information stored in \(60\) percent of the hard locations and still get perfect recall of \(10{,}000\) stored items, assuming you supply the exact address as the cue. With partial cues, the critical radius contracts as more sites are lost. After destroying \(60\) percent of the sites, the critical radius shrinks from \(200+\) bits to about \(150\) bits. With \(80\) percent of the sites gone, memory is seriously degraded but not extinguished.
And what about woolgathering? Can we traipse idly through the meadows of sparse distributed memory, serendipitously leaping from one stored pattern to the next? I’ll return to this question.
Most of the narrative above was written several weeks ago. At the time, I was reading about various competing theories of memory, and discussing their merits with my colleagues at the Simons Institute. I wrote up my thoughts on the subject, but I held off publishing because of nagging doubts about whether I truly understood the mathematics of sparse distributed memory. I’m glad I waited.
The Brain and Computation program ended in May. The participants have scattered; I am back in New England, where sage and rosemary are small potted plants rather than burgeoning shrubs spilling over the sidewalk. My morning strolls to the Berkeley campus, a daily occasion for musing about the nature of memory and learning, have themselves become “engrams” stored somewhere in my head (though I still don’t know where to look for them).
I have not given up the quest. Since I left Berkeley I’ve continued reading on theories of memory. I’ve also been writing programs to explore Pentti Kanerva’s sparse distributed memory and his broader ideas on “hyperdimensional computing.” Even if this project fails to reveal the secrets of human memory, it is certainly teaching me something about the mathematical and computational art of navigating high-dimensional spaces.
The diagram below represents the “right” way to implement SDM, as I understand it. The central element is a crossbar matrix in which the rows correspond to the memory’s hard locations and the columns carry signals representing the individual bits of an input vector. The canonical memory has a million rows, each with a randomly assigned \(1{,}000\)-bit address, and \(1{,}000\) columns; this toy version has 20 rows and 8 columns.
The process illustrated in the diagram is the storage of a single input vector in an otherwise empty memory. The eight input bits are compared simultaneously with all \(20\) hard-location addresses. Wherever an input bit and an address bit match—\(0\) with \(0\) or \(1\) with \(1\)—we place a dot at the intersection of the column and the row. Then we count the number of dots in each row, and if the count meets or exceeds a threshold, we write the input vector into the register associated with that row (blue boxes). In the example shown, the threshold is \(5\), and \(8\) of the \(20\) addresses have at least \(5\) matches. In the \(1{,}000\)-bit memory, the threshold would be \(451\), and only about a thousandth of the registers would be selected.
The magic in this design is that all of the bit comparisons—a billion of them in the canonical model—happen concurrently. As a result, the access time for both reading and writing is independent of the number of hard locations, and can be very fast. Circuitry of this general type, known as an associative memory or content-addressable memory, has a role in certain specialized computing applications, such as triggering the particle detectors at the Large Hadron Collider and steering packets through the routers of the internet backbone. And the circuit diagram might also be plausibly mapped onto certain structures in the brain. Kanerva points out that the cerebellum looks a lot like such a matrix. The rows are flat, fanlike Purkinje cells, arranged like the pages of a book; the columns are parallel fibers threaded through the whole population of Purkinje cells. (However, the cerebellum is not the region of the mammalian brain where cognitive memory is thought to reside.)
It would be wonderful to build an SDM simulation based on this crossbar design; unfortunately, I don’t know how to do that with any computer hardware I can lay my hands on. A conventional processor offers no way to compare all the input bits with all the hard-location bits simultaneously. Instead I have to scan through a million hard locations one by one, and at each location compare a thousand pairs of bits. That’s a billion bit comparisons for every item stored into or retrieved from the memory. Add to that the time needed to write or read a million bits (a thousand copies of a \(1{,}000\)-bit vector), and we’re talking about quite a lumbering process. Here’s the code for storing a vector:
function store(v::BitVector)
for loc in SDM
if hamming_distance(v, loc.address) <= r
write_to_register!(loc.register, v)
end
end
end
This implementation needs almost an hour to stock the memory with \(10{,}000\) remembered patterns. (The complete program, in the form of a Jupyter notebook, is available on GitHub.)
Is there a better algorithm for simulating the SDM on conventional hardware? One possible strategy avoids repeatedly searching for the set of hard locations within the access circle of a given vector; instead, when the vector is first written into the memory, the program keeps a pointer to each of the thousand-or-so locations where it is stored. On any future reference to the same vector, the program can just follow the \(1{,}000\) saved pointers rather than scanning the entire array of a million hard locations. The cost of this caching scheme is the need to store all those pointers—\(10\) million of them for the canonical SDM. Doing so is feasible, and it might be worthwhile if you only wanted to store and retrieve exact, known values. But think about what happens in response to an approximate memory probe, with the recursive recall of \(Z^{\prime}\) and \(Z^{\prime\prime}\) and \(Z^{\prime\prime\prime}\), and so on. None of those intermediate values will be found in the cache, and so the full scan of all hard locations is still needed.
Perhaps there’s a cleverer shortcut. A recent review article on “Approximate Nearest Neighbor Search in High Dimensions,” by Alexandr Andoni, Piotr Indyk, and Ilya Razenshteyn, mentions an intriguing technique called locality sensitive hashing, but I can’t quite see how to adapt it to the SDM problem.
The ability to reconstruct memories from partial cues is a tantalizingly lifelike trait in a computational model. Perhaps it might be extended to yield a plausible mechanism for wandering idly through the chambers of memory, letting one idea lead to the next.
At first I thought I knew how this might work. A pattern \(X\) stored in the SDM creates a basin of attraction around itself, where any recursive probe of the memory starting within a critical radius will converge to \(X\). Given \(10{,}000\) such attractors, I can imagine them partitioning the memory space into a matrix of separate compartments, like a high-dimensional foam of soap bubbles. The basin for each stored item occupies a distinct volume, surrounded on all sides by other basins and bumping up against them, with sharp boundaries between adjacent domains. In support of this notion, I would note that the average radius of a basin of attraction shrinks when more content is poured into the memory, as if the bubbles were being compressed by overcrowding.
This vision of what’s going on inside the SDM suggests a simple way to drift from one domain to the next: Randomly flip enough bits in a vector to take it outside the present basin of attraction and into an adjacent one, then apply the recursive recall algorithm. Repeating this procedure will generate a random walk through the set of topics stored in the memory.
The only trouble is, it doesn’t work. If you try it, you will indeed wander aimlessly in the \(1{,}000\)-dimensional lattice, but you will never find anything stored there. The entire plan is based on a faulty intuition about the geometry of the SDM. The stored vectors with their basins of attraction are not tightly packed like soap bubbles; on the contrary, they are isolated galaxies floating in a vast and vacant universe, with huge tracts of empty space between them. A few calculations show the true nature of the situation. In the canonical model the critical radius defining the basin of attraction is about \(200\). The volume of a single basin—measured as the number of vectors inside it—is
$$\sum_{k = 1}^{200} \binom{1000}{k},$$
which works out to roughly \(10^{216}\). Thus all \(10{,}000\) basins occupy a volume of \(10^{220}\). That’s a big number, but it’s still a tiny fraction of the \(1{,}000\)-dimensional cube. Among all the vertices of the cube, only \(1\) out of \(10^{80}\) lies within 200 bits of a stored pattern. You could wander forever without stumbling into one of those basins.
(Forever? Oh, all right, maybe not forever. Because the hypercube is a finite structure, any path through it must eventually become recurrent, either hitting a fixed point from which it never escapes or falling into a repeating cycle. The stored vectors are fixed points, and there are also many other fixed points that don’t correspond to any meaningful pattern. For what it’s worth, in all my experiments with SDM programs, I have yet to run into a stored pattern “by accident.”)
Hoping to salvage this failed idea, I tried a few more experiments. In one case I deliberately stored a bunch of related concepts at nearby addresses (“nearby” meaning within 200 or 300 bits). Within this cluster, perhaps I could skip blithely from point to point. But in fact the entire cluster congealed into one big basin of attraction for the central pattern, which thus became a black hole swallowing up all its companions. I also tried fiddling with the value of \(r\), the radius of the access circle for all reading and writing operations. In the canonical model \(r = 451\). I thought that writing to a slightly smaller circle or reading from a slightly larger one might allow some wiggle room for randomness in the results, but this hope was also disappointed.
All of these efforts were based on a misunderstanding of high-dimensional vector spaces. Trying to find clusters of nearby values in the hypercube is hopeless; the stored patterns are sprinkled much too sparsely throughout the volume. And deliberately creating dense clusters is pointless, because it destroys the very property that makes the system interesting—the ability to converge on a stored item from any point in the surrounding basin of attraction. If we’re going to create a daydreaming algorithm for the SDM, it will have to work some other way.
In casting about for an alternative daydreaming mechanism, we might consider smuggling some graph theory into the world of sparse distributed memory. Then we could take a step back toward the original idea of mental rambling as a random walk on a graph or network. The key to building such graphs in the SDM turns out to be a familiar tool: the exclusive OR operator.
As discussed above, the Hamming distance between two vectors is calculated by taking their bitwise XOR and then counting the \(1\)s in the result. But the XOR operation provides more information than just the distance between two vectors; it also reveals the orientation or direction of the line that joins them. Specifically, the operation \(u \veebar v\) yields a vector that lists the bits that need to be changed to transform \(u\) into \(v\) or vice versa. You might also think of the \(1\)s and \(0\)s in the XOR vector as a sequence of directions to be followed to trace a path from \(u\) to \(v\).
XOR has always been my personal favorite among the Boolean functions. It is a difference operator, but unlike subtraction, XOR is symmetric: \(u \veebar v = v \veebar u\). Furthermore, XOR is its own inverse. This concept is easy to understand with functions of a single argument: \(f(x)\) is its own inverse if \(f(f(x)) = x\), so that applying the function twice gets you back to where you started. For a two-argument function such as XOR the situation is more complicated, but it’s still true that doing the same thing twice restores the original state. Specifically, if \(u \veebar v = w\), then \(u \veebar w = v\) and \(v \veebar w = u\). The three vectors \(u\), \(v\), and \(w\) form a tiny, closed universe. You can apply the XOR operator to any pair of them and you’ll get back the third element of the set. Below is my attempt to illustrate this idea. Each square represents a \(10{,}000\)-bit vector arranged as a \(100\)-by-\(100\) tableau of light and dark pixels. The three patterns appear to be random and independent, but hovering with the mouse pointer will show that each panel is in fact the XOR of the other two. For example, in the leftmost square, each red pixel matches either a green pixel or a blue pixel, but not both.



The self-inverse property suggests a new way of organizing information in the SDM. Suppose the word butterfly and its French equivalent papillon are stored as arbitrary, random vectors. They will not be close together; the distance between them is likely to be about 500 bits. Now we compute the XOR of these vectors, butterfly ⊻ papillon; the result is another vector that can also be stored in the SDM. This new vector encodes the relation English-French. Now we are equipped to translate. Given the vector for butterfly, we XOR it with the English-French vector and get papillon. The same trick works in the other direction.
This pair of words and the relation between them forms the nucleus of a semantic network. Let’s grow it a little. We can store the word caterpillar at an arbitrary address, then compute butterfly ⊻ caterpillar and call this new relation adult-juvenile. What’s the French for caterpillar? It’s chenille. We add this fact to the network by storing chenille at the address caterpillar ⊻ English-French. Now some magic happens: If we take papillon ⊻ chenille, we’ll learn that these words are connected by the relation adult-juvenile, even though we did not explicitly state that fact. It is a constraint imposed by the geometry of the construction.
The graph could be extended further by adding more English-French cognates (dog-chien, horse-cheval) or more adult-juvenile pairs: (dog-puppy, tree-sapling). And there are plenty of other relations to be explored: synonyms, antonyms, siblings, cause-effect, predator-prey, and so on. There’s also a sweet way of linking a set of events into a chronological sequence, just by XORing the addresses of a node’s predecessor and successor.
The XOR method of linking concepts is a hybrid of geometry and graph theory. In ordinary mathematical graph theory, distances and directions are irrelevant; all that matters is the presence or absence of connecting edges between nodes. In the SDM, on the other hand, the edge representing a relation between nodes is a vector of definite length and orientation within the \(1{,}000\)-dimensional space. Given a node and a relation, the XOR operation “binds” that node to a specific position elsewhere in the hypercube. The resulting structure is completely rigid; you can’t move a node without changing all the relations it participates in. In the case of the butterflies and caterpillars, the configuration of four nodes is necessarily a parallelogram, with pairs of opposite sides that have the same length and orientation.
Another distinctive feature of the XOR-linked graph is that the nodes and the edges have exactly the same representation. In most computer implementations of graph-theoretical ideas, these two entities are quite different; a node might be a list of attributes, and an edge would be a pair of pointers to the nodes it connects. In the SDM, both nodes and edges are simply high-dimensional vectors. Both can be stored in the same format.
As a model of human memory, XOR binding offers the prospect of connecting any two concepts through any relation we can invent. But the scheme also has some deficiencies. Many real-world relations are asymmetric; they don’t share the self-inverse property of XOR. An XOR vector can declare that Edward and Victoria are parent and child, but it can’t tell you which is which. Worse, the XOR vector connects exactly two nodes, never more, so a parent of multiple children faces an awkward predicament. Another challenge is keeping all the branches of a large graph consistent with one another. You can’t just add nodes and edges willy-nilly; they must be joined to the graph in the right order. Inserting a pupal stage between the butterfly and the caterpillar would require rewiring most of the diagram, moving several nodes to new locations within the hypercube and recalculating the relation vectors that connect them, all the while taking care that each change on the English side is mirrored correctly on the French side.
Some of these issues are addressed in another XOR-based technique that Kanerva calls bundling. The idea is to create a kind of database by storing attribute-value pairs. An entry for a book might have attributes such as author, title, and publisher, each of which is paired with a corresponding value. The first step in bundling the data is to separately XOR each attribute-value pair. Then the vectors resulting from these operations are combined to form a single sum vector, using the same algorithm described above for storing multiple vectors in a hard location of the SDM. Taking the XOR of an attribute name with this combined vector will extract an approximation to the corresponding value, close enough to identify it by the recursive recall method. In experiments with the canonical model I found that a single \(1{,}000\)-bit vector could hold six or seven attribute-value pairs without much risk of confusion.
Binding and bundling are not mentioned in Kanerva’s 1988 book, but he discusses them in detail in several more recent papers. (See Further Reading, below.) He points out that with these two operations the set of high-dimensional vectors acquires the structure of an algebraic field—or at least an approximation to a field. The canonical example of a field is the set of real numbers together with the operations of addition and multiplication and their inverses. The reals form a closed set under these operations: Adding, subtracting, multiplying or dividing any two real numbers yields another real number (except for division by zero, which is always the joker in the pack). Likewise a set of binary vectors is closed under binding and bundling, except that sometimes the result extracted from a bundled vector has to be “cleaned up” by the recursive recall process in order to recover a member of the set.
Can binding and bundling offer any help when we try to devise a woolgathering algorithm? They provide some basic tools for navigating through a semantic graph, including the possibility of performing a random walk. Starting from any node of an XOR-linked graph, a random-walk algorithm chooses from among all the relations available at that node. Selecting a relation vector at random and XORing it with the address of the node leads to a different node, where the procedure can be repeated. Similarly, in bundled attribute-value pairs, a randomly selected attribute calls forth the corresponding value, which becomes the next node to explore.
But how does the algorithm know which relations or which attributes are available for choosing? The relations and attributes are represented as vectors and stored in the memory just like any other objects, but there is no obvious means of retrieving those vectors unless you already know what they are. You can’t say to the memory, “Show me all the relations.” You can only present a pattern and ask, “Is this vector present? Have you seen it or something like it?”
With a conventional computer memory, you can do a core dump: Step through all the addresses and print out the value found at each location. There’s no such procedure for a distributed memory. I learned this troubling fact the hard way. While building a computational model of the SDM, I got the pieces working well enough that I could store a few thousand randomly generated patterns in the memory. But I could not retrieve them, because I didn’t know what to ask for. The solution was to maintain a separate list, outside the SDM itself, keeping a record of everything I stored. But it seems farfetched to suppose that the brain would maintain both a memory and an index to that memory. Why not just use the index, which is so much simpler?
In view of this limitation, it seems that sparse distributed memory is equipped to serve the senses but not the imagination. It can recognize familiar patterns and store novel ones, which will then be recognized when next encountered, even from partial or corrupted cues. With binding or bundling, the memory can also keep track of relations between pairs of stored items. But whatever is put into the memory can be gotten out only by supplying a suitable cue.

When I look at the publicity poster for The Graduate, I see Dustin Hoffman, more leery than leering, regarding the stockinged leg of Anne Bancroft, who plays Mrs. Robinson. This visual stimulus excites several subsets of neurons in my cerebral cortex, corresponding to my memories of the actors, the characters, the story, the soundtrack, the year 1967. All of this brain activity might be explained by the SDM memory architecture, if we grant that subsets of neurons can be represented in some abstract way by long, random binary vectors. What’s not so readily explained is how I can summon to mind all the same sensations without having the image in front of me. How do I draw those particular long, random sequences out of the great tangle of vectors without already knowing where they are?
So ends my long ramble, on a note of doubt and disappointment. It’s hardly surprising that I have failed to get to the bottom of it all. These are deep waters.
On the very first day of the Simons brain-and-computation program, Jeff Lichtman, who is laboring to trace the wiring diagram of the mouse brain, asked whether neuroscience has yet had its Watson-Crick moment. In molecular genetics we have reached the point where we can extract a strand of DNA from a living cell and read many its messages. We can even write our own messages and put them back into an organism. The equivalent capability in neuroscience would be to examine a hunk of brain tissue and read out the information stored there—the knowledge, the memories, the world view. Maybe we could also write information directly into the brain.
Science is not even close to achieving this feat—to the great relief of many. That includes me: I don’t look forward to having my thoughts sucked out of my head through electrodes or pipettes, to be replaced with #fakenews. However, I really do want to know how the brain works.
The Simons program left me dazzled by recent progress in neuroscience, but it also revealed that some of the biggest questions remain wide open. The connectomics projects of Lichtmann and others are producing a detailed map of millions of neurons and their interconnections. New recording techniques allow us to listen in on the signals emitted by individual nerve cells and to follow waves of excitation across broad regions of the brain. We have a pretty comprehensive catalogue of neuron types, and we know a lot about their physiology and biochemistry. All this is impressive, but so are the mysteries. We can record neural signals, but for the most part we don’t know what they mean. We don’t know how information is encoded or stored in the brain. It’s rather like trying to understand the circuitry of a digital computer without knowing anything of binary arithmetic or Boolean logic.
Pentti Kanerva’s sparse distributed memory is an attempt to fill in some of these gaps. It is not the only such attempt. A better-known alternative is John Hopfield’s conception of a neural network as a dynamical system settling into an energy-minimizing attractor. The two ideas have some basic principles in common: Information is scattered across large numbers of neurons, and it is encoded in a way that would not be readily understood by an outside observer, even one with access to all the neurons and the signals passing between them. Schemes of this kind, essentially mathematical and computational, occupy a conceptual middle ground between high-level psychology and low-level neural engineering. It’s the layer where the meaning is.
Further Reading
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences 79(8):2554–2558.
Kanerva, Pentti. 1988. Sparse Distributed Memory. Cambridge, Mass.: MIT Press.
Kanerva, Pentti. 1996. Binary spatter-coding of ordered K-tuples. In C. von der Malsburg, W. von Seelen, J. C. Vorbruggen and B. Sendhoff, eds. Artificial Neural Networks—ICANN 96 Proceedings, pp. 869–873. Berlin: Springer.
Kanerva, Pentti. 2000. Large patterns make great symbols: An example of learning from example. In S. Wermter and R. Sun, eds. Hybrid Neural Systems, pp. 194–203. Heidelberg: Springer. PDF
Kanerva, Pentti. 2009. Hyperdimensional computing: An introduction to computing in distributed representation with high-dimensional random vectors. Cognitive Computation 1(2):139–159. PDF
Kanerva, Pentti. 2010. What we mean when we say “What’s the Dollar of Mexico?”: Prototypes and mapping in concept space. Report FS-10-08-006, AAAI Fall Symposium on Quantum Informatics for Cognitive, Social, and Semantic Processes. PDF
Kanerva, Pentti. 2014. Computing with 10,000-bit words. Fifty-second Annual Allerton Conference, University of Illinois at Urbana-Champagne, October 2014. PDF
Plate, Tony. 1995. Holographic reduced representations. IEEE Transactions on Neural Networks 6(3):623–641. PDF
Plate, Tony A. 2003. Holographic Reduced Representation: Distributed Representation of Cognitive Structure. Stanford, CA: CSLI Publications.
Rahimi, Abbas, Sohum Datta, Denis Kleyko, E. Paxon Frady, Bruno Olshausen, Pentti Kanerva, and Jan M. Rabaey. 2017. High-dimensional computing as a nanoscalable paradigm. IEEE Transactions on Circuits and Systems 64(9):2508–2521. Preprint PDF
Responses from readers:
Please note: The bit-player website is no longer equipped to accept and publish comments from readers, but the author is still eager to hear from you. Send comments, criticism, compliments, or corrections to brian@bit-player.org.
Publication history
First publication: 31 July 2018
Converted to Eleventy framework: 22 April 2025


Out of my depth here, but seems like some of this may relate to the interesting, commonplace “tip-of-the-tongue” phenomenon (I studied it a bit in the 1970s, but haven’t kept up with research), wherein a person can’t quite think of a word they want, but can think of the beginning or middle letters, or the the number of syllables, or a sound-alike word, or synonymous words… they’re dabbling all around it in their ‘memory-bank’ but with difficulty specifically retrieving it.
In turn, the whole universal phenomenon of simply speaking a proper sentence — rapidly, spontaneously drawing forth from memory the right words in the right order — that we all do all the time — seems incomprehensible! In linguistic terms, any of us is capable of producing, at any moment, a unique sentence that has never before been uttered in history, and likely never will be again.
[But maybe I'm taking you too far afield getting into speech production and processing; you have enough to deal with already!]
The next time you’re trying to identify some shrub, trust Shakespeare: “There’s rosemary, that’s for remembrance” (Hamlet) Whatever it is you’re trying to remember, it’s probably rosemary.(Applying this method to learning foreign words for “butterfly” is left as an exercise.)
Ahhh, I see now you DID make brief mention of the tip-of-the-tongue phenomena in a paragraph I somehow missed before. Duhhh! It comes right after a very brief mention of another phenomena that fascinates me: how we are able to hear just 2 or 3 notes of a melody (say, while scanning through radio channels in the car) and immediately know the specific song and musicians playing it (or similarly, as you also mention, just a whiff of a certain smell will take one back to a very specific moment or event in time). No doubt there’s some sort of algorithmic explanation, though when it happens it feels almost mystical!
A little off topic, but it would be interesting to read a post where you compare your impressions of Berkeley and Cambridge. What do you like and dislike about each city?
The XOR network of concepts reminded me, maybe superficially, of the discovery of linear relation between vector embeddings in the wordvec paper (page 4). If we denote the vector for a word by the word itself, we have approximate equalities such as China - Beijing = Spain - Madrid. The difference could be said to represent the relation <capital-of>. There is a post that attempts to explain these properties (section: “Why do Semantic Relations correspond to Directions?”).
Regarding your assertion that the algorithm for choosing the next path in a random walk by weighted sum being “not simple”, there is actually a very simple way to achieve it: if the next node list allows duplicates (ie the graph allows more than one edge between same nodes) then every link can have weight 1.0 and the choice can be completely random yet still act as if weighted: the associations learned more than once simply have more chances to be picked.
I actually started with this design - for a Markov chat bot when I was a novice programmer - and only came to the weighted sum version as an optimization of the equally weighted with duplicates version. Also, even then there is a simple implementation: if you memoize the sum of weights and keep it updated as links are added, then selecting a path can be done by the following: first, choose a random float between 0 and total_sum. Second, loop over the list in order adding each weight to an accumulator register, stopping when the next weight would put the accumulator > total_sum. The node you are at is the next one to take, picked with weighted probability. Think of it as painting a number line with segments of size according to target weight and throwing a dart. Note how this is a natural transformation of the equal weight with duplicates algorithm: they both have equal target areas just the equal weights with duplicates has many 1.0 width segments mixed up in the list, while the optimization gathers them into blocks and then in effect applies run length encoding.
Perhaps most interesting is that I also tried a 3rd way to implement the chat bot which was equal weights with no duplicates. (So that seeing a word pairing many times would not learn anything new to seeing it once). Interestingly this performed as well as, if not better, in subjective tests as to how “good” the conversations resulted AND it still appeared to learn in a way that would seem impossible to explain given the lack of updating weights. What happens is that even though it can’t learn new information beyond the 1.0 weight at a word to word level, overall if it encounters certain common phrases repeated slightly differently in different sentences then I believe this forms graph structures which turn those phrases into basins of attraction anyway. Thus the frequency of common words and phrases was still common in the generated output because the common patterns had more chances for the random walk to enter that part of the graph.
To amplify my final point in my previous comment: what I am saying is that a naive weighted sum may actually over represent the probability an edge should be picked, because certain words/phrases get to “double dip”: they have a high weight because they are common and they live in subgraphs with many indegrees.
As a concrete example, once my naively weighted Markov chat bots learned the common sub-phrase “had had” it was all over for realism: generated texts would be full of sentences containing “had had had” and “had had had had”. This can be mitigated by going to an order-2 Markov model, but I argue that that only kicks the over-representation problem up one level.
I don’t see why you can’t put your relations in there, too.
They’re all related to one another by being in the set of relations. And of course each can have a set of other properties, like symmetry / anti-symmetry, one-to-one / many-to-one / one-to-many, containing vs. membership, transitive, associative, what-have-you.
You might think you still need a key for relations, but really anything that gets you in is not more than two steps away from the set of relations, providing it has any properties at all (which is a relation). In life there’s no such thing as “no stimulus” — that’s a stimulus, too — so you don’t need a special way in.
elements (case, binding).