American Scientist
November-December 1996
Computing Science
Machine Politics
Brian Hayes
Reapportionment and redistricting are vexing problems of meta-politics. They are "meta" issues because they concern the rules of the political process itself--the way the teams are chosen. In the American political system, a decision about reapportionment and redistricting helps determine who will make all other decisions for the next 10 years. It's no surprise, then, that disputes over these matters have often been rancorous. The first Presidential veto in American history (handed down by Washington in 1792) rejected a Congressional reapportionment plan. By the 1920s the reapportionment issue had become so contentious that the decade ended before Congress could agree on a new formula. More recently, hundreds of redistricting plans have been challenged in court; two Supreme Court decisions last summer invalidated Congressional districts in North Carolina and Texas.
This history of bitter conflict prompts speculation on the meta-meta-political question of how best to resolve meta- political questions. In particular: Would it be feasible to take the process out of politics--indeed to take it out of human hands altogether? The answer is surely yes. Computer programs could readily draw legislative districts. Drawing good districts, however, is a more challenging assignment. And harder still would be persuading the legal and political establishment to give up control of the process and accept an algorithmic solution.
Whether or not computerized redistricting would make for good government, it offers some interesting exercises in mathematics and computer science. Algorithms for redistricting exploit techniques from computational geometry, graph theory, combinatorics and optimization methods. Even if such algorithms are never embodied in law, perhaps they can suggest some ideas that would be useful in a more conventional approach to redistricting.
Remaking the House
The U.S. House of Representatives reconstitutes itself every 10 years in a two-part process. The first part is reapportionment, in which each state is allotted its share of representatives. This is a purely arithmetical operation, and at first it appears quite simple. Each state's share of the seats in the House is proportional to its share of the total population, as enumerated in the decennial census. But representatives come only in integer units, and so some rounding of numbers is needed. That's where the trouble lies. There are many schemes for rounding, some of which favor the larger states and some the smaller.
From 1790 until 1940, reapportionment was a reliable source of Congressional acrimony every 10 years. Since 1941, remarkably, it has become a nonissue. What made the difference was writing an algorithm into the law and thereby making the reapportionment process automatic. Once the census returns are in, the allocation of seats to states is immediately determined just by cranking the numbers through the algorithm. There is no room for human judgment or discretion. As it happens, the algorithm chosen is probably not the best one for the purpose, but no major faction has been sufficiently disgruntled to mount a serious challenge. This absence of discord is perhaps the one bit of empirical evidence suggesting that algorithmic methods might really have something to offer to political science.
The second part of the decennial legislative makeover is redistricting. Once a state learns that it will have k seats in Congress, it must divide its territory into k districts, each of which will elect one member. This is not an arithmetic procedure but a geometric one, and it is severely underconstrained. For any k > 1, there are many, many ways of drawing lines on the map to create k districts. This superabundance of solutions is an invitation to political (or meta-political) mischief.
The kind of mischief that comes to mind first is the partisan gerrymander--a redistricting plan that favors one political party over another. The term dates back to 1812, when Elbridge Gerry, as governor of Massachusetts, presided over the creation of a sinuous legislative district that opponents compared to a salamander. There is also the "sweetheart" gerrymander, where incumbents of opposing parties collude on a redistricting plan to ensure their own re-election. Political gerrymandering is roundly condemned by civic-interest groups, who argue that it gives an unfair advantage to those who happen to be in control in a year divisible by 10. They get to rig the electoral machinery to retain their advantage throughout the following decade.
The legal status of political gerrymandering is uncertain. No federal statute explicitly forbids it, and so far the Supreme Court has never overruled a districting plan because of political bias. Nevertheless, gerrymandering is widely considered unsporting, and blatant instances are likely to offend the electorate.
Another form of gerrymandering, which aims to dilute the political strength of racial and ethnic minorities, was outlawed by the Voting Rights Act of 1965. Measures taken to comply with this act were the issue in the recent North Carolina and Texas litigation. Both states, under instruction from the Department of Justice, created "minority-majority districts" where African-American or Hispanic communities would be able to elect representatives of their choice. The Supreme Court ruled four of these districts unconstitutional on the grounds that race or ethnicity had been the predominant consideration in drawing them. (Note: I live and vote in the soon-to-be-former 12th district of North Carolina, and the recent commotion over its status is what inspired me to write on this theme. North Carolina districts serve as examples in much of the discussion that follows.)
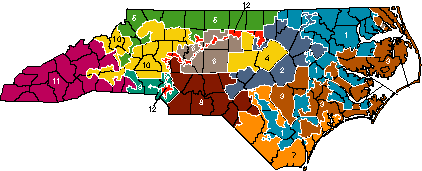
Figure 1. North Carolina's 12 Congressional districts will soon be redrawn to comply with a court order. The state's 1990 population of 6,628,637 yields an ideal district size of 552,386, which the existing districts match almost exactly. Map copyright 1992, Institute of Government, University of North Carolina at Chapel Hill.
The Good District
There is no consensus on what qualities a good redistricting plan ought to have, but here are some widely recognized desiderata:
- All the districts within a state should be equal in population. This is the burden of the "one person, one vote" rule enunciated in a series of Supreme Court decisions beginning with Baker v. Carr in 1962. The court has enforced a remarkably stringent standard of numerical exactness; in 1983 a New Jersey plan was struck down for numerical inequities of 0.69 percent. (For comparison, the error in the 1990 census is estimated at 1.4 percent, and from state to state the average population of a Congressional district varies by almost 60 percent.)
- Each district should be a single contiguous territory. At least some states accept the minimal definition of contiguity, allowing regions connected by a single point. There are two places in North Carolina where districts cross each other, which implies that the connecting isthmus must be a dimensionless point.
- Districts should be compact. Tentacles wriggling across the landscape arouse suspicions, including those of Supreme Court justices. (The North Carolina 12th district is 165 miles long but so narrow that a candidate for the seat remarked, "I can drive down Interstate 85 with both car doors open and hit every person in the district.") Compactness is surprisingly tricky to define and measure. Computational geometry might seem to offer guidance here, but H. Peyton Young of the University of Maryland has shown that various mathematical measures of compactness yield counterintuitive results. For example, a spiral tract of land that winds around itself like a coiled snake passes several tests of compactness, but few would consider it a natural shape for a Congressional district.
- Districts should recognize existing communities of interest. This is an argument for homogeneity, for creating districts that are uniformly urban or rural, coastal or mountainous, industrial or agrarian, etc.
- Similarly, districts should conform to established natural and political boundaries whenever possible. Until 1990 North Carolina districts were always assembled from whole counties, but that practice has had to yield to other imperatives.
- Stability and continuity are virtues in a redistricting plan. A procedure that starts from scratch and draws an entirely new map every decade is likely to be unpopular not only with incumbents but also with constituents.
- Finally, under the Voting Rights Act a district must not be drawn with the intent or the effect of excluding minority candidates from election.
Conflicts between these criteria are commonplace. Creating minority-majority districts may require splitting counties; and the one-person, one-vote rule can put all the other factors in jeopardy. When compromise is necessary, the courts have given the highest precedence to numerical equality.
Point-and-Click Redistricting
The computer is already an essential tool in redistricting; no state today draws its districts with Magic Markers. The computer tools in common use are interactive programs. You sit at a display screen showing a state map that can zoom in on individual counties, precincts or census tracts. You select a geographic unit on the screen and then issue a command to assign it to a district or transfer it from one district to another. The system offers immediate feedback on the political and demographic consequences of each move. You see at a glance the population of each district, its racial and ethnic composition and various indicators of political allegiance.
Underlying this interactive facility is a database linked to the map. Basic demographic data come from the Census Bureau, with populations broken down into geographic units as small as the census block, which generally comprises about a dozen houses. Political intelligence-such as numbers of registered voters, party affiliations, voter turnout statistics and the results of key elections-has to be collected from county boards of elections. The hardest part of building the database is reconciling data from different sources. Boundaries of wards and precincts don't necessarily coincide with the boundaries of census blocks, and so interpolation is needed. (For the 2000 census, the states and the Census Bureau are cooperating to make the boundaries more consistent, which means the next census should be a more efficient tool for the gerrymanderer.)
The introduction of computers into the redistricting process has allowed more precise analysis of proposed plans. A map can be fine-tuned by shifting individual census blocks from one district to another, whether to equalize populations or to achieve political goals. It is no accident that in many states both major parties have access to their own computer systems for redistricting.
For the 1990 round of redistricting most states employed proprietary software specially designed for the purpose and running on mainframes or minicomputers. For the 2000 round there is growing interest in adapting more versatile geographic information systems to redistricting, and running them on client-server networks of computers. But these systems too are mere interactive aids to the human redistricter; they do not make autonomous decisions about where to draw boundary lines.
Algorithmic Redistricting
In the 1960s there was a brief flurry of interest in automated redistricting. This was at a time when the electronic computer was still a novel and oracular machine, widely viewed as a kind of magical question-answering and problem-solving service. Even so, algorithmic methods met with resistance or indifference, and they were used in only a few small-scale demonstration projects.
One of the more sophisticated redistricting algorithms was devised by James B. Weaver and Sidney W. Hess of Atlas Chemical Industries in Delaware. They based their approach on a problem in operations research: If you want to build a number of warehouses (or telephone switching centers, or pizza shops) to serve a dispersed population of customers, where are the best places to put them? Methods for answering this question are mainly iterative; they work by progressive refinement of an initial guess, converging on a solution that minimizes the sum of the distances from each warehouse to all the customers in its territory. In the redistricting case the actual warehouse locations are not of interest; it is the territories surrounding them that the algorithm is meant to calculate. The method puts heavy emphasis on compactness.
Henry F. Kaiser of the University of Wisconsin and Stuart Nagel of the University of Illinois developed another early redistricting program. It does not create a map de novo but instead works to improve an existing map by shifting population units from one district to another. A district can either give away a unit, or else two neighboring districts can swap units. In either case, the change is accepted only if it improves population equality (or some other measure of the plan's fitness). The Kaiser- Nagel procedure is a "steepest-descent" algorithm. It works like a marble rolling over a hummocky landscape, always moving downhill. The principal weakness of such schemes is that the marble can get stuck in a local trough and never find the global optimum-the lowest point on the entire landscape.
A few state legislative districts were drawn by computer programs in Iowa in 1967 and in Delaware in 1968. As far as I know, computer-automated redistricting has not been given a serious trial since then.
Do-It-Yourself Redistricting
Lately I have tried implementing a few elementary redistricting algorithms, testing them on North Carolina examples. My toy geographic information system includes county-level demographic data (downloaded from the Census Bureau Web site), a polygonal outline of each county (using coordinates cadged from a commercial Postscript map), and a hand-compiled "touch list" of contiguity data. (No political information is included.) Maps drawn by this system cannot be taken seriously as redistricting proposals, in part because whole counties are too coarse a unit of population to satisfy the requirements of district equality and the Voting Rights Act. But even a crude model reveals some of the traps and snares that always await when you try to specify a process in enough detail for a machine to do it. (Source code is available.)
The simplest of the algorithms is a cake-cutting method. Imagine holding a knife over a map of North Carolina, with the blade lined up north-to-south as it moves slowly from west to east. As soon as the knife has crossed counties with enough people to make up a Congressional district, you cut. Then the knife continues westward, until it has passed over another district's worth of population, where you make a second cut, and so on. The procedure creates a series of districts as vertical slices. A variation of the method was once the subject of a proposed ballot initiative in California.
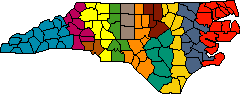
Figure 2. Cake-cutting algorithm sweeps across the state from west to east. Using counties as indivisible units of population, the method yields district populations with a mean deviation of 11.8 percent.
In describing an algorithm like this one, details are crucial. When is the knife blade deemed to have passed over a county-when it touches the westernmost point, the easternmost, the midpoint, the county seat? How do you adjudicate ties, when two or more counties lie at the same longitude? Exactly when does the knife blade cut off a group of counties-just before the district exceeds the ideal size, or just after, or by some other rule? Decisions on these matters may be arbitrary, but they have to be stated explicitly.
Maintaining contiguity in the districts turns out to be the trickiest part of writing a program for the cake-cutting algorithm. Just because two counties are adjacent in a list sorted in west-to-east order does not mean the counties are contiguous. I dealt with this complication as I was writing the program, but a subtler problem caught me by surprise later, when I first tested it. The procedure can run into a blind alley, leaving a county stranded among counties already allocated to other districts. In this situation the program simply fails: It cannot create the required k contiguous districts.
Using counties as indivisible units of population, the cake-cutting algorithm yields pretty ragged-looking districts, with a mean deviation from the ideal district size of almost 12 percent. If the same algorithm were applied to census blocks, the results would be much smoother (North Carolina has 100 counties, compared with almost 230,000 census blocks), but some of the districts would be very long and skinny.
Another model for a redistricting algorithm is the National Football League draft, where the team with the worst win- loss record gets to choose first from the pool of new players. In the redistricting version of the draft, the district with the smallest population chooses from the pool of unclaimed counties, always picking the highest-population county contiguous to its own territory. (In the argot of computer science this is a "greedy algorithm.") Again, details such as the handling of ties need careful attention. Also, getting the procedure started is a potential trouble spot. The obvious strategy is to begin with empty districts, so that the k largest counties will be selected as the "nuclei" of k Congressional districts. This happens to work reasonably well in North Carolina, but it is easy to imagine pathological cases where all the largest counties are in a tight cluster, producing severely deformed districts.
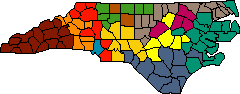
Figure 3. Greedy algorithm grows districts by repeatedly adding to each one of them the largest district contiguous to its territory. The mean population deviation of the plan shown is 10.1 percent.
A glance at the output of either the cake-cutting or the greedy algorithm shows immediate opportunities for improving the map. Shifting or swapping selected counties would help to equalize populations or make the districts more compact. This suggests adding a post-processing stage to optimize the alignments. The Kaiser-Nagel algorithm is just such a procedure, and so I wrote a program based on similar principles, using population equality as the function to be optimized. Single-county moves were attempted repeatedly, in a specific sequence, until the system reached a stable state, where no further move would improve the situation. Applied to the output of the greedy algorithm, the program reduced the mean deviation from 10.1 percent to 4.4 percent.
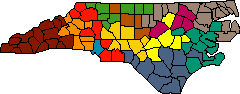
Figure 4. Steepest-descent optimization improves on the greedy algorithm by shifting counties between districts whenever a move yields a better population balance. The mean deviation is 4.4 percent.
As noted above, the Kaiser-Nagel procedure is a steepest-descent method, and therefore vulnerable to getting trapped in a local optimum. A technique called simulated annealing can overcome this drawback. The idea is to accept not only all moves that improve population equality but also a few randomly selected detrimental moves. In other words, when a county is shifted from one district to another, the move is always accepted if it yields better population balance, and in addition it may sometimes be accepted even if it makes the balance worse. The probability of accepting an unfavorable move is determined by a parameter analogous to a temperature, and the system is "annealed" by steadily reducing the temperature toward zero, where only favorable moves are possible. The effect is to jiggle the system out of premature local optima, increasing the chance that it will eventually find the global optimum.
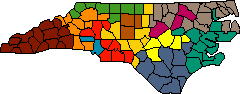
Figure 5. Simulated annealing allows occasional detrimental moves, as a strategy to avoid getting stuck in a local optimum inferior to the global one. Mean deviation is reduced to under 1 percent.
In my first attempt at an annealing program I was again caught off-guard by contiguity problems. I had not foreseen something that now seems obvious: that giving away a county can leave a district in two or more disconnected pieces. When this bug was corrected, the program worked quite well. The best run in a series of experiments with various annealing schedules produced a mean population deviation of under 1 percent. But this improvement comes at a high price: The algorithm is no longer deterministic. Because the program has an element of randomness, repeated runs on the same input data yield different results. This is a loophole the gerrymanderer could exploit, running the program again and again until the result looks "right."
Beyond Human Control
When computer-aided redistricting was first talked about 30 years ago, it was supposed to end political gerrymandering. So far, it has mainly had the opposite effect, providing a better tool for the manipulation and coordination of political data. As computers and software systems grow more powerful, gerrymandered districts will doubtless become both more effective and more subtly hidden.
The algorithmic approach offers an alternative, but it would require a major shift in attitude and expectations--a meta- political revolution. No longer would redistricting be an opportunity to seize political advantage; it would have to be seen as a neutral or arbitrary event, beyond human control, above politics, subject to luck, much like the random choice of which candidate's name is listed first on a ballot. Redistricting would also be lost as an instrument for achieving social goals, such as creating a more racially balanced Congress.
If algorithmic redistricting is not to become another form of high-tech gerrymandering, the mandated algorithm would have to be spelled out in exacting detail, leaving no discretion to the programmer or the operator of the computer. The specification of the algorithm would also have to be openly published, presumably as part of a statute, so that anyone could write a program to check on the result of the official computation. And the specification would have to be so explicit and detailed that every correct implementation of the algorithm would give identical results on all legal inputs.
Legislators have little experience writing algorithmic specifications. Even for experts, creating a correct and ambiguity-free definition of a practical redistricting algorithm would be a daunting challenge. Of necessity, the algorithm would have to be a simple one. Elaborate weighing and balancing of multiple criteria, or complicated hints and heuristics, would leave too much room for mistakes and mischief. Also, the algorithm would have to be deterministic, so that it would always yield the same result on the same input data. And the required inputs themselves would have to be simple and trusted, perhaps limited to what the Census Bureau supplies.
After a few weeks of experimenting with redistricting algorithms, am I prepared to turn the nation's political map over to computers? I'm unsure. There is no doubt that people can draw much better districts than any simple program can. Unfortunately, people can also draw much worse districts. Thus the question of whether we would be better off with people or machines drawing district lines depends on one's assessment of the intentions and character of the people or the machines who would do the drawing.
Bibliography
Balinsky, Michel L., and H. Peyton Young. 1982. Fair Representation: Meeting the Ideal of One Man, One Vote. New Haven: Yale University Press.
Balinsky, M. L., and H. P. Young. 1985. The apportionment of representation. In Proceedings of Symposia in Applied Mathematics, Vol. 33. Providence: American Mathematical Society.
Butler, David, and Bruce Cain. 1992. Congressional Redistricting: Comparative and Theoretical Perspectives. New York: Macmillan Publishing.
Cain, Bruce E. 1984. The Reapportionment Puzzle. Berkeley: University of California Press.
Congressional Quarterly, Inc. 1990. Jigsaw Politics: Shaping the House After the 1990 Census. Washington, D.C.: Congressional Quarterly, Inc.
Kaiser, Henry F. 1966. An objective method for establishing legislative districts. Midwest Journal of Political Science, X (May).
Nagel, Stuart S. 1965. Simplified bipartisan computer redistricting. Stanford Law Review 17:863-899.
O'Hare, William P. 1989. Redistricting in the 1990s: A Guide for Minority Groups. Washington, D.C.: Population Reference Bureau.
O'Rourke, Terry B. 1972. Reapportionment: Law, Politics, Computers. Washington, D.C.: American Enterprise Institute for Public Policy Research.
Orr, Douglas Milton, Jr. 1970. Congressional Redistricting: The North Carolina Experience.
Roeck, Ernest C., Jr. 1961. Measuring compactness as a requirement of legislative apportionment. Midwest Journal of Political Science V (February 1961): 70-74.
U.S. Bureau of the Census: http://www.census.gov/.
Weaver, James B. 1970. Fair and Equal Districts: A How-to-Do-It Manual on Computer Use. New York: National Municipal League.
Weaver, James B., and Sidney Hess. 1963. A procedure for nonpartisan districting: developments of computer techniques. Yale Law Journal 73:288-308.
Young, H. P. 1988. Measuring the compactness of legislative districts. Legislative Studies Quarterly 13, No. 1 (February): 105-116.
© 1996 Brian Hayes